Two particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
To solve the problem of finding the separation between two particles thrown horizontally in opposite directions when their velocities are perpendicular to each other, we can follow these steps:
Step 1: Understand the Motion
Two particles are thrown horizontally from the same height h with velocities u1=4m/s and u2=3m/s in opposite directions. We need to find the time t when their velocities become perpendicular.
Step 2: Determine the Velocity Components
For particle 1 (thrown with u1=4m/s):
- Horizontal velocity: v1x=4m/s
- Vertical velocity: v1y=−gt (downward direction)
For particle 2 (thrown with u2=3m/s):
- Horizontal velocity: v2x=−3m/s
- Vertical velocity: v2y=−gt (downward direction)
Step 3: Condition for Perpendicular Velocities
The velocities are perpendicular when the dot product of their velocity vectors is zero:
v1⋅v2=0
This means:
(4^i−gt^j)⋅(−3^i−gt^j)=0
Calculating the dot product:
4⋅(−3)+(−gt)⋅(−gt)=−12+g2t2=0
Thus, we have:
g2t2=12
t2=12g2
t=√12g=2√3g
Step 4: Calculate the Horizontal Distances
Now we calculate the horizontal distances traveled by each particle when t=2√3g:
- Distance traveled by particle 1:
d1=u1⋅t=4⋅2√3g=8√3g
- Distance traveled by particle 2:
d2=u2⋅t=3⋅2√3g=6√3g
Step 5: Calculate the Separation
The total separation S between the two particles when their velocities are perpendicular:
S=d1+|d2|=8√3g+6√3g=14√3g
Step 6: Substitute the Value of g
Assuming g≈10m/s2:
S=14√310≈2.42m
Thus, the separation between the two particles when their velocities are perpendicular is approximately 2.42m.
---
Two particles are thrown horizontally from the same height h with velocities u1=4m/s and u2=3m/s in opposite directions. We need to find the time t when their velocities become perpendicular.
For particle 1 (thrown with u1=4m/s):
- Horizontal velocity: v1x=4m/s
- Vertical velocity: v1y=−gt (downward direction)
- Horizontal velocity: v2x=−3m/s
- Vertical velocity: v2y=−gt (downward direction)
The velocities are perpendicular when the dot product of their velocity vectors is zero:
v1⋅v2=0
This means:
(4^i−gt^j)⋅(−3^i−gt^j)=0
Calculating the dot product:
4⋅(−3)+(−gt)⋅(−gt)=−12+g2t2=0
Thus, we have:
g2t2=12
t2=12g2
t=√12g=2√3g
Now we calculate the horizontal distances traveled by each particle when t=2√3g:
- Distance traveled by particle 1:
d1=u1⋅t=4⋅2√3g=8√3g
- Distance traveled by particle 2:
d2=u2⋅t=3⋅2√3g=6√3g
The total separation S between the two particles when their velocities are perpendicular:
S=d1+|d2|=8√3g+6√3g=14√3g
Assuming g≈10m/s2:
S=14√310≈2.42m
Similar Questions
Two balls A and B are projected from the same position with horizontal velocity 20ms−1 and 5ms−1 as shown. The separation between these two bodies at the moment their velocities become perpendicular to each other is x m. The value of x is
View SolutionFrom the top of the tower, two balls are thrown horizontally in opposite directions with velocities u1 and u2. Find the distacne between the balls at the moment when their velocity vectors becomes mutually perpendicular. (Assume the height of tower very large)
View Solution
Knowledge Check
From a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The horizontal distance between two bodies, when their velocity are perpendicular to each other, is.A1 mB0.5 mC2 mD4 mTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
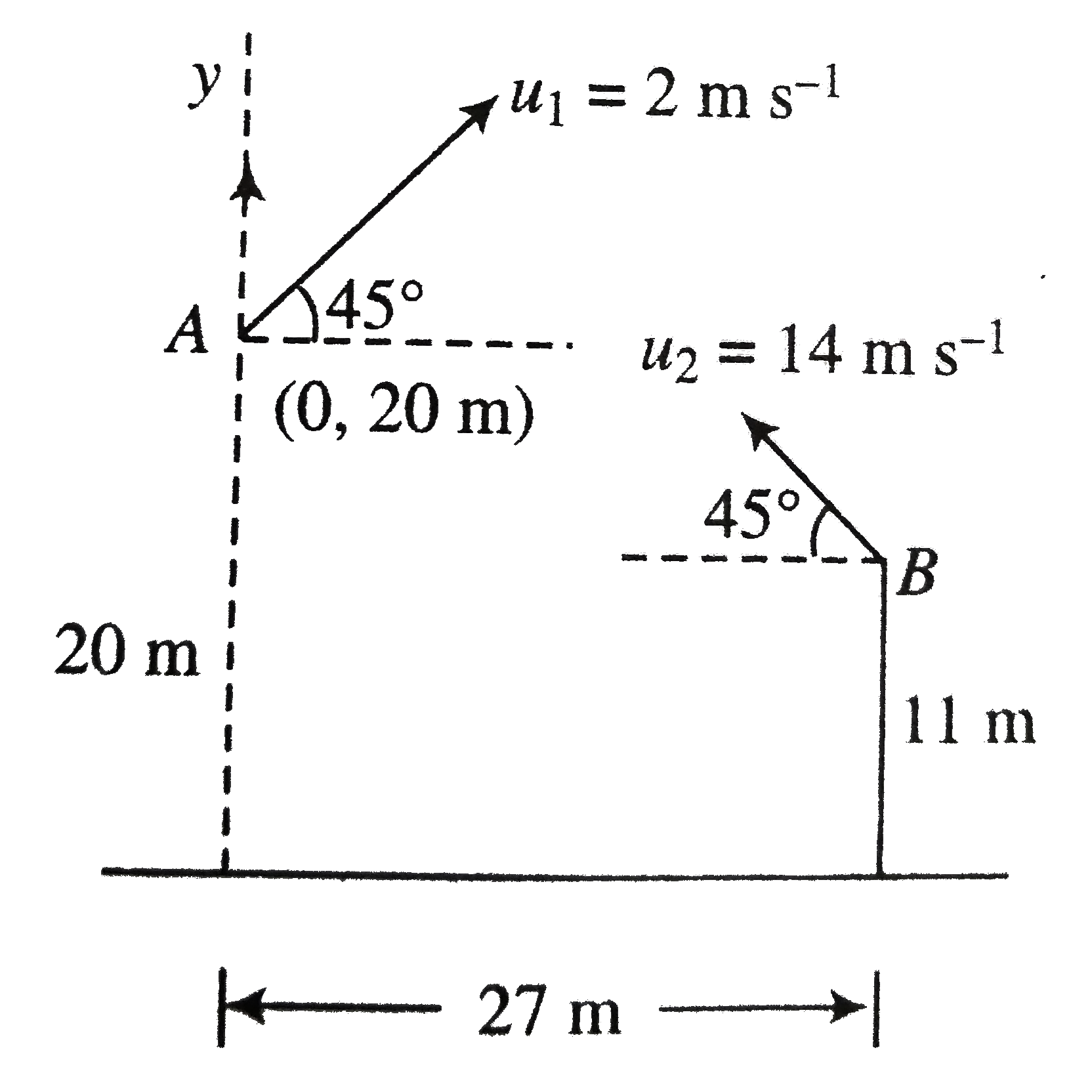
Minimum separation between A and B isA3 mB6 mC12 mD9 mFrom a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The time taken for the velocity vectors of two bodies to become perpendicular to each other is :A0.1 sB0.2 sC0.4 sD0.8 s
Two particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionTwo projectiles are projected horizontally from the same point in opposite directions with speed 5m/s . Find the separation in meter at the instant their velocities become mutually perpendicular (g=10m/s2).
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
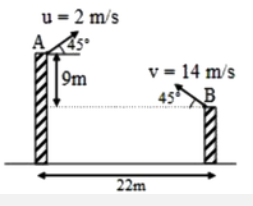
View SolutionFrom a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The time taken for the displacement vectors of two bodies to be come perpendicular to each other is.
View SolutionThe velocity of image object and mirror both are moving towards each other with velocities 4ms−1and5ms−1 respectively, is
View Solution

