Figure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., x←10 and x>15, U=0.
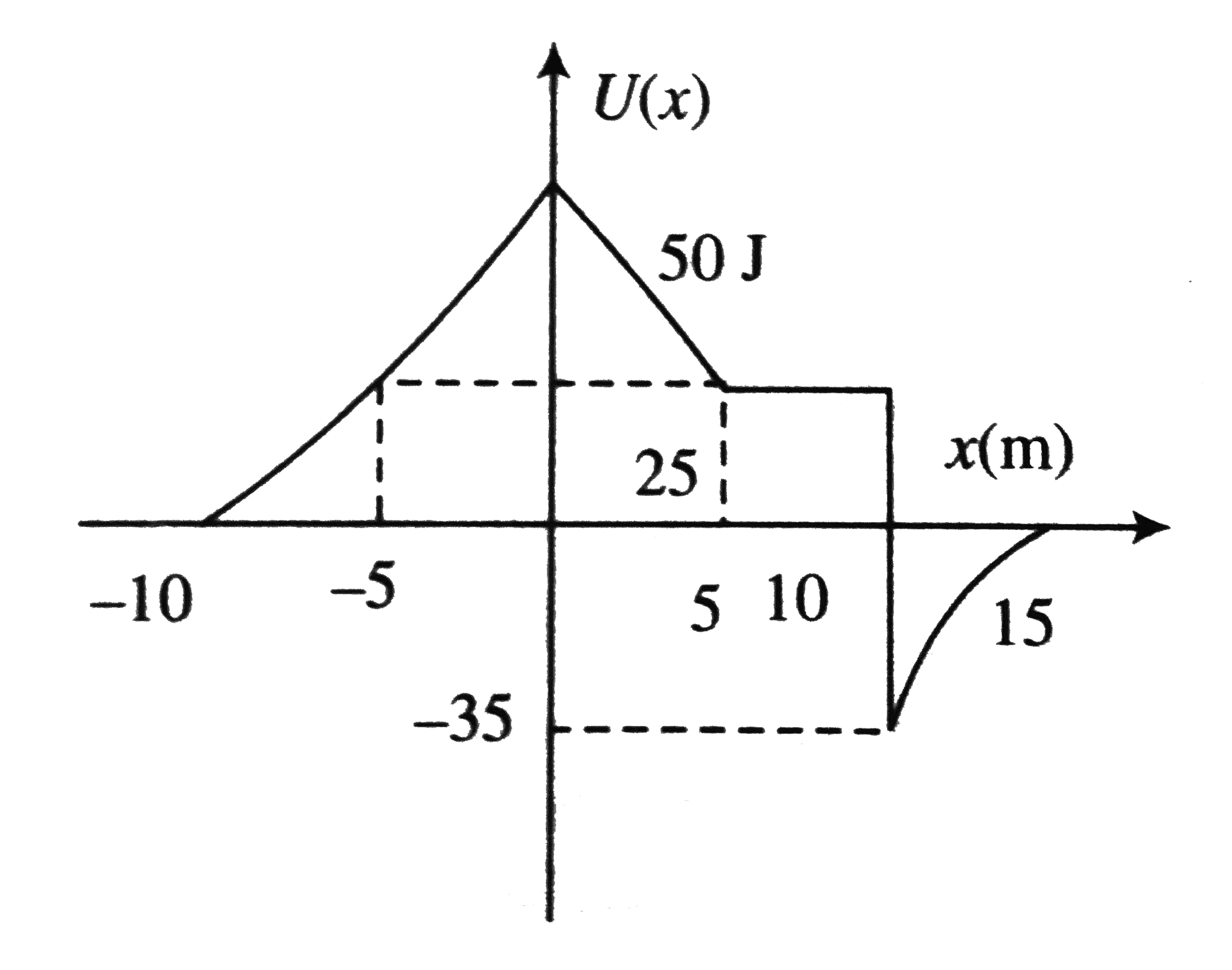
If the particle is isolated and its total mechanical energy is 60J, then
(a) The particle can be found anywhere from −∞<x<∞.
(b) The particle's maximum kinetic energy is 95J.
(c) The particle's kinetic energy is not getting zero
(d) All of the above
The correct Answer is:D
Here E=60J and as the system is isolated, the total mechanical energy remains conserved. It is clear from the give variation that U varies from −35J to 50J. So, K=E−U will be from 10J to 95J.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )
19 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Knowledge Check
Figure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., x←10 and x>15, U=0.
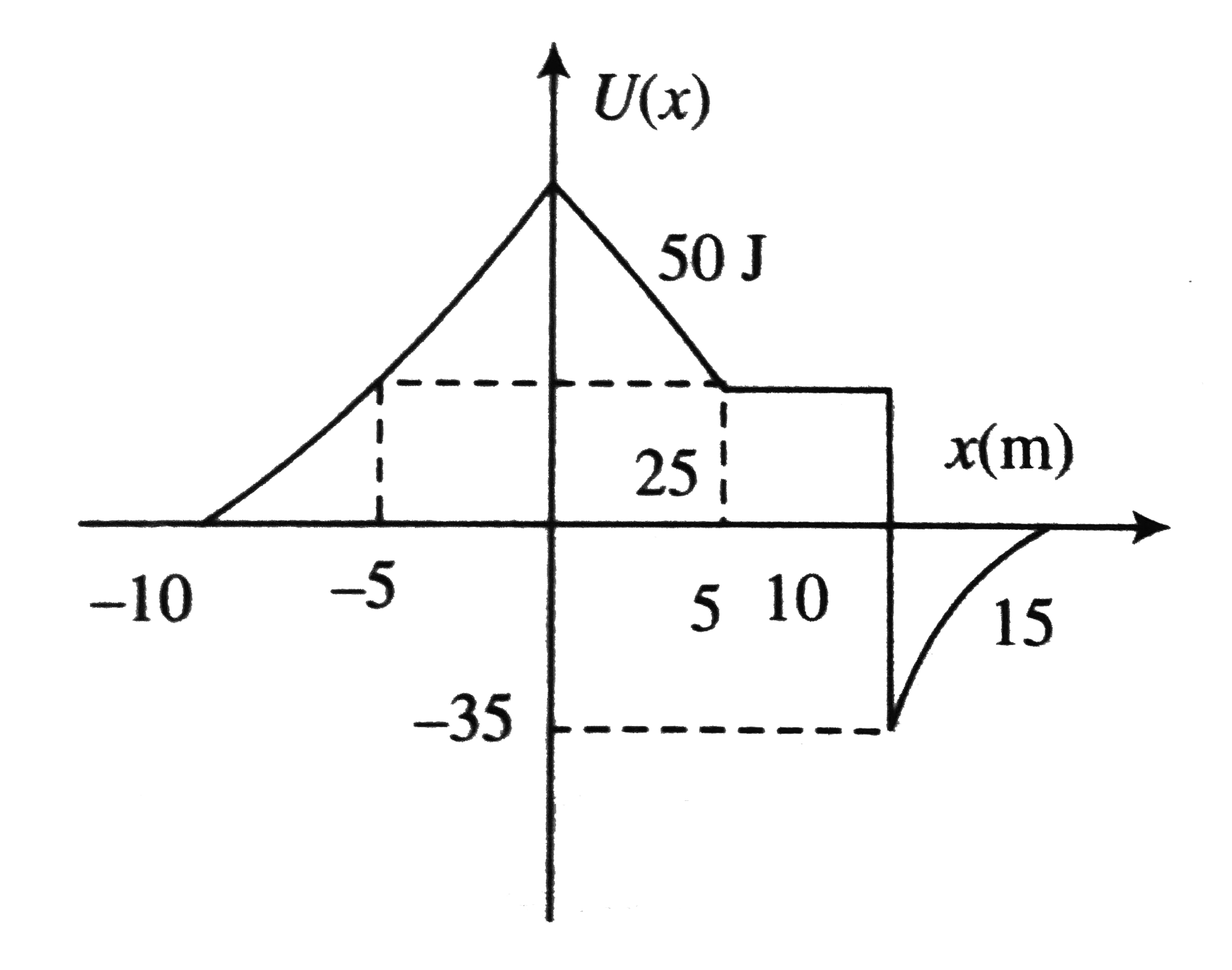
If the total mechanical energy of the particle is −40J, then it can be found in regionA(a) x←10 and x>15B(b) −10<x←5 and 6<x<15C(c) 10<x<15D(d) It is not possibleThe figure shows the variation of potential energy of a particle as a funcation pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
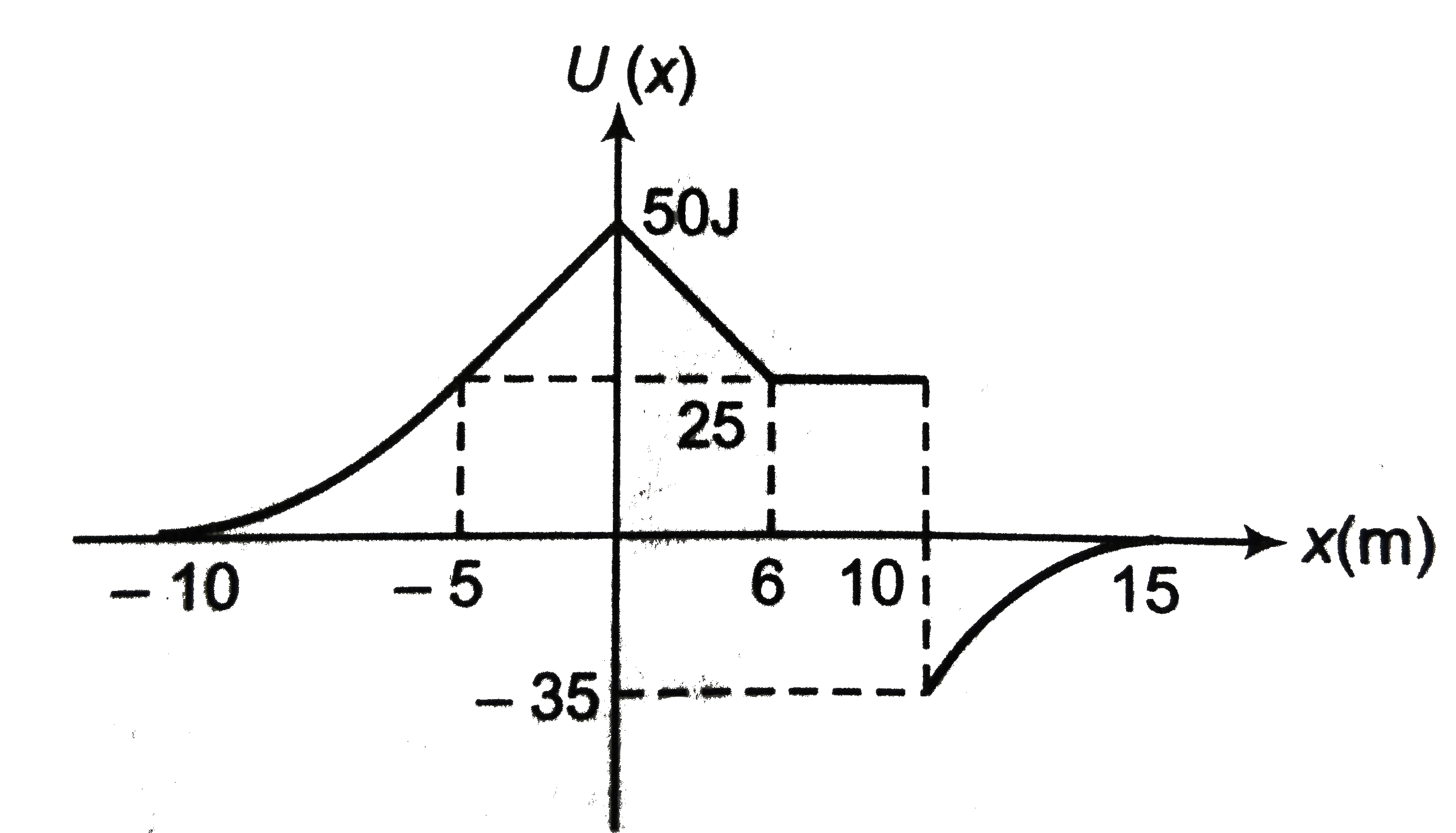
If total mechanical energy of the particle is −40J, then it can be found in region.Ax<10 and x>15B−10<x<5 and 6<x<15C10<x<15DIt is not possibleThe figure shows the variation of potential energy of a particle as a funcation pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
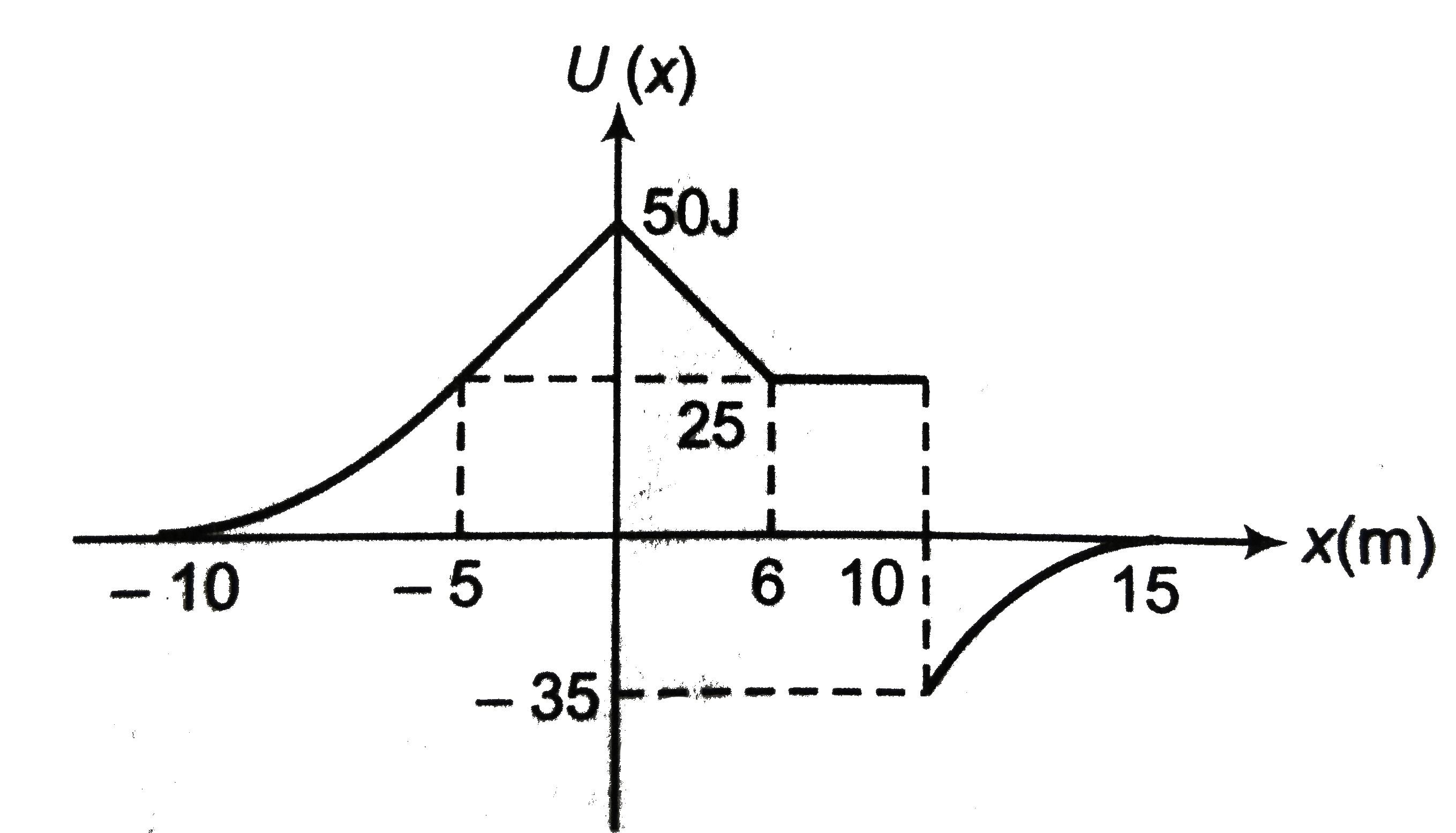
If total mechanical energy of the particle is 25J, then it can found in the regionA−10<x<−5 and 6<x<15B−10<x<0 and 6<x<10C−5<x<6D−10<x<10
Potential energy of a particle is related to x coordinate by equation x2−2x . Particle will be in stable equilibrium at :
View SolutionIn the fig. The potential energy U of a particle plotted against its position x from origin. Which of the following statement is correct
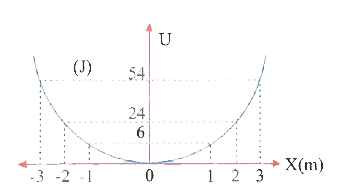
View SolutionFigure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
View SolutionThe potential energy of a particle is given by formula U=100−5x+100x2,whereU and are .
View SolutionIf x,F and U denote the dispalcement, force acting on and potential energy of a particle then
View Solution