The figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on . For all other values is zero. i.e. for and .
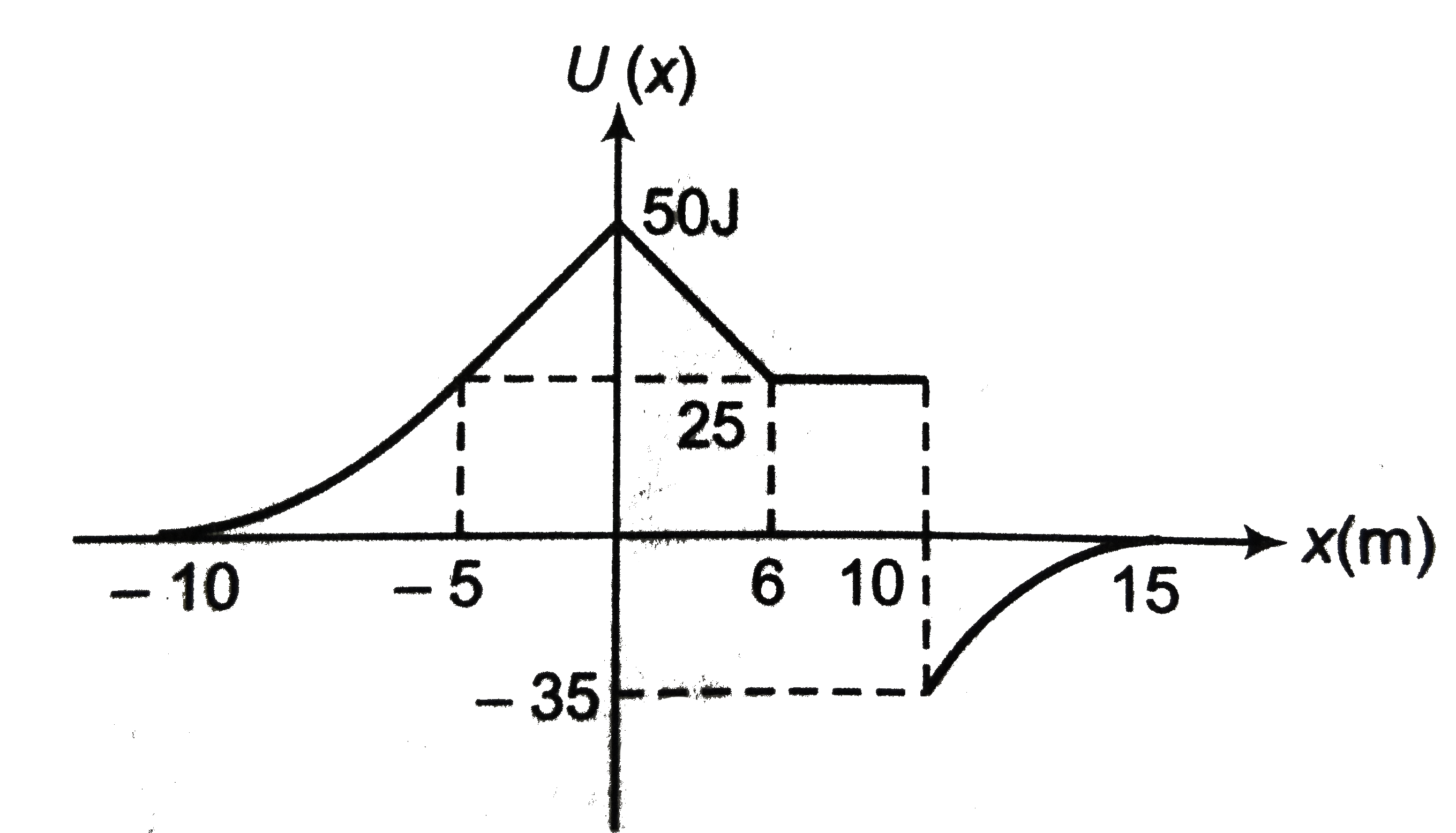
If total mechanical energy of the particle is , then it can found in the region
(a) and
(b) and
(c)
(d)
The correct Answer is:A
The concept used in solving these questions is that kinetic energy can never be negative. It would always be non-negative.
Total mechanical energy
Here if , then
For K to be non-negative, , which is the case for and .
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )
19 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Knowledge Check
The figure shows the variation of potential energy of a particle as a funcation pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
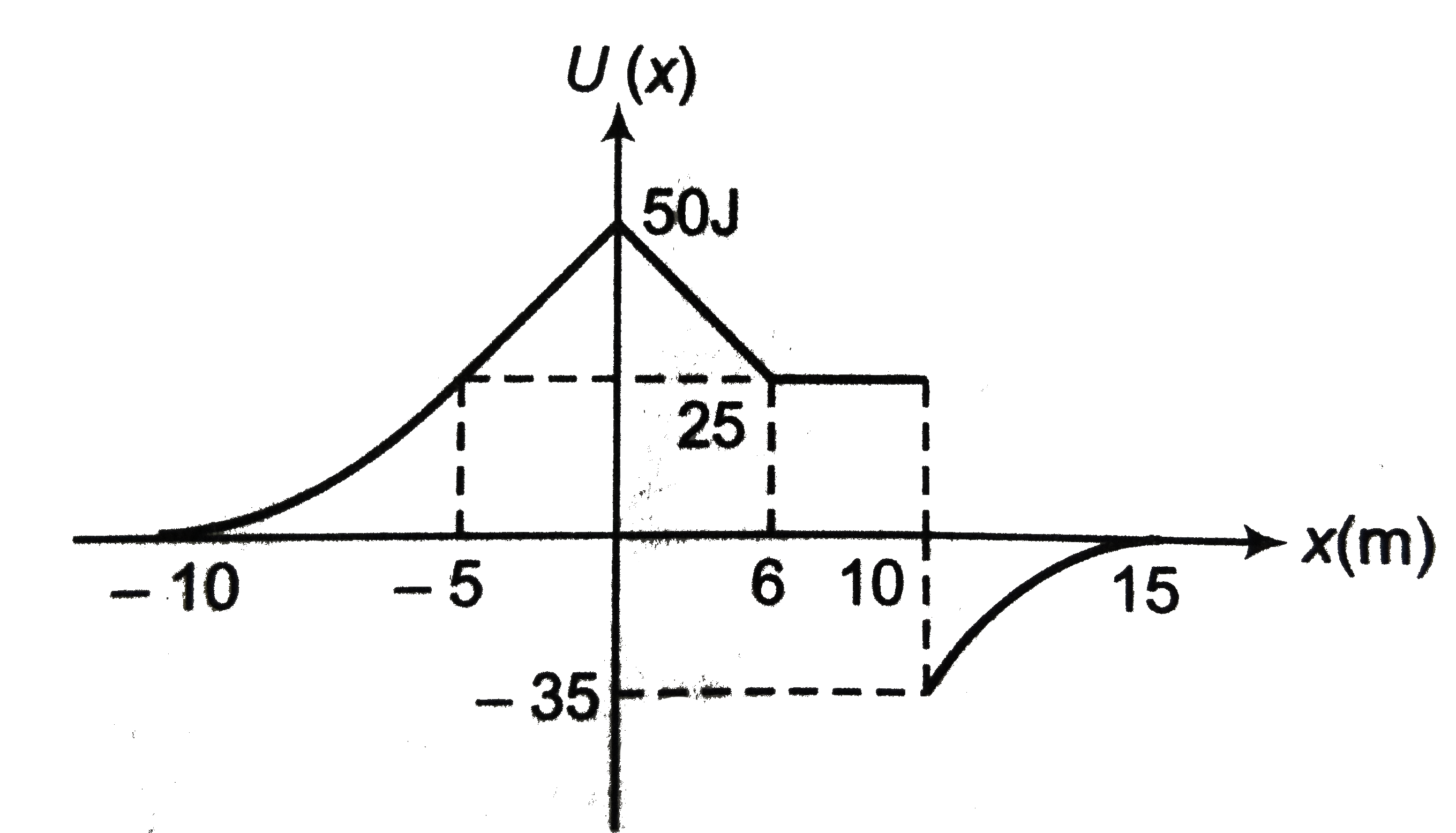
If total mechanical energy of the particle is −40J, then it can be found in region.Ax<10 and x>15B−10<x<5 and 6<x<15C10<x<15DIt is not possibleFigure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., x←10 and x>15, U=0.
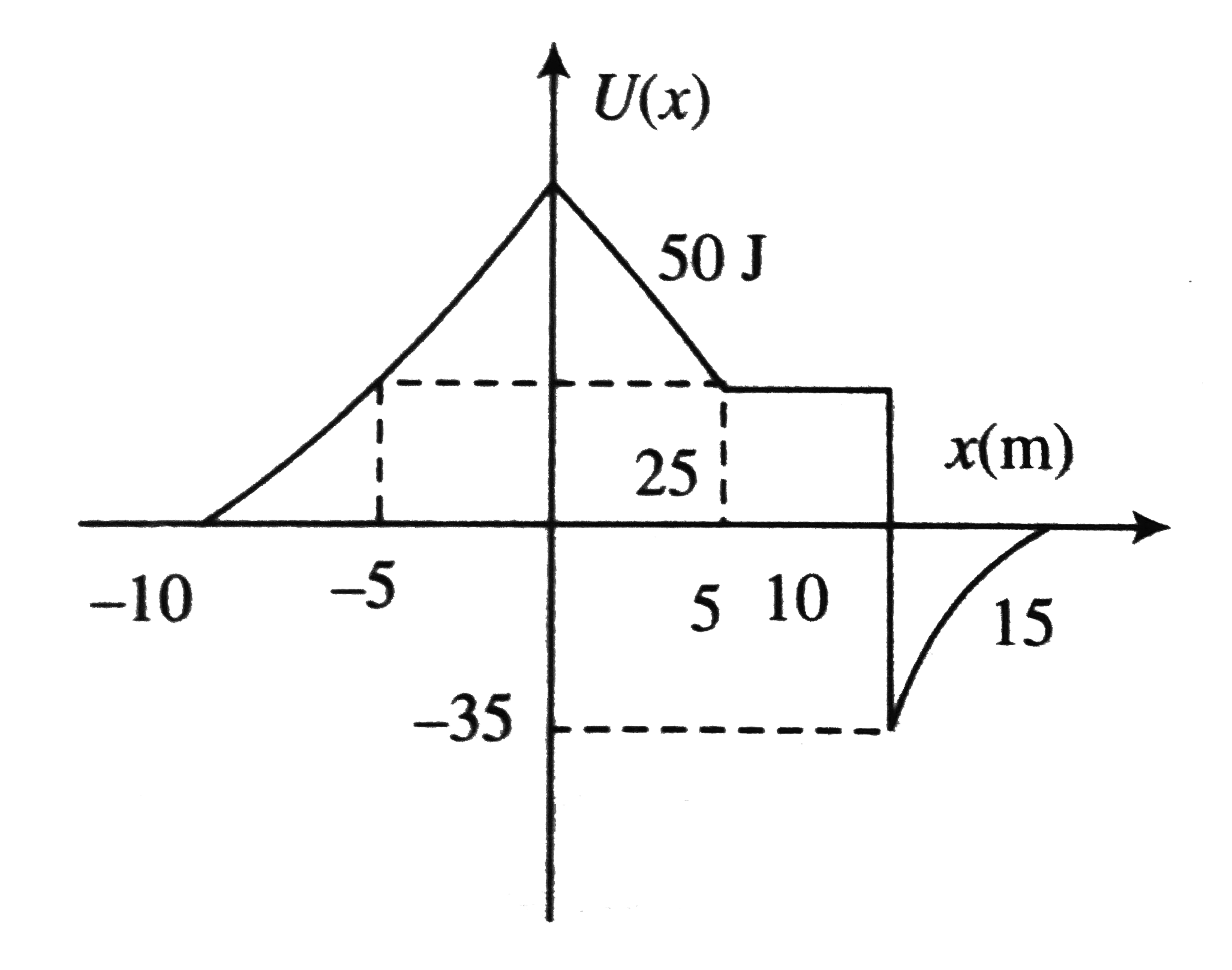
If the total mechanical energy of the particle is −40J, then it can be found in regionA(a) x←10 and x>15B(b) −10<x←5 and 6<x<15C(c) 10<x<15D(d) It is not possibleFigure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., x←10 and x>15, U=0.

If the particle is isolated and its total mechanical energy is 60J, thenA(a) The particle can be found anywhere from −∞<x<∞.B(b) The particle's maximum kinetic energy is 95J.C(c) The particle's kinetic energy is not getting zeroD(d) All of the above
The potential energy of a particle of mass m is given by U=12kx2 for x<0 and U=0 for x≥0. If total mechanical energy of the particle is E. Then its speed at x=√2Ek is
View SolutionThe following plot shows the variation of potential energy (U) of a system versus position (x). From the graph we can interpret that :
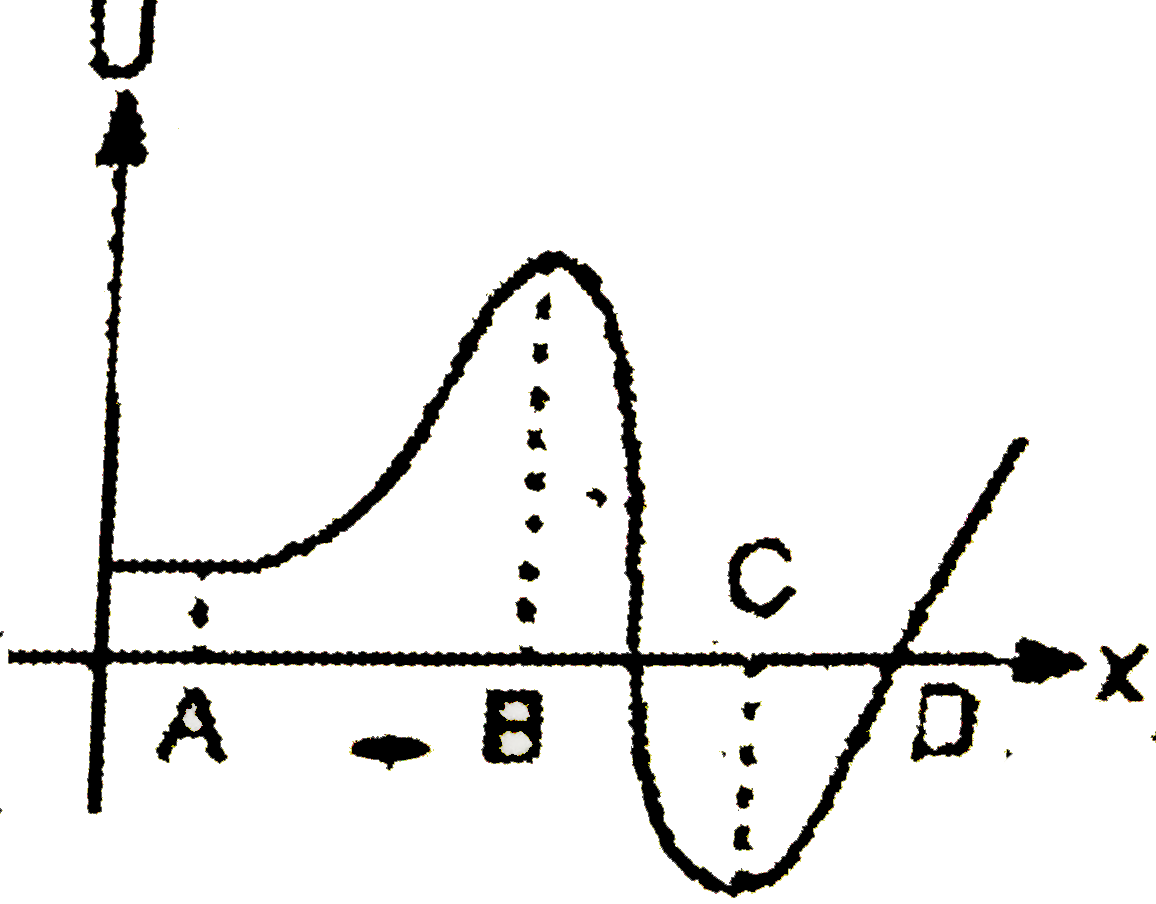
View SolutionPotential energy curve U of a particle as function of the position of a particle is shown. The particle has total mechanical energy E of 3.0 joules. Then select correct alternative.
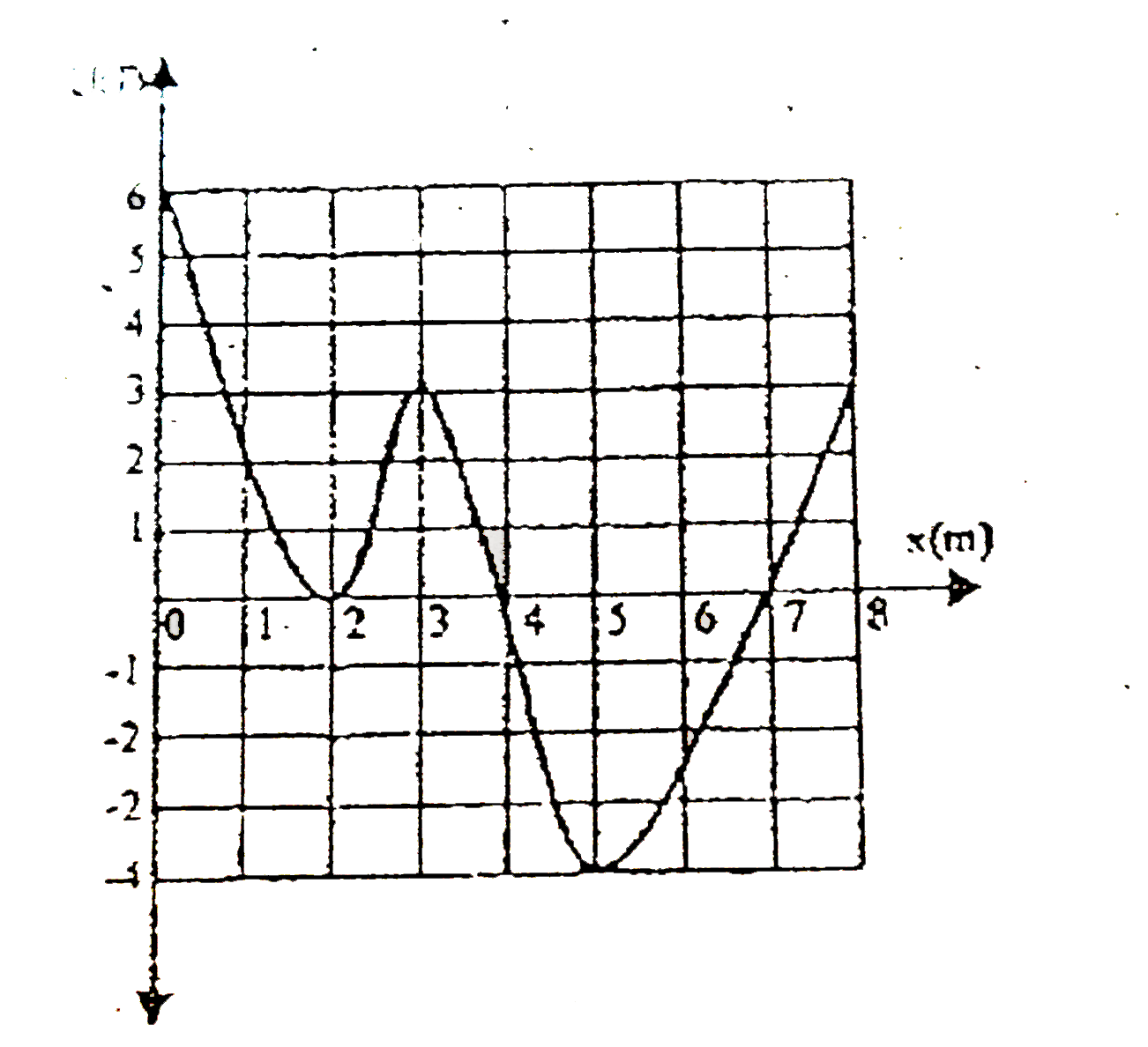
View SolutionThe potential energy of a particle varies with x according to the reltiaon U(x) =x2−4x. The point x =2 is a point of
View SolutionThe potential energy of a particle of mass m is given by U=12kx2 for x<0 and U=0 for x≥0. If total mechanical energy of the particle is E. Then its speed at x=√2Ek is
View Solution
