In the situation shown in figure all contact surfaces are smooth. The force constant of the spring is K. Two forces F are applied as shown. The maximum elongation produced in the spring is how many times of F/K (initially the spring is relaxed)?
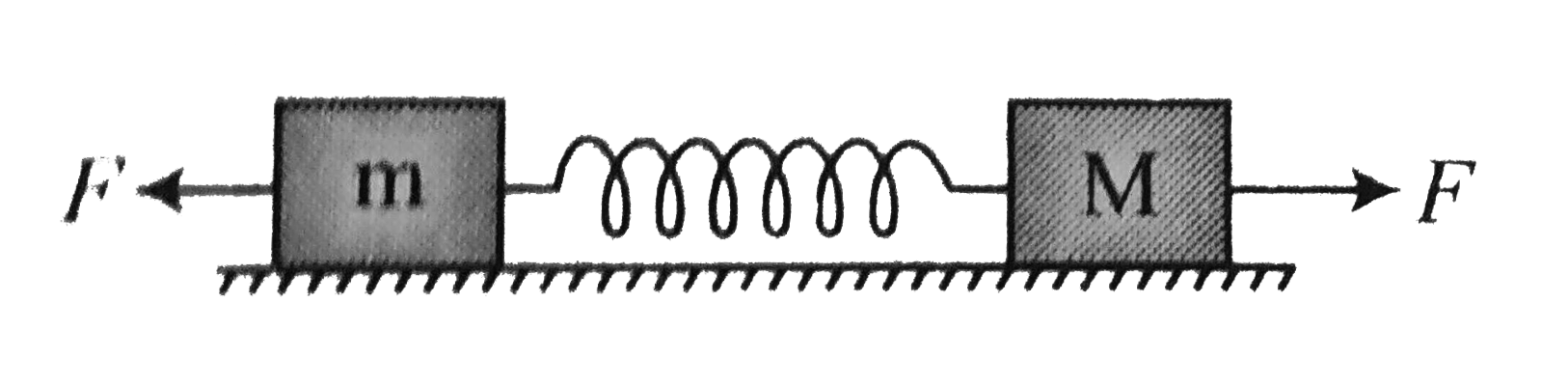
The correct Answer is:(2)
Maximum elongation is given by
xmax=2[F1m2+F2m1]K(m1+m2)
Here F1=F2=F, m1=m and m2=M
Put the values and solve to get xmax=2F/K
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Archives (sinble Correct )
Explore 19 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Archives(multiple Correct)
Explore 3 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
In the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.

View SolutionIn the diagram shown, no friction at any contact surface. Initially, the spring has no deformation. What will be the maximum deformation in the spring ? Consider all the strings to be sufficiency large. Consider the spring constant to be K.
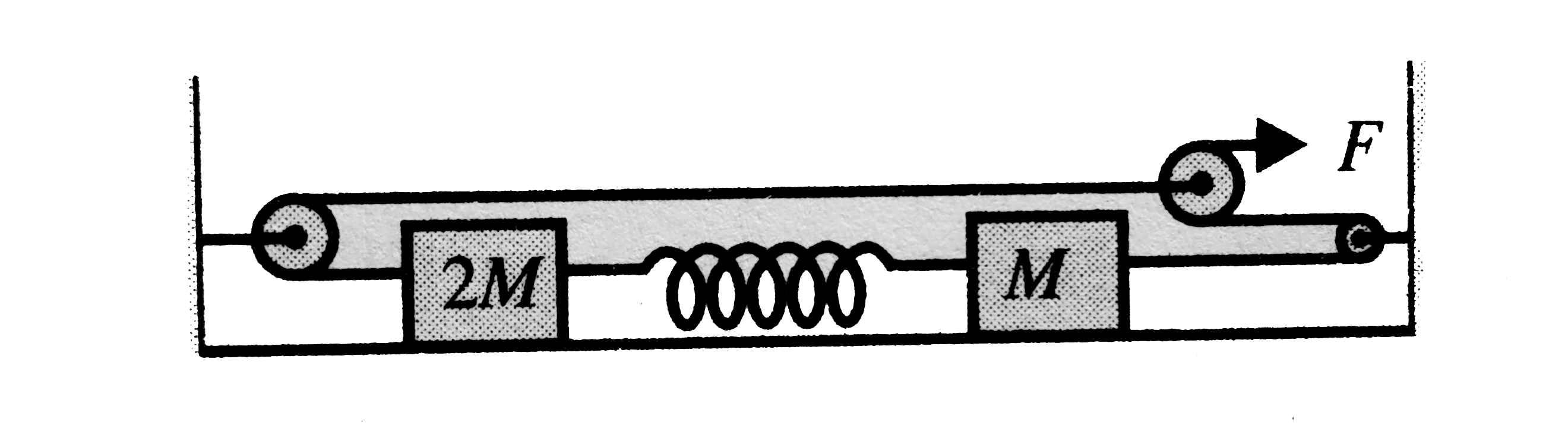
View Solution
Knowledge Check
Force constant of a spring (k) is anonymous to
AYALBYLACALYDALYWhat will be the force constant of the spring system shown in figure?
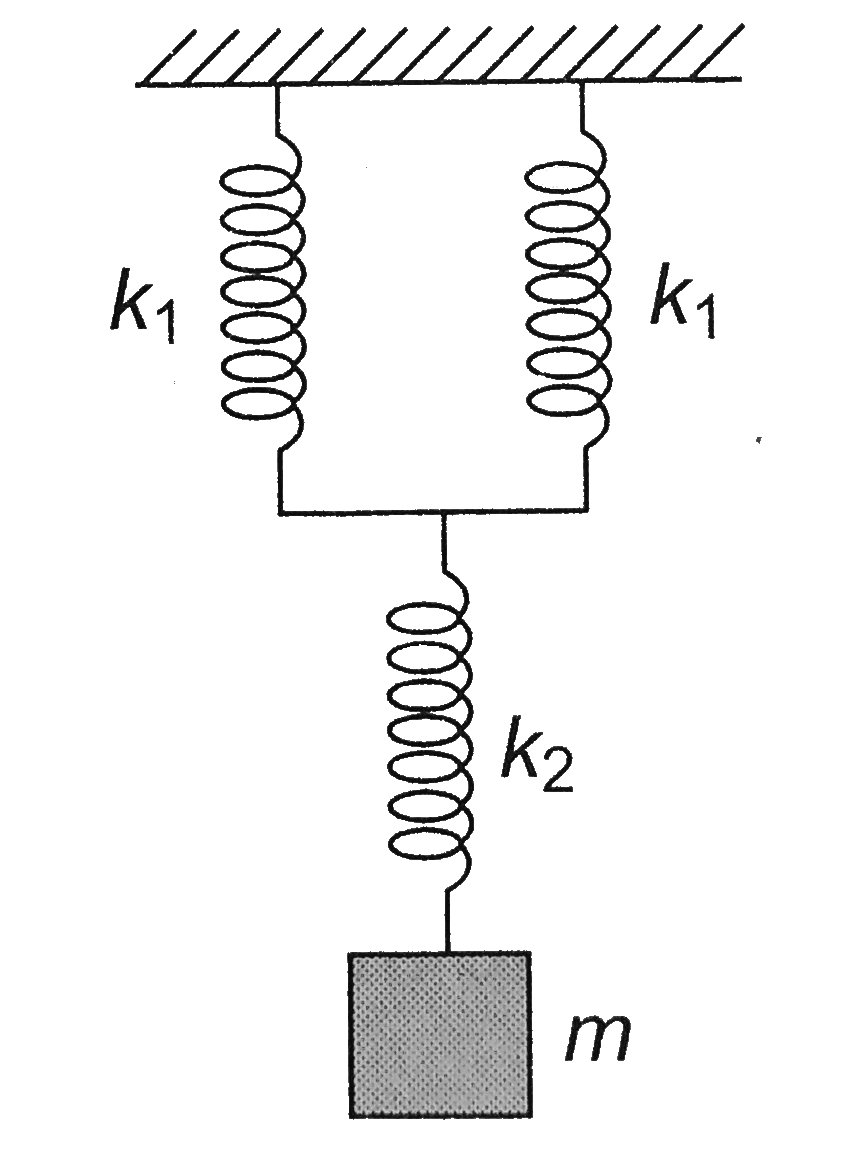 A[1k1+1k2]B[12k1+1k2]−1C[1k1+1k2]−1D[12k1+1k2]
A[1k1+1k2]B[12k1+1k2]−1C[1k1+1k2]−1D[12k1+1k2]Two springs have their force constants in the ratio of 3:4. Both the springs are stretched by applying equal force F. If elongation in first spring is x then elogation is second spring is
A3xB4xC43xD34x
In the diagram shown, no friction at any contact surface. Initailly, the spring has no deformation .What will be the maximum deformation in the spring? Consider all the strings to be sufficiently large. Consider the spring constant to be K.
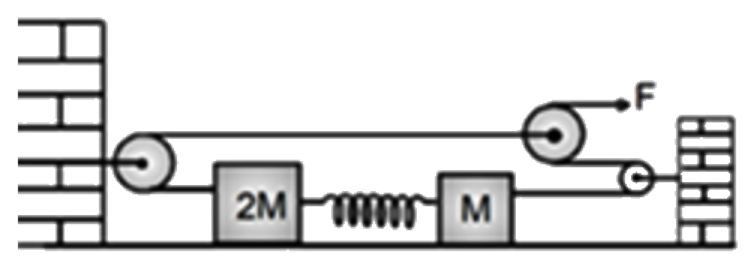
View SolutionIn the diagram shown, no friction at any contact surface. Initially, the spring has no deformation what will be the maximum deformation in the spring? Consider all the strings to be sufficiency large. Consider the spring constant to be K.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
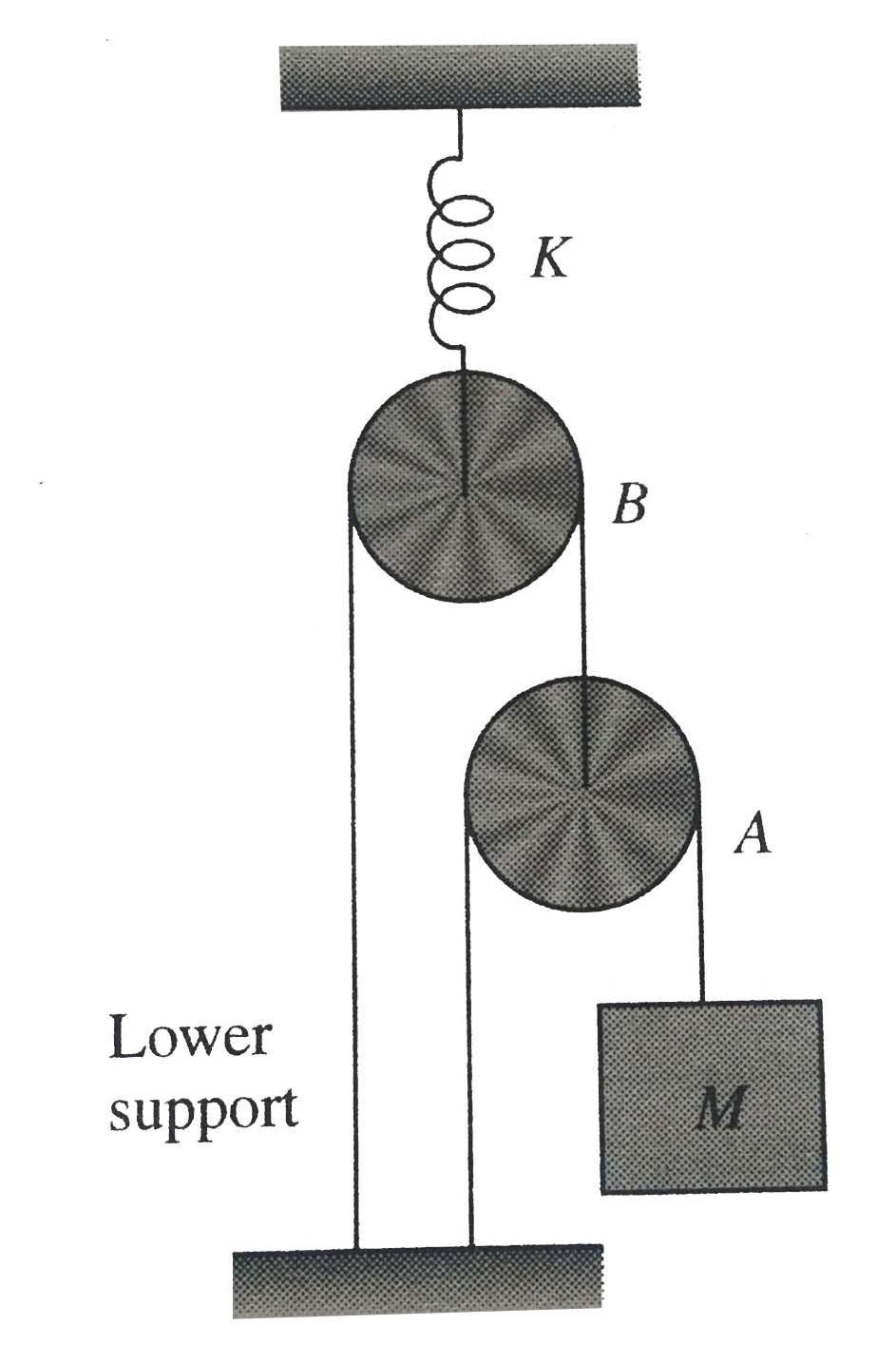
The extension produced in the spring is given by
View SolutionThe effective spring constant of two spring system as shown in figure will be

View Solution

