A small wedge whose base is horizontal is fixed to a vertical rod as shown in fig . The sloping side of the weidgeis frictionless and the wedge is span with a constant angular speed ω about vertical axis as shown in the fig find the
a. value of angular speed ω for which the block of mass m just does not slide down the wedge.
b. normal reaction on the block by wedge when block does not slip relative to wedge.

The free body diagram of the block is
a. For block not to slide wedge appling Newton's second law along incline we get
mgsinθ=mω2(lcosθ)cosθ
ω=√gsinθ1cosθ
b. Appling Newton 's second law along normal to the wedge

we get N=mgcosθ+mω2(1cosθ)sinθ
=mgcosθ+mgsinθ1cos2θ1cosθsinθ=mgsecθ
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Subjective
Explore 21 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Single Correct
Explore 87 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Exercise 7.2
Explore 16 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A vertical U-tube is spinned about the vertical axis passing through the left hand limb, with an angular speed ω such that the liquid columns in the limbs have heights h and 3h, as shown in the figure. Find the value of to ω.
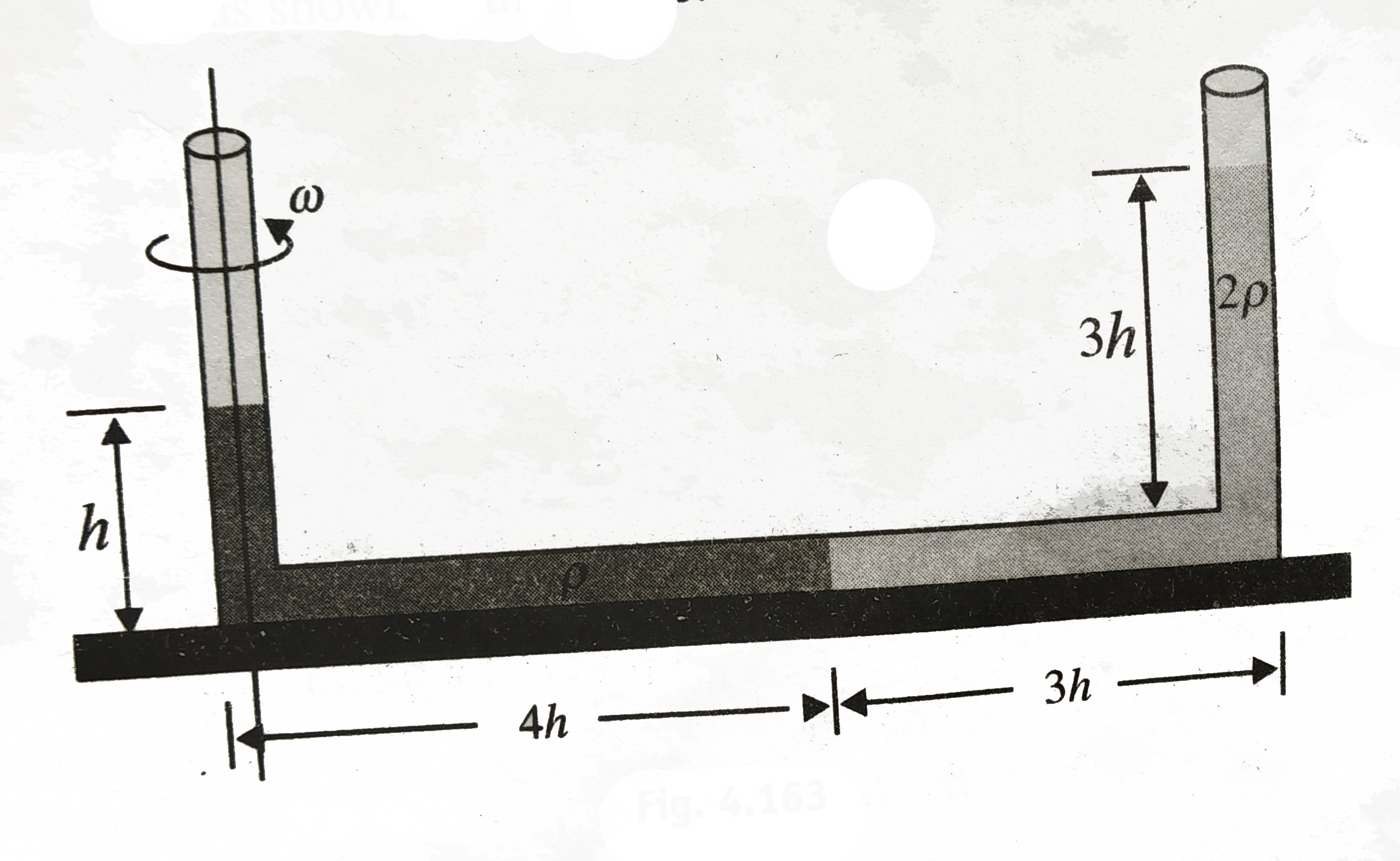
View SolutionFind total energy of the inclined rod of mass m shown in figure-5.39 , rotating with angular velocity ω , about a vertical axis XX', shown in figure .

View Solution
Knowledge Check
Block of mass m is stationary w.r.t. wedge. Normal force exerted by wedge on the block is
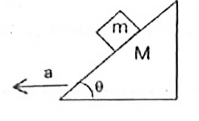 AmgcosθBmgcosθCmgsinθDmgsinθ
AmgcosθBmgcosθCmgsinθDmgsinθA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
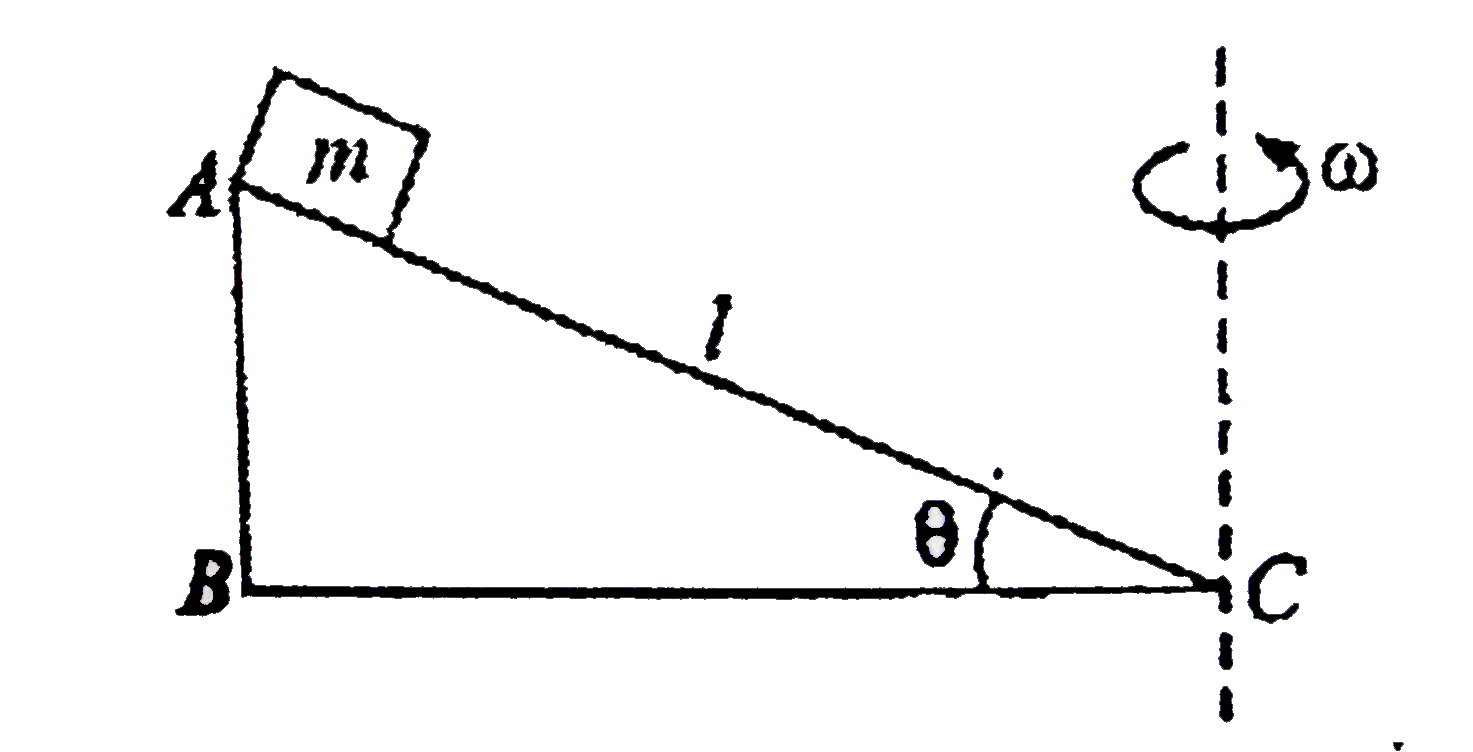 A⎛⎝√gsinθl⎞⎠secθB(√gl)cosθC(√glcosθ)cosθD√gsinθl
A⎛⎝√gsinθl⎞⎠secθB(√gl)cosθC(√glcosθ)cosθD√gsinθlThe minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
Ag(cosθ+μsinθsinθ−μcosθ)Bg(sinθ+μcosθcosθ−μsinθ)Cg(sinθ−μcosθsinθ+μcosθ)Dg(cosθ−μsinθsinθ+μcosθ)
In the arrangement shown in the fig. the block of mass m lies on the wedge. Wedge is moving with acceleration a = 5 m/sec . Find the wedge acceleration of the block with respect to wedge.
View SolutionIn the arrangement shown in the fig. the block of mass m lies on the wedge. Wedge is moving with acceleration a = 5 m/sec Find the wedge acceleration of the block with respect to wedge.
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionL shaped rod whose one end is horizontal and other is vertical is rotating about a vertical axis as shown with angular speed ω .The sleeve has mass m and friction coefficient between rod and sleeve is μ.The minimum angular speed ω for which sleeve cannot slip on rod is?
View SolutionA block of mass m is placed on a smooth wedge of wedge angle θ The whole system is accelerated horizontally so that the block does not slip on the wedge. The force (normal reaction) exerted by the wedge on the block has a magnitude:
View Solution

