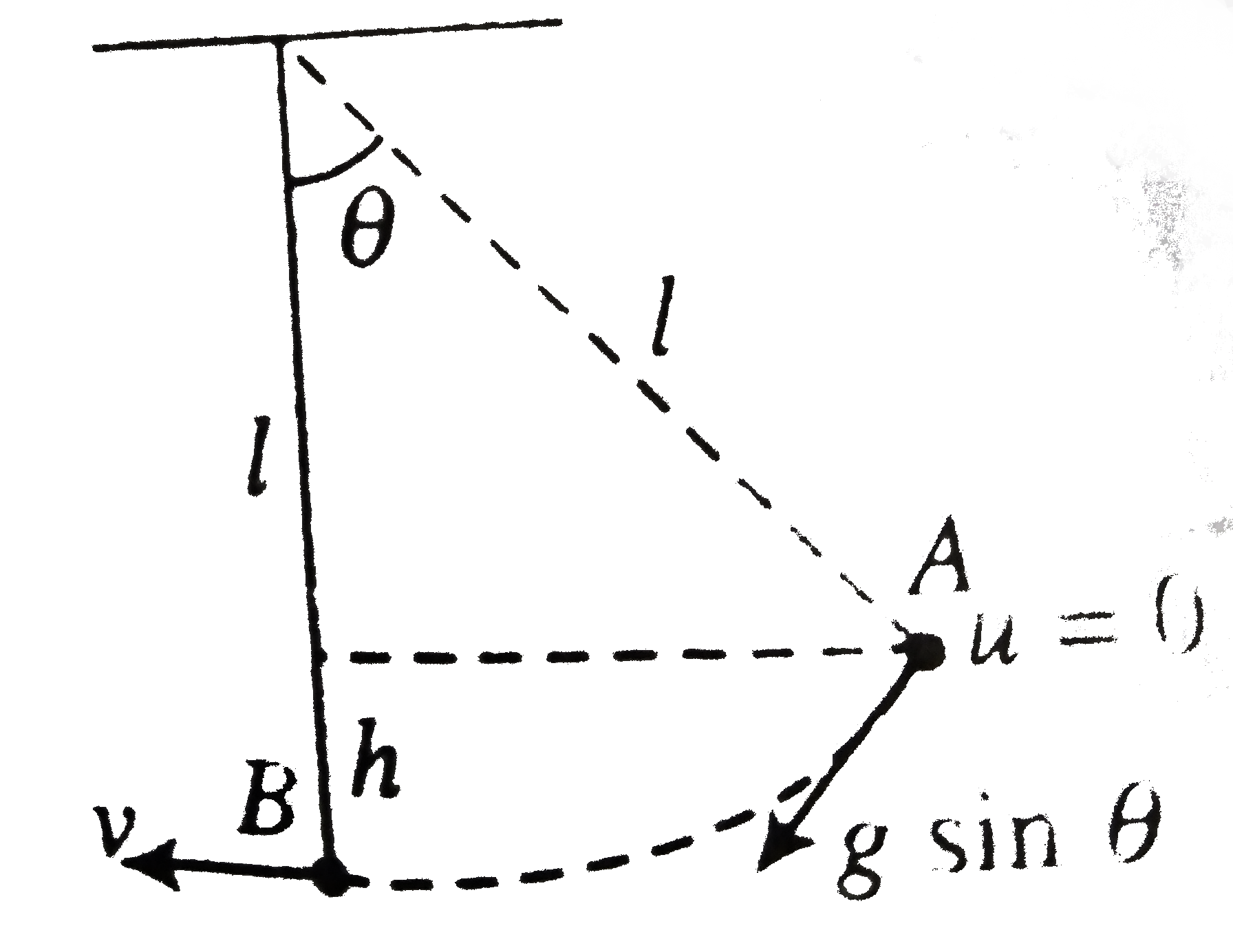
A ball suspended by a thread swings ia a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle θ of thread deflection in the extreme position will be
Acceleration at point A,a1=gsinθ at point B,a2=v2l
where v=√2gh=√2g(1−1cosθ)
⇒a2=2g(1−cosθ)
Givena1=a2⇒gsinθ=2g(1−cosθ)
Squaring both sides and solving we get
cosθ=35⇒θ=53∘
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
(a) A ball, suspended by a thread, swings in a vertical plane so that the magnitudes of its acceleration in the extreme and the lowest positions are equal. Find the maximum deflection of the thread with respect to the vertical.
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the magnitude of the force acting on the particle as a function of s.
View SolutionA small bob suspended by a thread swings in a vertical plane so that angle made by thread in extreme positions with the vertical is θ=sin−1(45) What is the ratio of acceleration of bob in extreme position to its acceleration in lowest position?
View Solution
Knowledge Check
A ball suspended by a thread swings in a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle of thread deflection in the extreme position will be - 2
Atan−1(2)Btan−1(√2)Ctan−1(12)D2tan−1(12)Particle moves from extreme position to mean position, its
Akinetic energy increases, potential energy decreasesBkinetic energy decreases, potential increasesCboth remains constantDpotential energy becomes zero and kinetic energy remains contantA ball attached to one end of a stringj swings in a vertical plane such that its acceleration at point A (exterme posiuion) is eqal to its acceleration at point B (mean posirion), The angle θ is
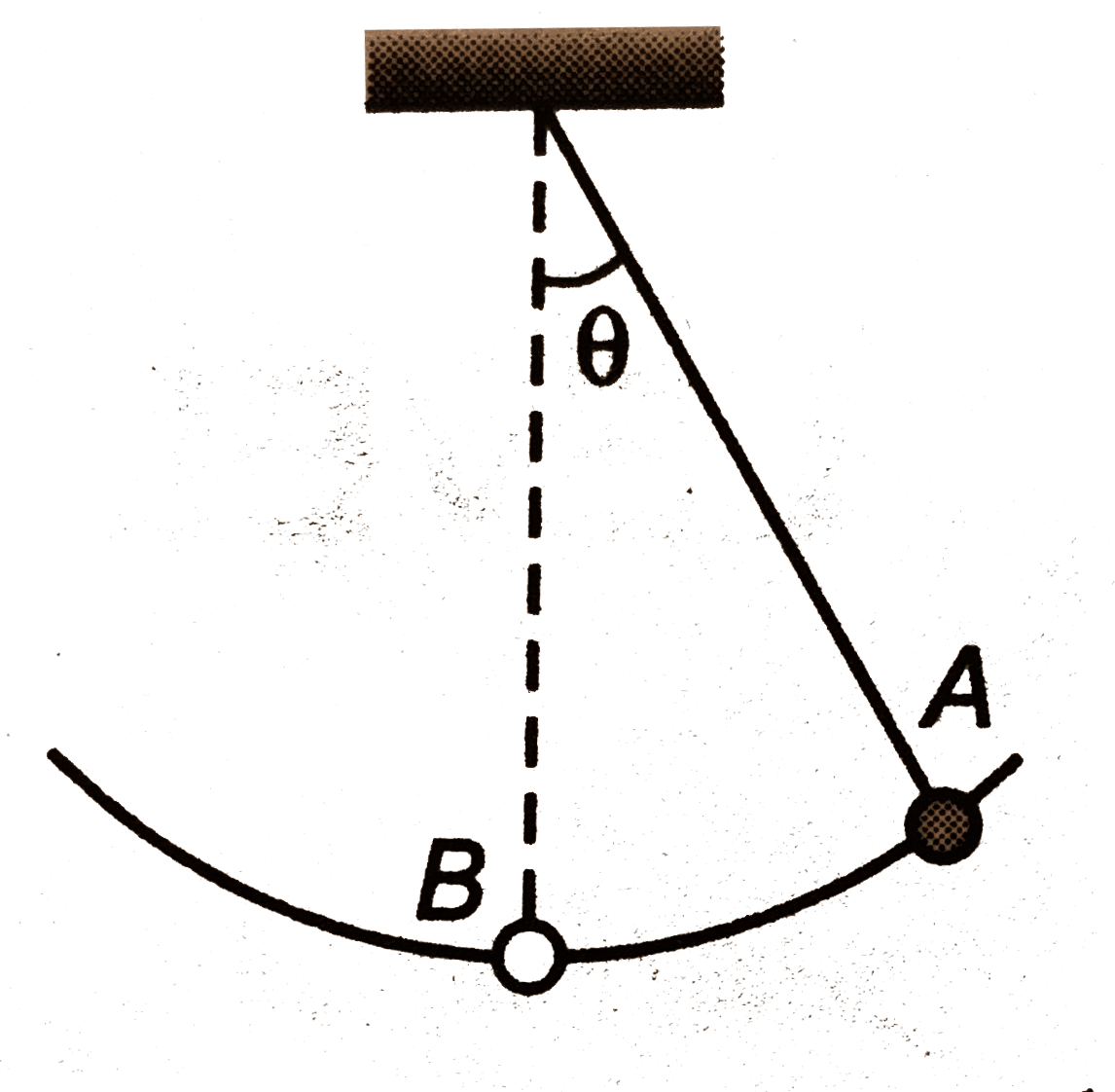 Acos−1(25)Bcos−1(45)Ccos−1(35)DNone of these
Acos−1(25)Bcos−1(45)Ccos−1(35)DNone of these
A rod of mass m and length l suspended from a point swings in a vertica plane such that magnitude of acceleration of its C.M. at extreme points is same as that at the mean point then :
View SolutionThe velocity at mean position and acceleration at the extreme position have the phase difference of
View SolutionThe acceleration of a particle performing S.H.M. at extreme position is
View SolutionA short boy sits on a seat suspended by a light string from a fixed point O and starts swinging in a vertical plane from the extreme position P with a small amplitude the graph which shows the variation of the tension in the string with time 't' is:
View SolutionA small sphere of mass m suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
View Solution
