An old record player of 15.0cm radius at 33.0rev1min while mounted on a 30∘ incline as shown in figure
a. If a mass m can be placed anywhere on the rotaing record , where is the most critical place on the disc where slipping might occur ?
b.Calculate the least possible coefficient of friction that must exist if no slipping occurs.
a. Rim
b. Maximum friction is required at bottom most point as μ calculate here will be the least value repaired
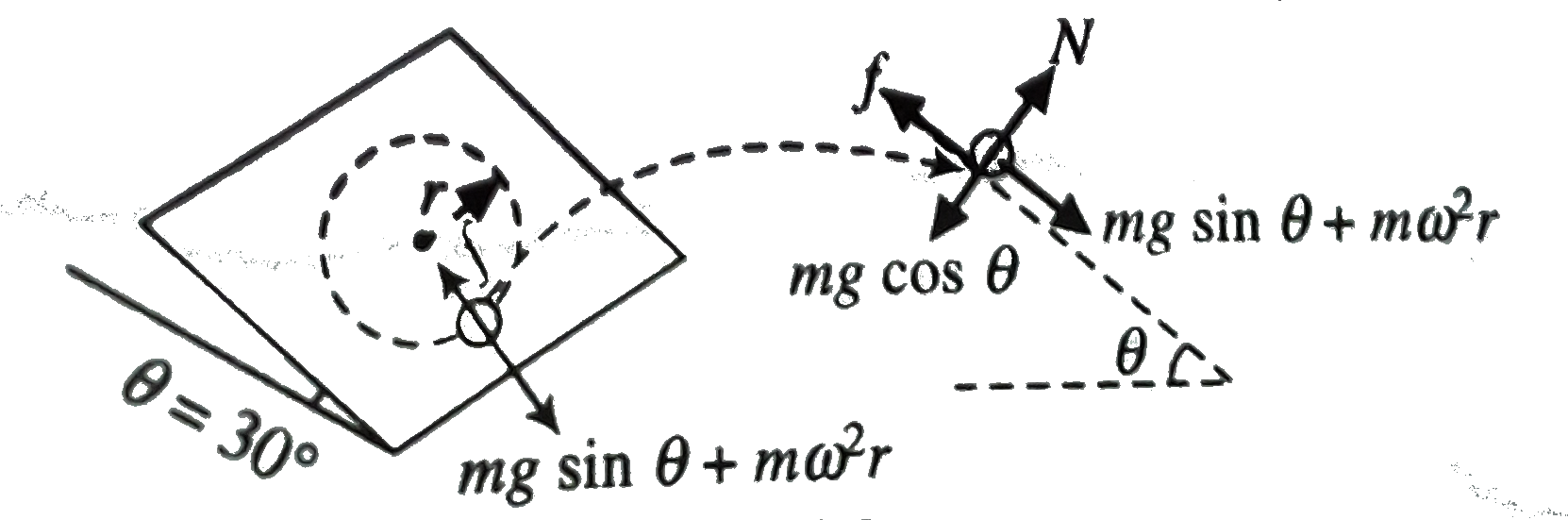
f≥mgsinθ+mω2r
μmgcosθ≥mgsinθ+mω2r
μ≥tanθ+ω2rgcosθ=1√3+4π2×1089×303600×1000×√3
=1√3+4π2×3634√3×1000
=1√3[(1+π2×36310.000)]
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
An old record player of 10mathrm(~cm) radius turns at 10rads while mounted on a 37∘ incline as shown in the figure. A particle of mass m can be placed anywhere on the rotating record. If the least possible coefficient of friction that must exist for no slipping to oceur is μ, then find 4μ.
'(##CEN_KSR_PHY_JEE_C07_039_Q24##)A block is.moving in horizontal circular motion with constant speed of 10ms (with respect to lift) about a point O on the smooth surface of the lift. The lift is moving upward with constant speed of 10ms and the length of string of the lift is 2m, The radius of curvature (in m ) of the motion of block with respect to ground is
'(##CEN_KSR_PHY_JEE_C07_038_Q23##)'
View SolutionA block of mass 1kg is placed on the periphery of a rotating rough circular table of radius 50cm as shown in the figure.Angular velocity of the table is 4 rad/s.The minimum value of coefficient of friction between the contact such that there is no relative slipping is (g=10ms2)
_PHY_E05_167_Q01.png)
View Solution
Knowledge Check
A boy is pulshing a ring of mass 3 kg and radius 0.6 m with a stick as shown in figure. The stick applies a force of 3N on the ring and rolls it without slipping with an acceleration of 0.4 m/s2
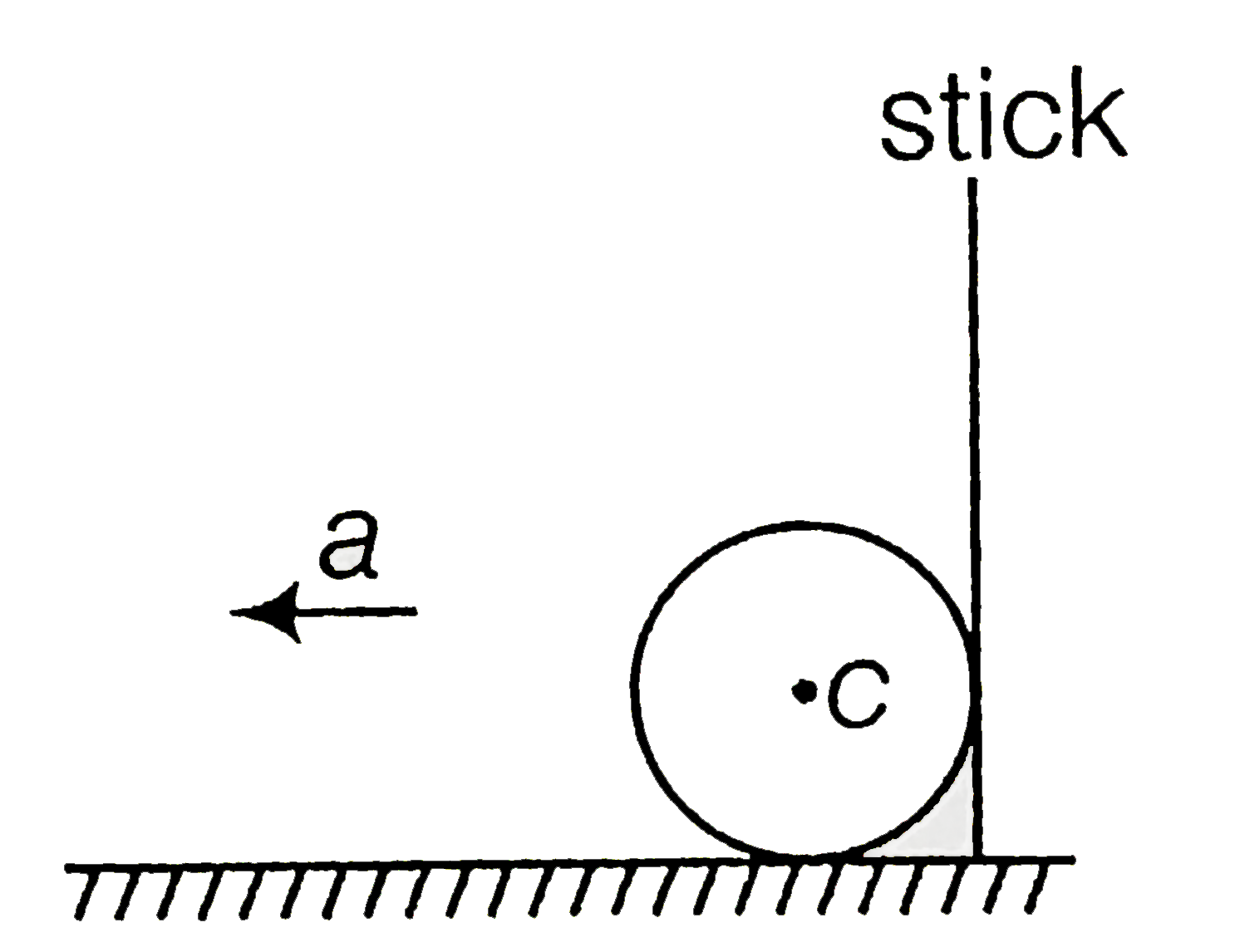The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficeient of friction between the stick and the ring is f10 The vlaue of F is A2NB4NC6ND3NA sufficiently long plane of mass 4kg is placed on a smooth horizontal surfaces A small block of mass 2kg is placed over the plank and is beging acted upon by a time verying horizontal force F=(0.5t) where F is in newton and t is in second as shown in figure. The coefficient of friction slipping the plank and the block is given is μs=μk=μ time t=12s the relative slipping between the plank and the block is just likely to accor
The coefficient of friction μ is equal toA0.10B0.15C0.20D0.30A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick applies a force of 2 N on the ring and rolls it without slipping with an acceleration of 0.3m/s2. The coeffecient of friction between the ground and the ring is large enough that rolling always occur and the coefficient of friction between the stick and the ring
A0.4B0.8C0.2D0.5
A boy is pushing a ring of mass 2kg and radius 0.5 m with a stick as shown in figure. The stick applies a force of 2N on the ring and rolls it without slipping with an acceleration of 0.3ms2. The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring of (P/10). The value of P is
View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.
View SolutionBlocks A and Bin the Fig. 2E.46 .(a) are connected With a string of negligible mass. The masses are placed on an inclined plane of inclination 30∘ as shown inFig. 2E.46 (a) . If A and B each have mass m and μA=0 and μR=√23, where μA and μB are the coefficient of friction between plane and the bodies respectively, calculate the acceleration of the system and tension in the string.
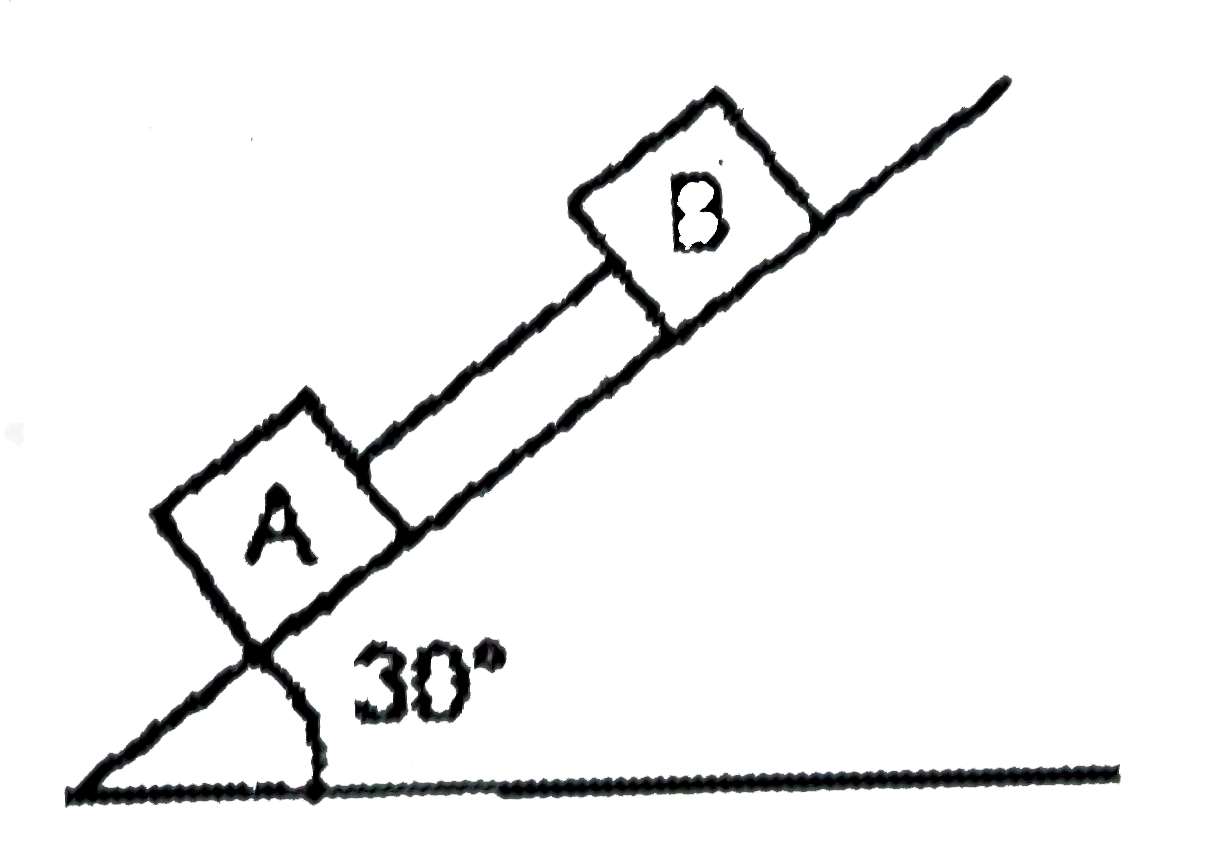
View SolutionA block of mass m height 2h and width 2b rests on a flat car which moves horizontally with constant acceleration a as shown in figure. Determine
a. the value of the acceleration at which slipping of the block on the car starts, if the coefficient of friction is μ.
b. the value of the acceleration at which block topples about A, assuming sufficient friction to prevet slipping and
c. the shortest distance in which it can be stopped from a speed of 20ms−1 with constant deceleration so that the block is not disturbed. The following data are given b=0.6m,h=0.9μ=0.5 and g=10ms−2
View SolutionTwo block A and B of equal masses are placed on rough inclined plane as shown in figure. When and where will the two blocks come on the same line on the inclined plane if they are released simultaneously? Initially the block A is √2 m behind the block B. Co-efficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2).
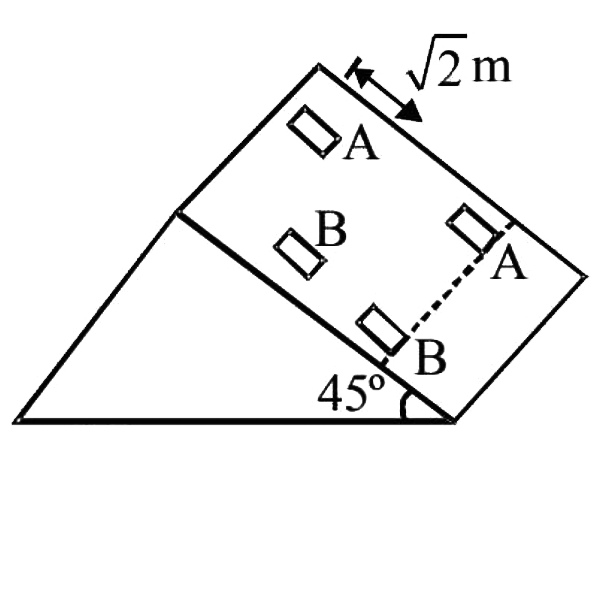
View Solution