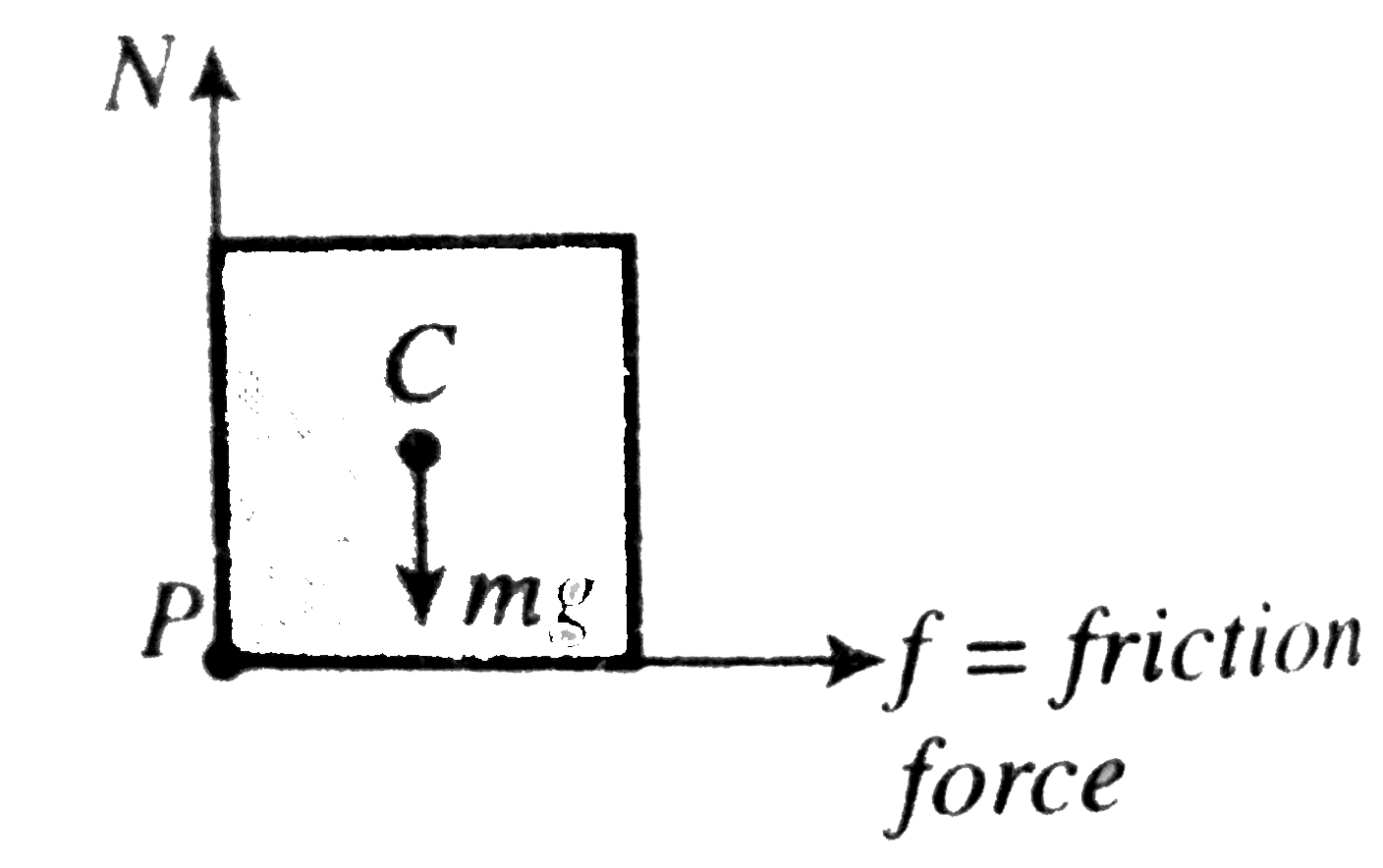
A block of mass height and width rests on a flat car which moves horizontally with constant acceleration a as shown in figure. Determine

a. the value of the acceleration at which slipping of the block on the car starts, if the coefficient of friction is .
b. the value of the acceleration at which block topples about , assuming sufficient friction to prevet slipping and
c. the shortest distance in which it can be stopped from a speed of with constant deceleration so that the block is not disturbed. The following data are given and
a. Maximum frictionnal force between block and car will be limiting force.

The maximum possible acceleration of block can be
if acceleration of car, exceeds this value slipping will start between the block and the car.
b. In the case when the block is about to topple about , normal reaction will pass through . The friction will be static nature.
............i
.......ii
the block topples when torque of f about exceeds the torque of .
The block topples when torqe of f about exceeds the torque of .
In case of the limiting value
or
or
so, if the acceleration of car exceeds this value the block will topple about .
c. the maximum acceleration /retardation at which the block is not disturbed, is the smaller of the two values, obtained above i.e,
Hence the maximum retardation can be
Now using
Initial velocity
or
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.1
Explore 6 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.2
Explore 17 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
Find the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
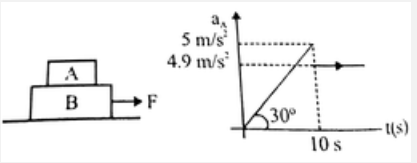
View SolutionAcceleration of block A varies with time as shown in figure the value of coefficient of kinetic friction between block A and B is
View Solution
Knowledge Check
A force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
AF−μmgMBzeroCmay be (A) or (B)DNone of theseA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isAμgBμMmgCμmMgDgμTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
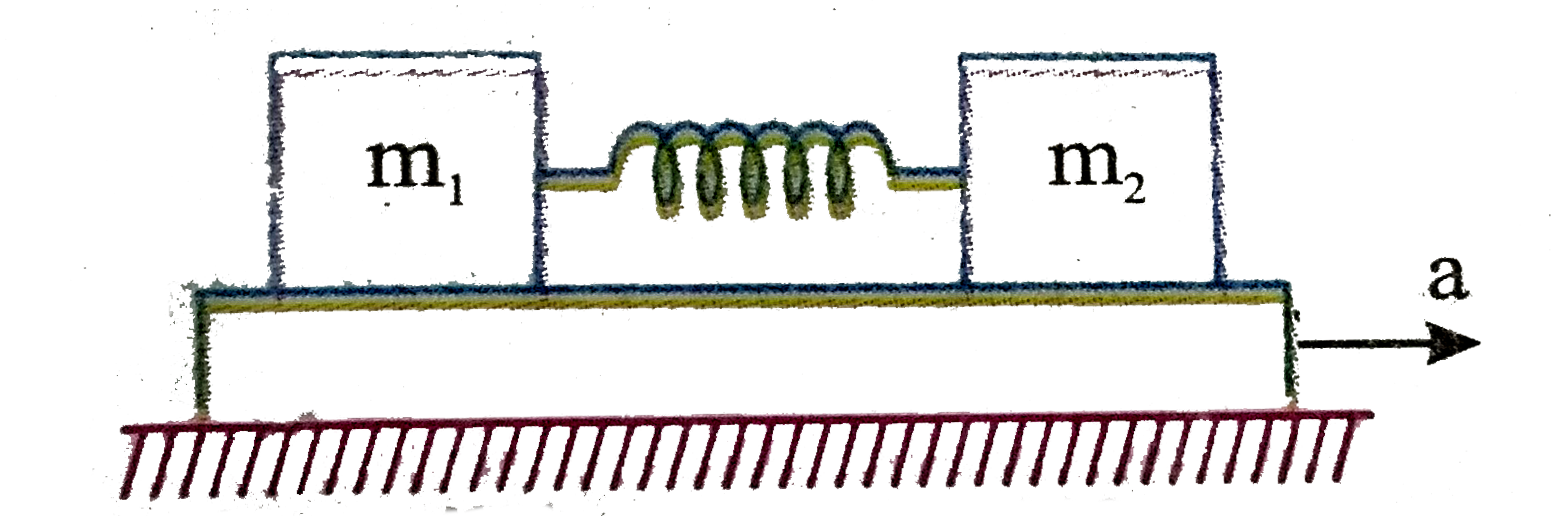 Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.
Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.
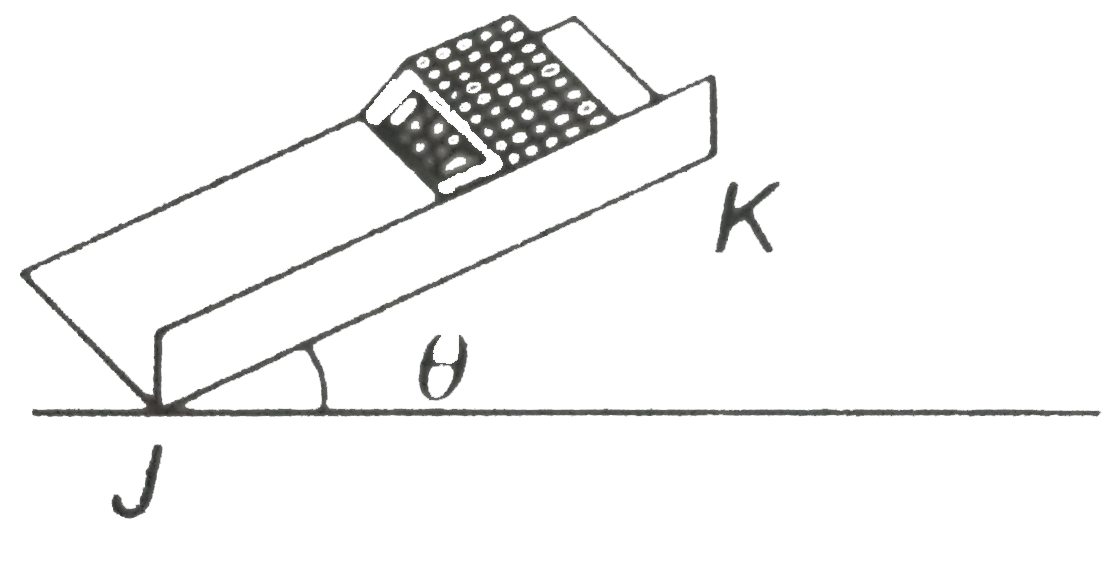
A cubical block of mass m is sliding on an inclined right angle trough as shown in the figure. If coefficient of friction is μ , find the acceleration of the block.
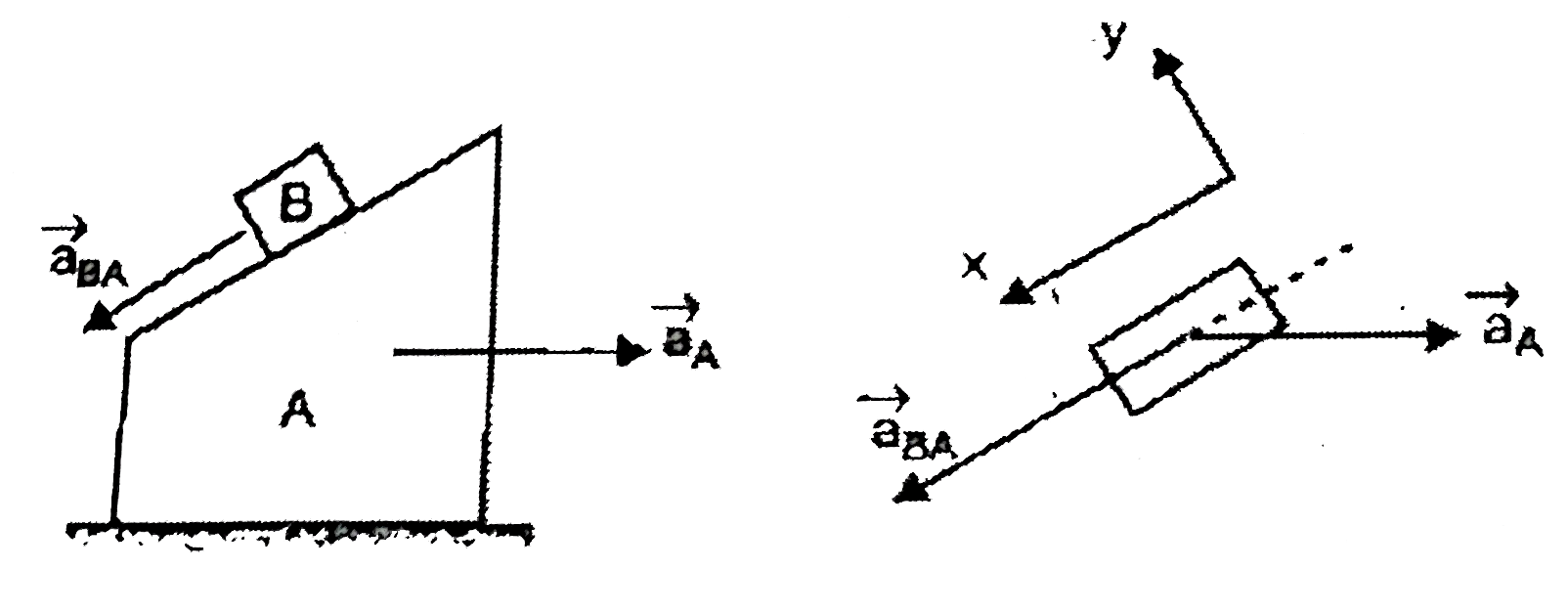
View SolutionThe block B starts from rest and slides on the wedge A which can move on a horizontal surface, Neglecting friction, determine (a) the acceleration of wedge, (b) the acceleration of the block relative to the wedge.
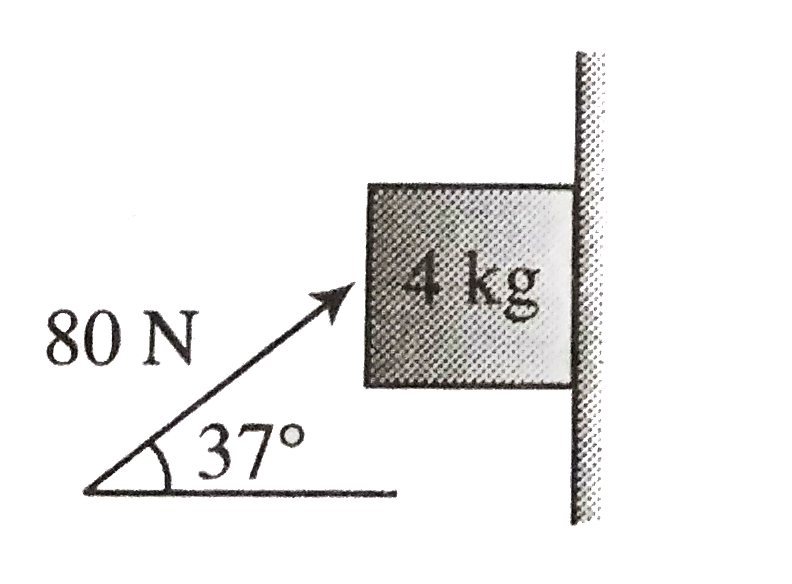
View SolutionA block of mass 4kg is pressed againest the wall by a force of 80N as shown in figure Determine the value of the friction force and block's acceleration (Take μs=0.2,μs=0.15)
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then
Acceleration of lower block is

View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block is
View Solution

