□ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE×BE=CE×TE.

segAB∣∣segCD
…..(Opposite sides of parallelogram are parallel)
i.e. set AT∣∣ seg CD ……….(A−B−T)
Line TD in the transversal,
∴∠ATD≅∠CDT …..(Alternate angles)
i.e ∠BTE≅∠CDE……..(A−B−T,T−E−D)..1
In ΔBET and ΔCED .....[From 1]
∴ΔBET~ΔC........(Vertically opposite angles)
:ΔBET~ΔCED ........(AA test of similarity)
∴BECE=TEDE....(Corresponding sides of similar triangles are in proportion)
∴BE×DE=CE×TE.
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - CHALLENGING QUESTIONS
8 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE
15 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)
3 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
□ABCD is a parallelogram. Point E is on side BC. Line DE intersects ray AB in point T. Prove that DE×BE=CE×TE.
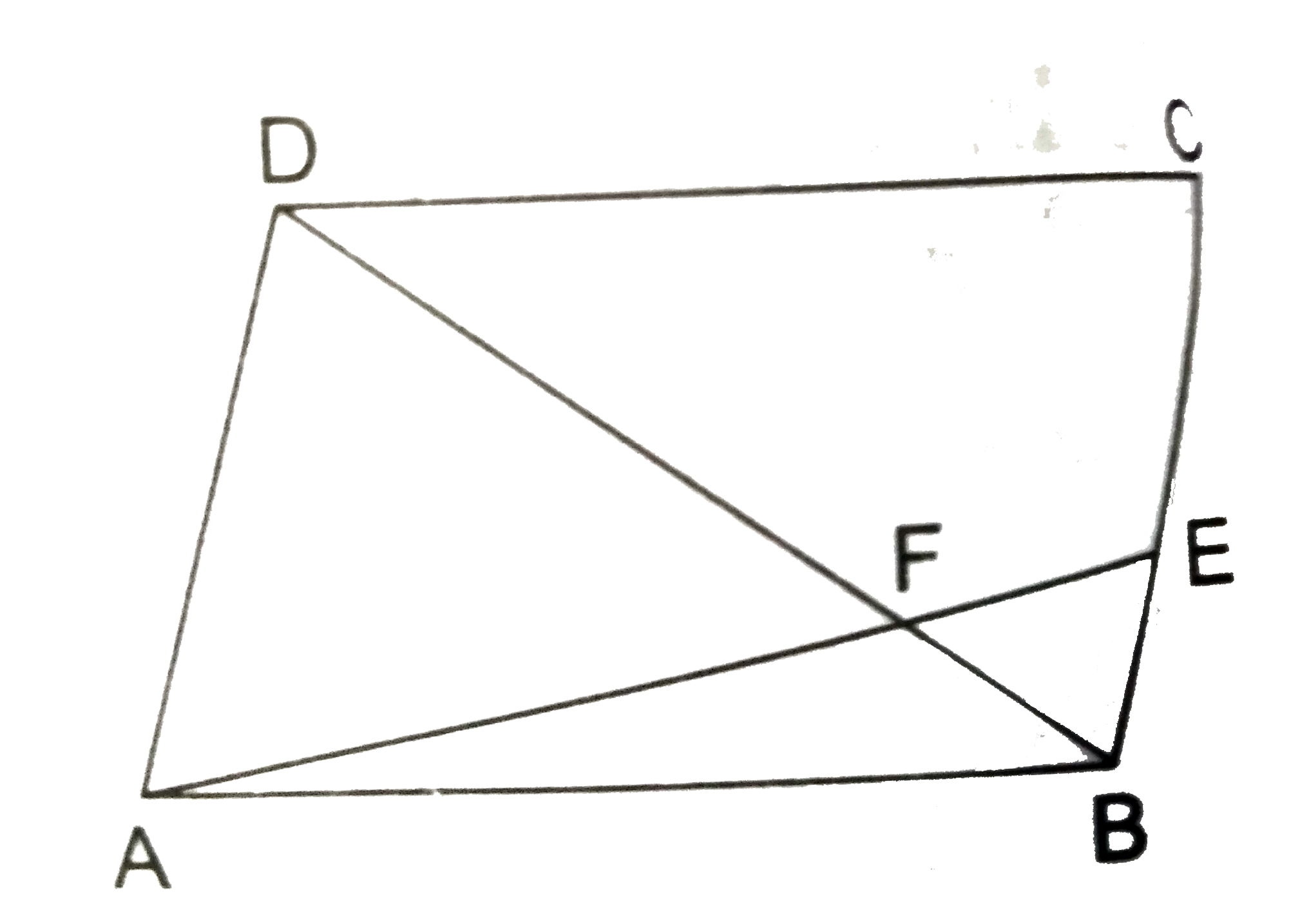
View SolutionABCD is a parallelogram and E is a point, on BC. If the diagonal BD intersects AE at F, prove that AF×FB×EF×FD.
View SolutionIn the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

View SolutionIn a parallelogram ABCD, the bisector of ∠A bisects the line Bcat point X. Prove that AD = 2AB.
View SolutionABCD is a parallelogram. AB is produced to E so that BE=AB . Prove that ED bisects BC.
View SolutionIf ABCD is a parallelogram, E is the mid-point of AB and CE bisects ∠BCD, then ∠DEC is
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionThe diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
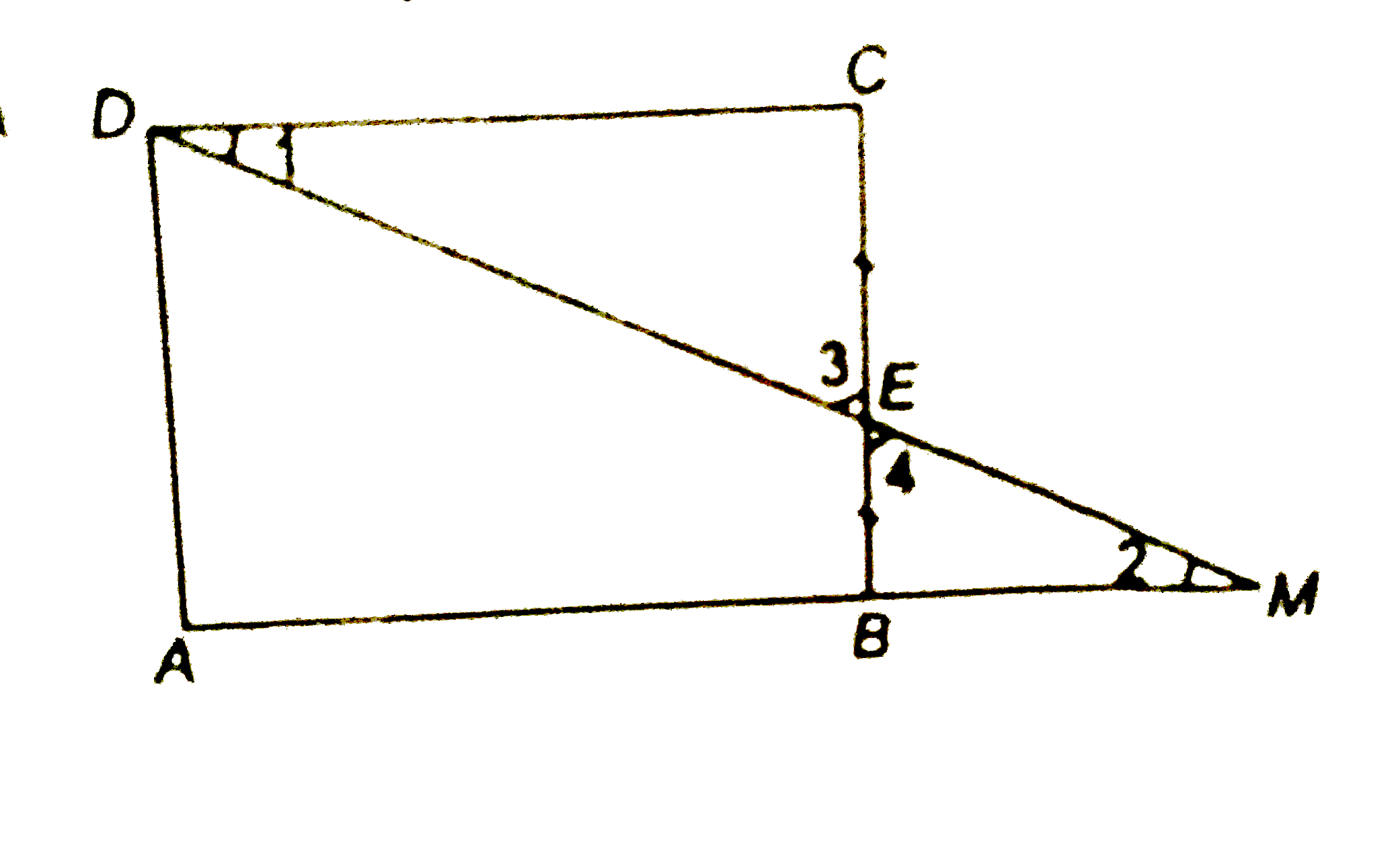
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
View Solution
