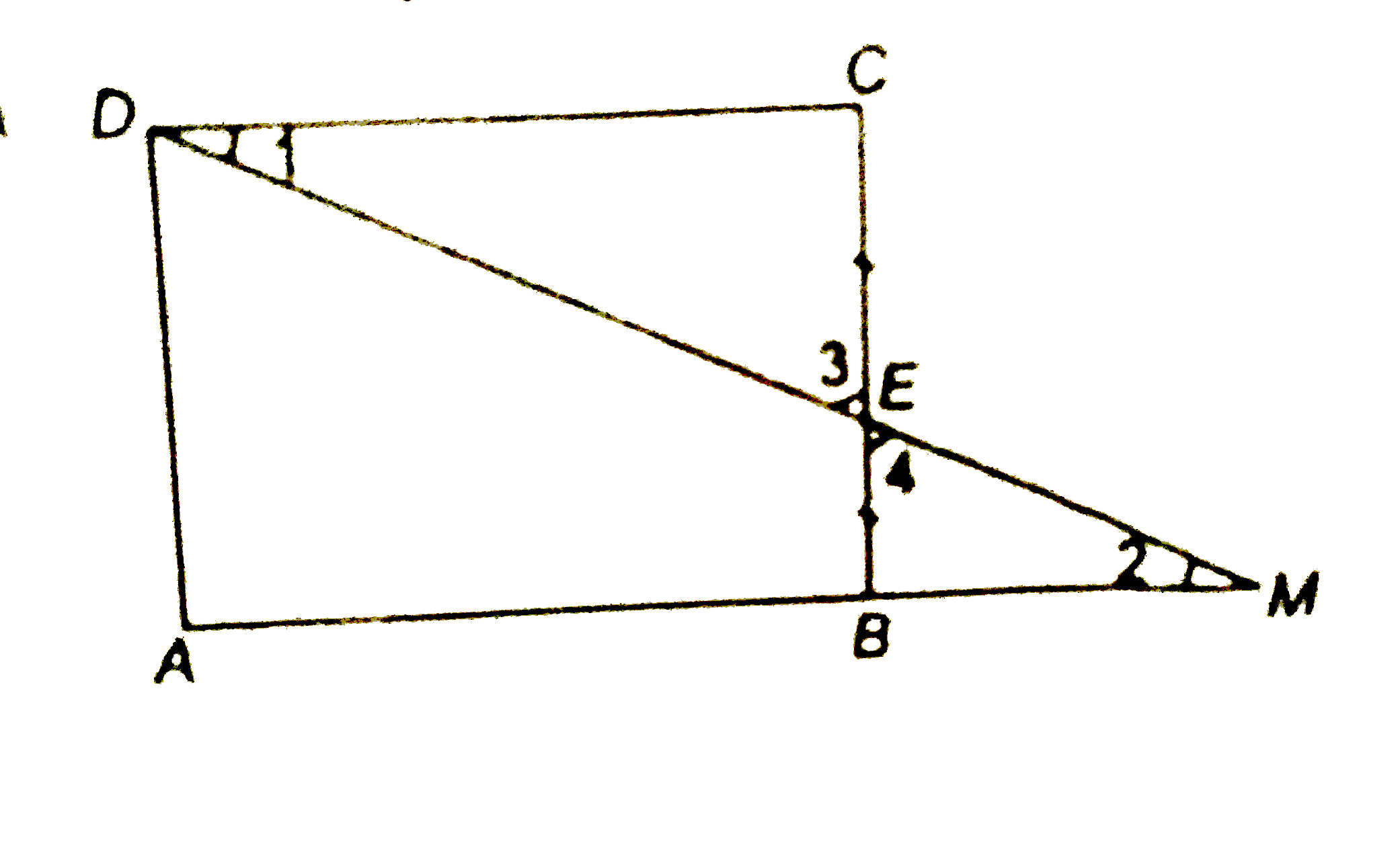
In the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
Video Solution
Text Solution
(i) Since ABCD is a parallelogram
∴ABM||DC
∴∠1=∠2 (alternate angles)
Now, in ΔDCE and ΔMBE
∴⎧⎪⎨⎪⎩∠1=∠2(proved above)∠3=∠4(vertically opposite angles)CE=BE(given as E is the mid-point)
∴ΔDCE≅ΔMBE (AAS) Hence Proved.
(ii) Therefore, DC=MB (c.p.c.t.)
But DC=AB (opposite sides of a parallelogram are equal)
∴AB=MB Hence Proved.
(iii) Now, AM=AB+BM
=DC+DC (poved above)
=2DC Hence Proved.
|
Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Problems From NCERT/exemplar
Explore 5 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Exercise 7a
Explore 35 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHANChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
Knowledge Check
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2In the adjoining figure a parallelogram ABCD is shown .
AB=24 cm and AO=BO=13 cm. Find BC :
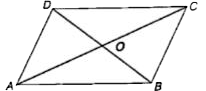 A8 cmB10 cmC11 cmDnone of these
A8 cmB10 cmC11 cmDnone of theseABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AA)AN=√3ABBB)AN=2ABCC)AN2=32AB2DD)AN2=2AB2
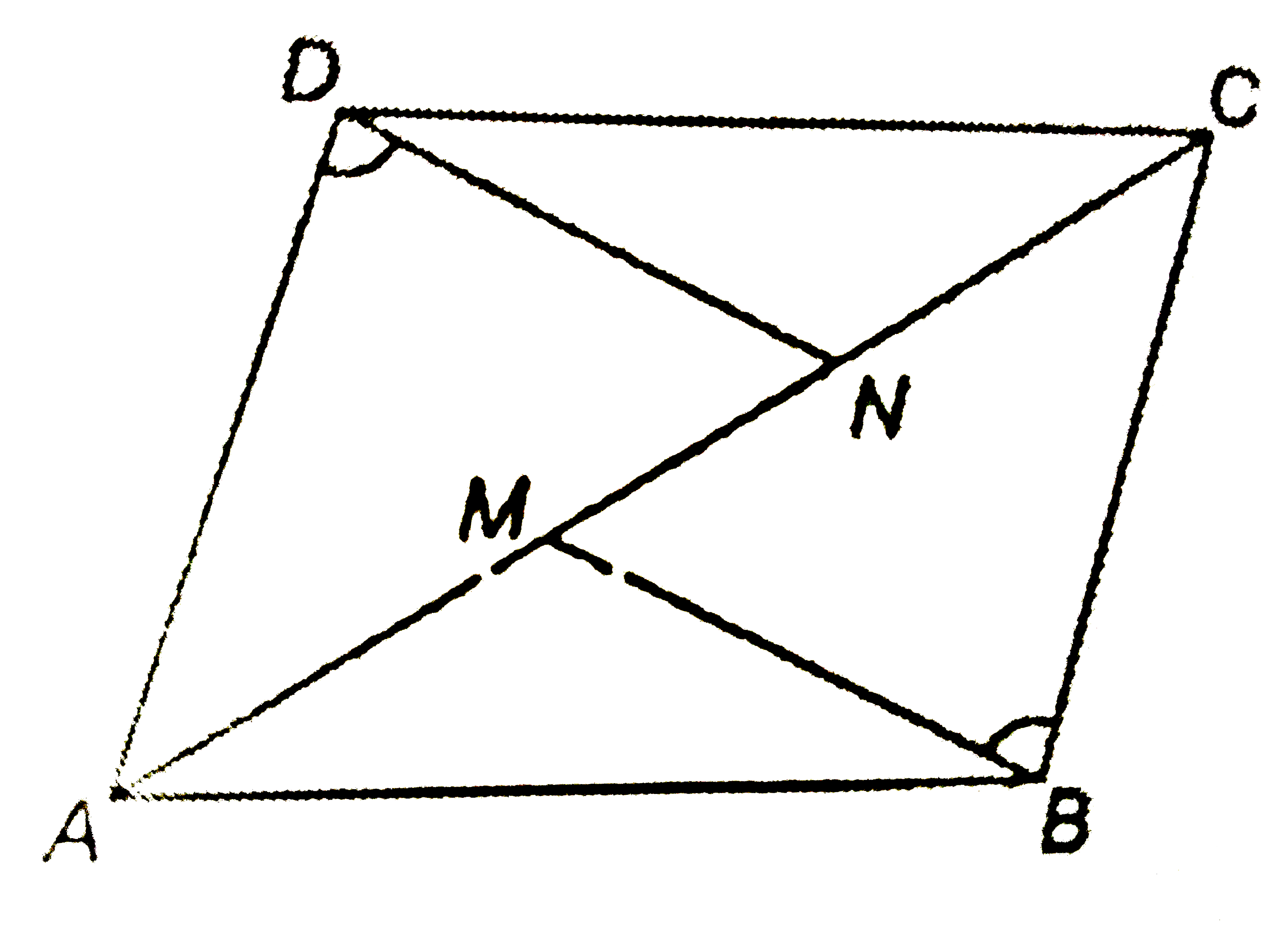
In the adjoining figure, ABCD is a parallelogram. If ∠MBC=∠NDA, prove that AM=NC.
View SolutionIn the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
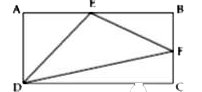
View SolutionIn the given figure ABCD is a parallelogram in which AB||CD and E and F are the mid points of AB and BC respectively. What is the area of ∠BEF?
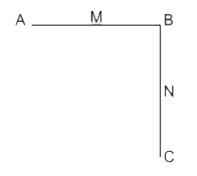
View SolutionIn the give figure AB = BC, M is the mid point of AB and N is the mid point of BC, Show that AM = NC
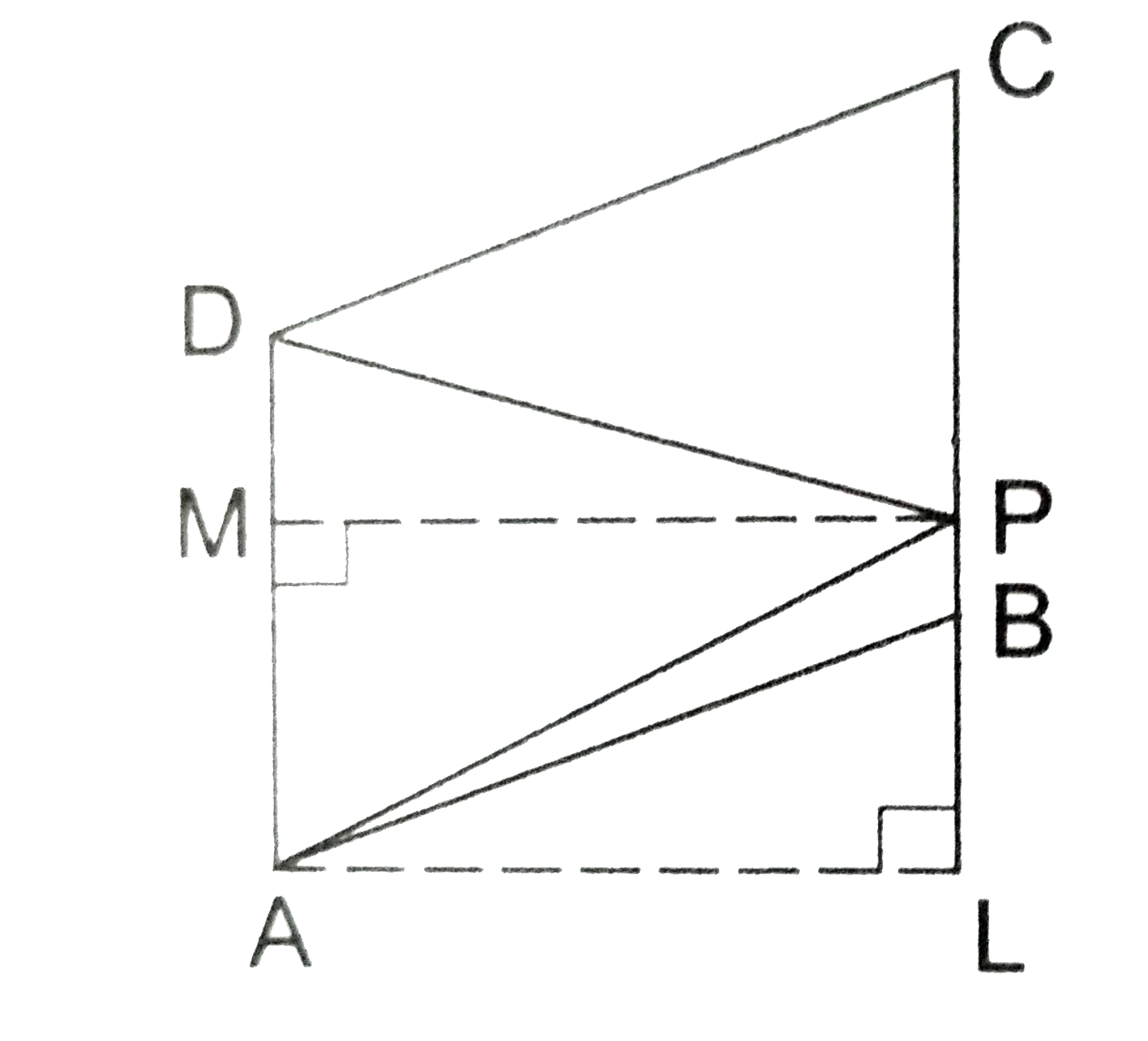
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View Solution


