Given: In trapezium PQRS, sides PQ∣∣ sides SR,AR=5AP,AS=5AQ, then prove that SR=5PQ.
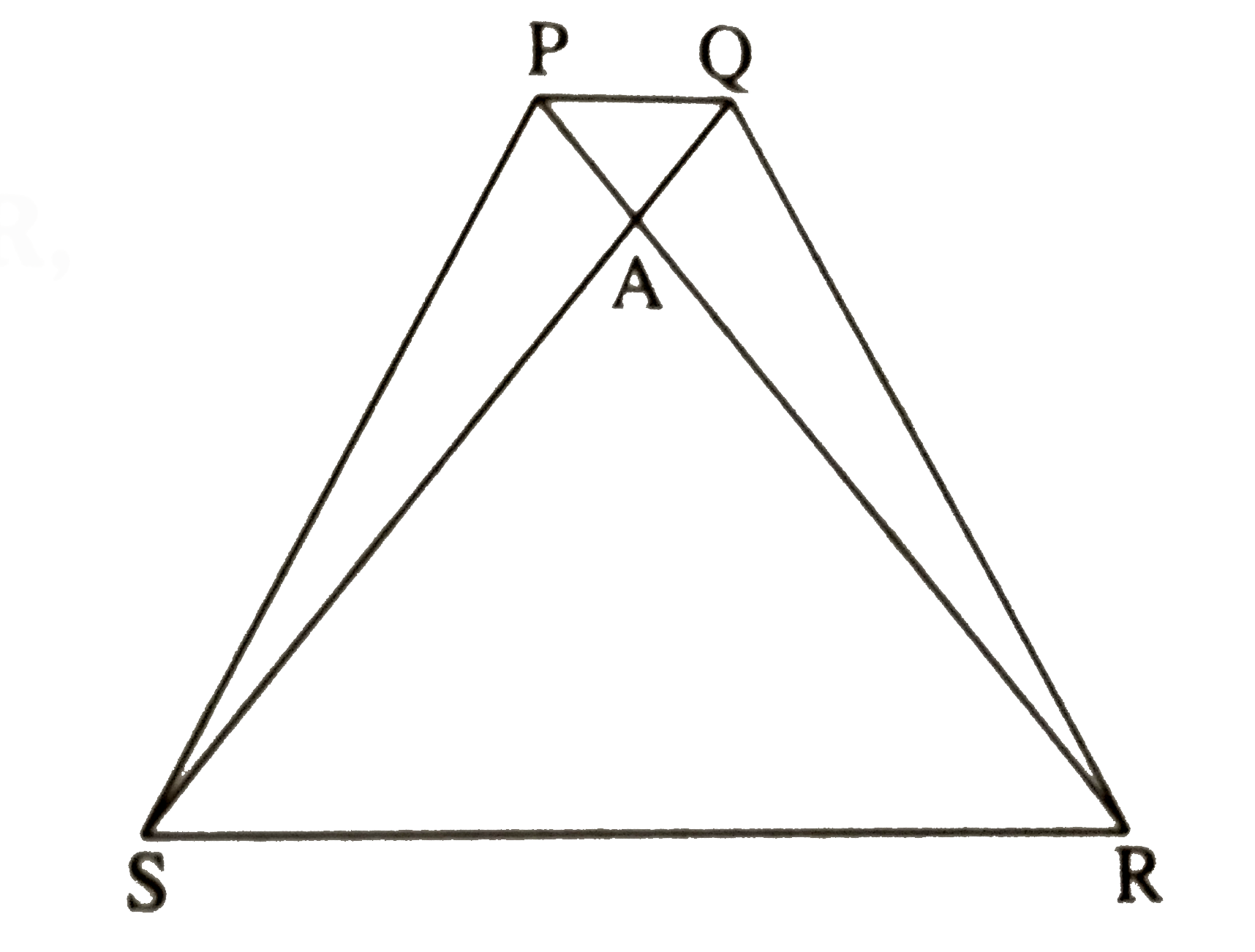
Side PQ∣∣ side SR and line QS is the transversal
∴∠PQS≅∠RSQ ……(Alternate angles)
i.e. ∠PQA≅∠RSA..(Q−A−S)…….1
In ΔPQA and ΔRSA
∠PQA≅∠RSA……[From 1]
∠PAQ≅∠RAS. (Vertically opposite angles)
∴ΔPQA~ΔRSA...(AA test of similarity)
∴PQRS=AQAS=APAR
............(Corresponding sides of similar triangles are in proportion) .......2
AR=5AP....(Given ) ...........3
Substituting 3 in 2 we get
∴PQSR=AQAS=AP5AP
∴PQSR=AQAS=15............4
∴PQSR=15........[From 4]
∴SR=5PQ
Alternative method
AR=5AP .(Given)
∴ARAP=51 ......1
AS=5AQ........(Given)
∴ASAQ=51......2
In ΔRAS and ΔPAQ.
ARAP=ASAQ ......[From 1 and 2]
∠RAS≅∠PAQ...[vertically opposite angles]
∴ΔRAS~ΔPAQ..(SAS test of similarity)
∴ARAP=SRQP ........[Corresponding sides of similar triangles are in proportion]
∴51=SRQP [From 1 ]
∴SR=5PQ
Topper's Solved these Questions
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:CHALLENGING QUESTIONS
Explore 8 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:MCQ TYPE
Explore 15 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:2.5 (4 mark each)
Explore 3 Videos
- QUADRATIC EQUATIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUADRATIC EQUATIONS Exercise:ASSIGNEMENT 2.4
Explore 8 Videos
- STATISTICSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:STATISTICSExercise:EXAMPLES FOR PRACTICE (MCQs)
Explore 35 Videos
Similar Questions
Given : In trapezium PQRS,sPQ∣∣sSR,AR=5AP,AS=5AQthen prove that,SR=5PQ
View SolutionGiven : In trapezium PQRS, side PQ||SR, AR = 5 AP, AS = 5 AQ, then prove that SR=5 PQ.
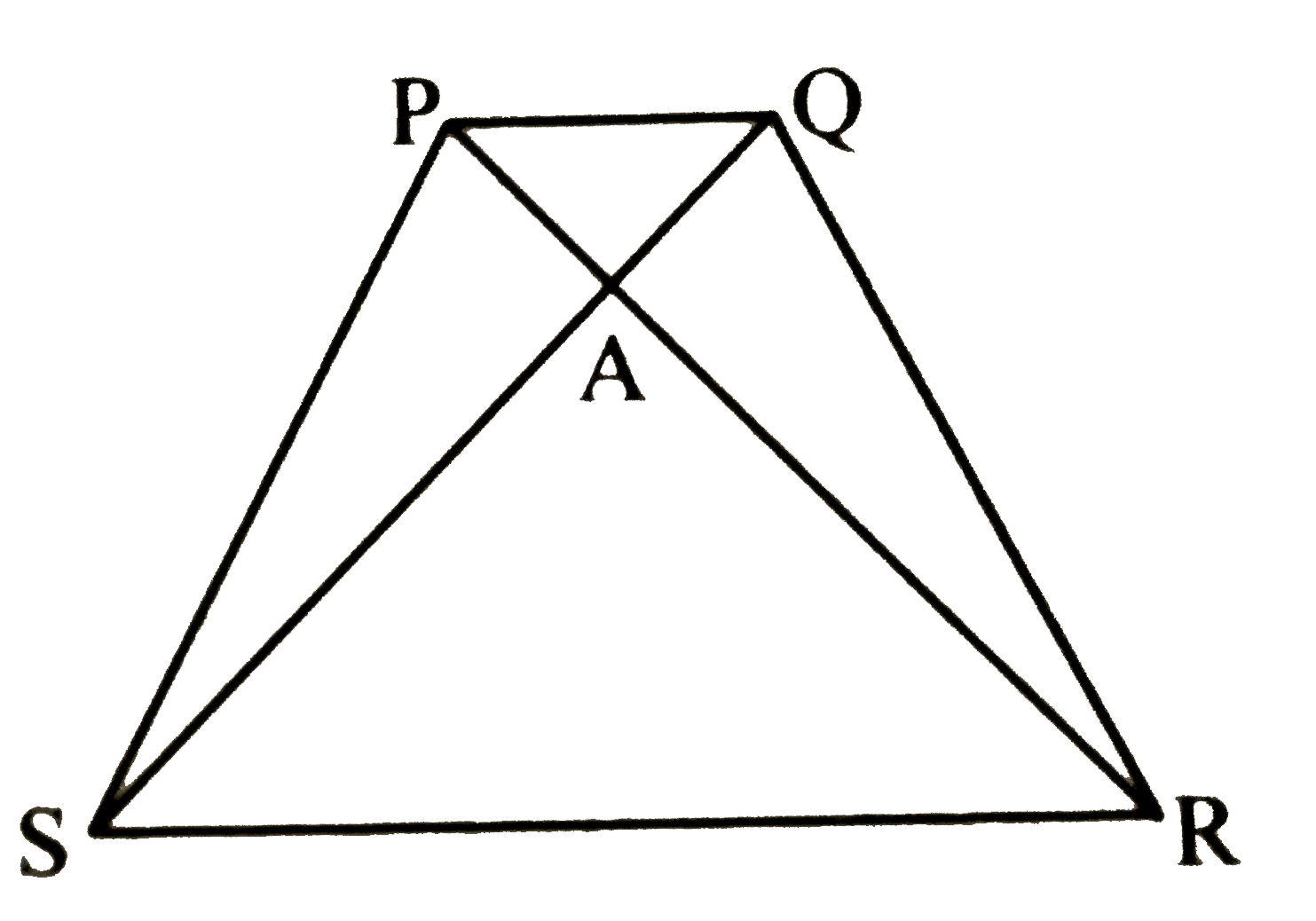
View SolutionIn trapezium PQRS, side PQ∣∣ side SR, AR=5AP, AS=5AQ then prove that SR=5PQ by completing the following activity.
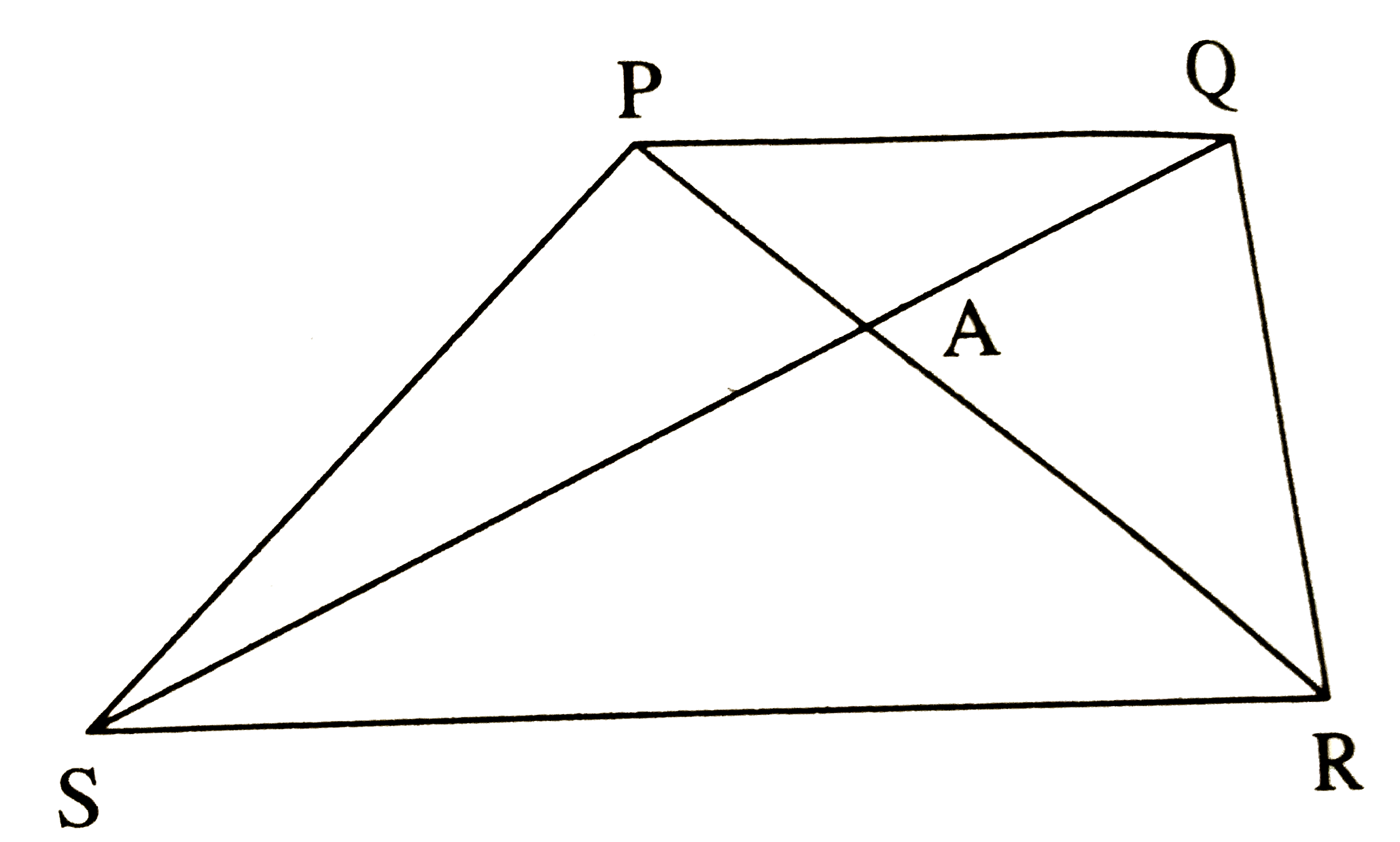
In ΔPQA and ΔRSA,
∠PQA≅∠RSA……(□)
∠PAQ≅∠RAS....(□)
∴ΔPQA~ΔRSA ......(□)
PQSR=□AR.........(Corresponding sides of similar triangles).....(1)
Substituting AR=5AP in (1)
∴PQSR=□5AP
∴PQSR=□5
∴SR=5PQ
View Solution∠PQR=∠PRS, then prove that ∠PQS=∠PRT
View SolutionIn trapezium ABCD side AB∣∣ side PQ∣∣ side DC,AP=15,PD=12,QC=14, find BQ.
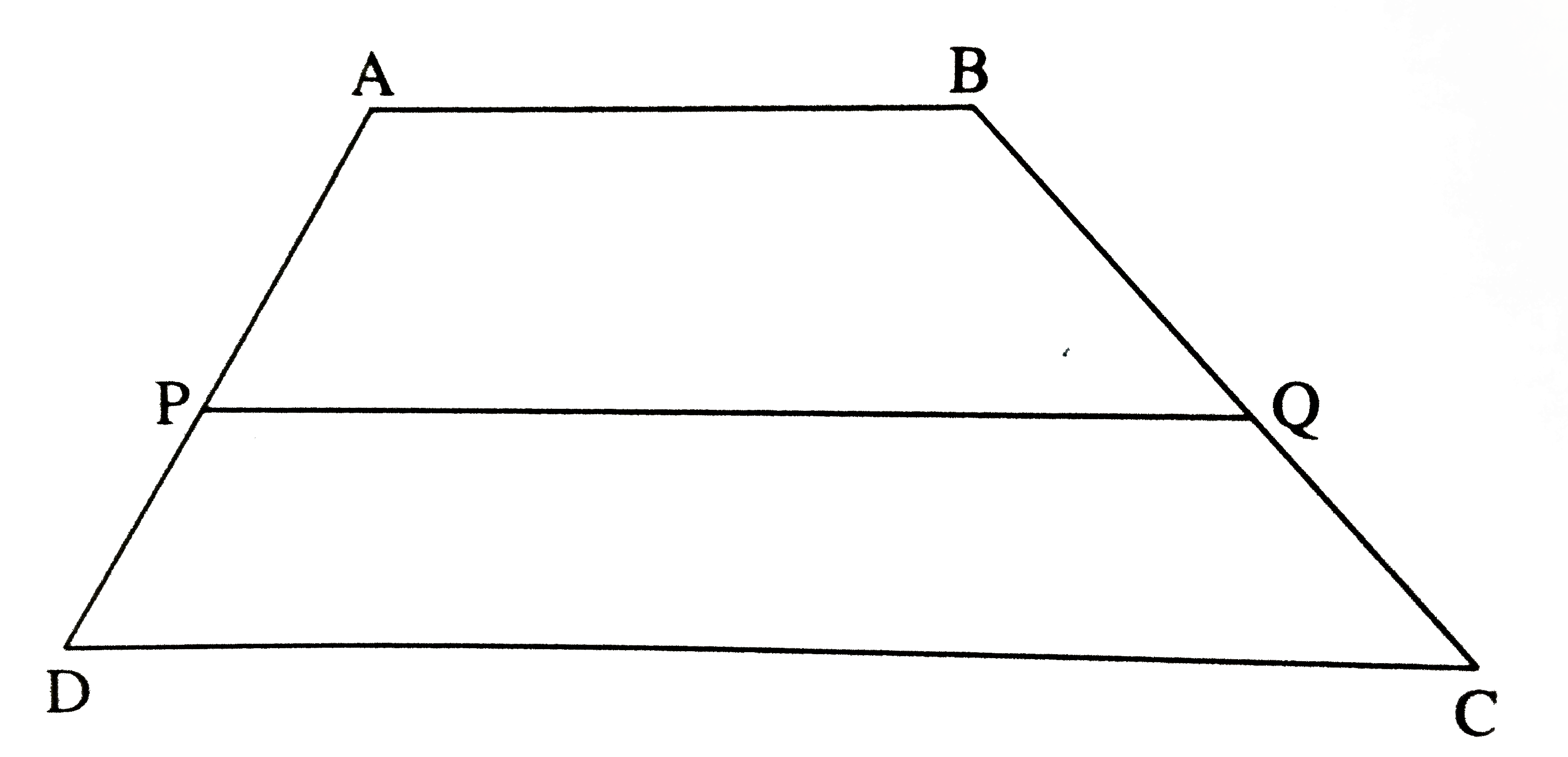
View SolutionIn trapezium PQRS,side PQ∣∣ sideSR. Diagonals PR and QS intersect each other at point M. PQ=2RS. Prove that PM=2RM and QM=2SM.
View SolutionIn the figure given below if PQRS is a parallelogram and AB |PS then prove that OC ||SR.
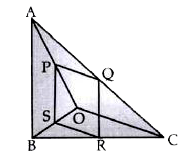
View SolutionIn the given figures, if PQRS is a parallelogram and AB||PS, then prove that OC||SR.
View SolutionIf Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
View SolutionIn the trapezium PQRS, PQ is parallel to RS and the ratio of the areas of the triangle POQ to triangle ROS is 225:900 . Then SR= _________.
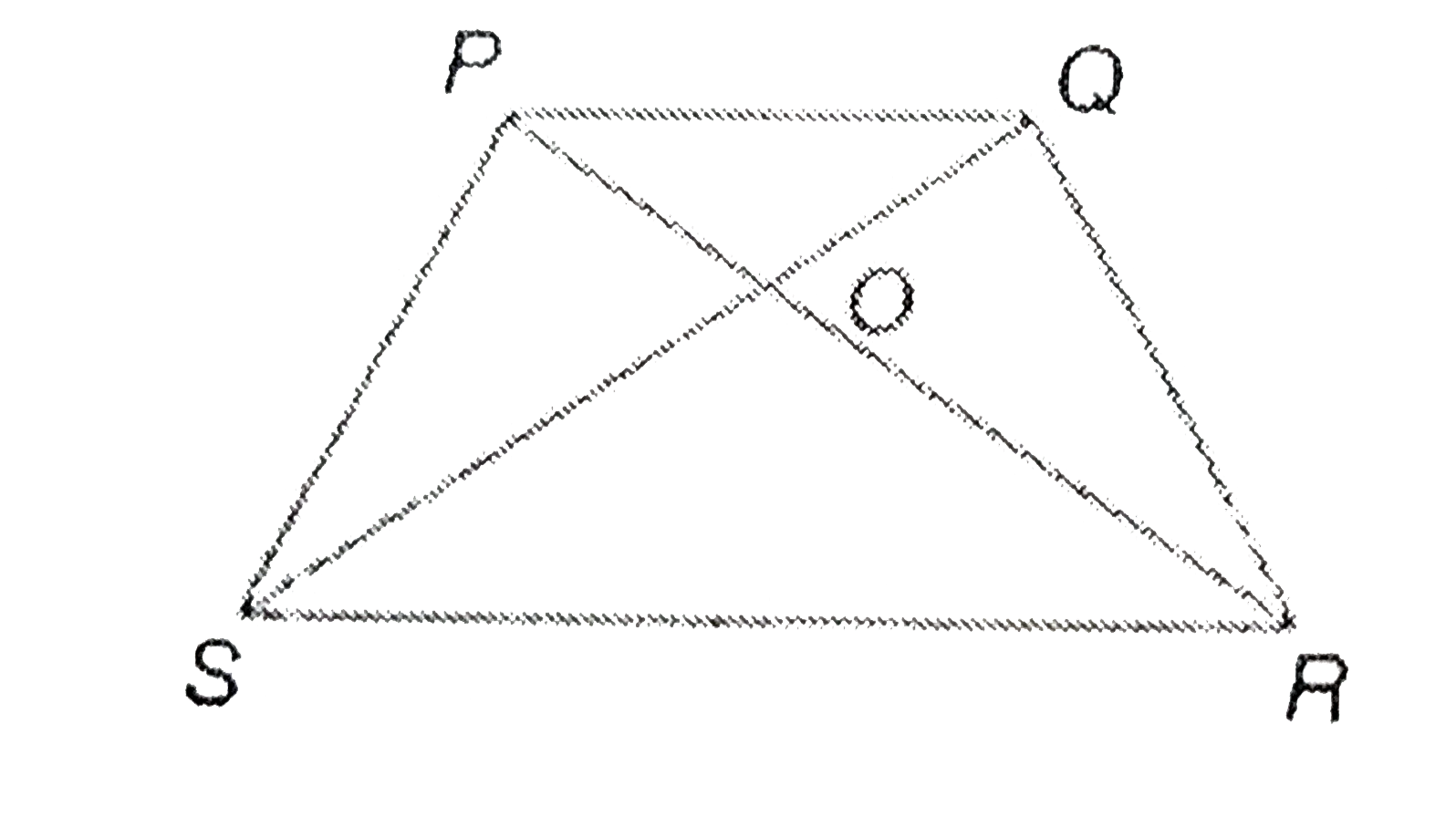
View Solution