In the figure X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ∣∣ set DE, set QR∣∣ set EF. Fill in the blanks to prove that set PR∣∣ seg DF.
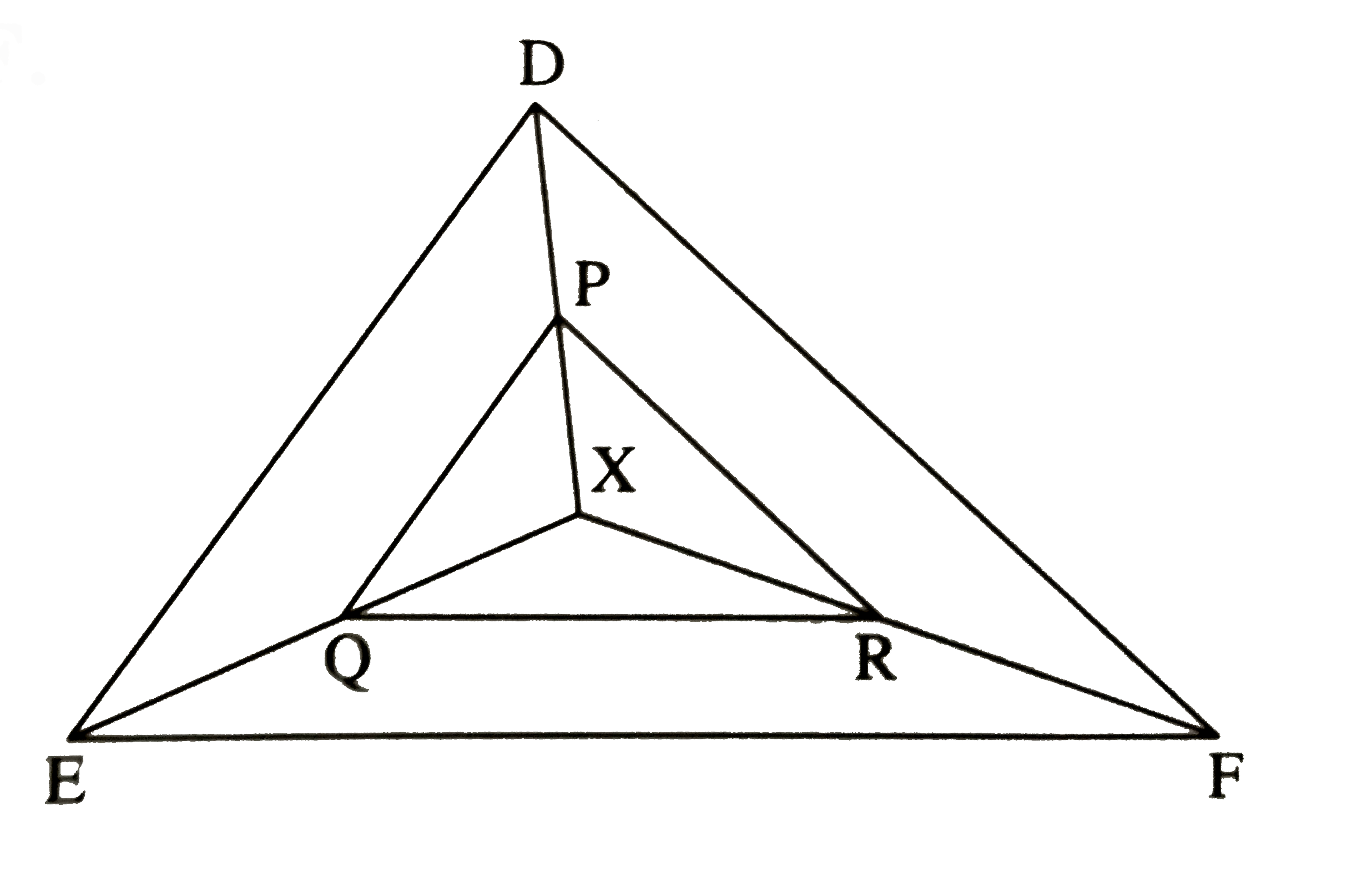
In ΔXDE,PQ∣∣DE
∴XP□=□QE=……………………..(□)
………….(I) (Basic proportionality theorem)
In ΔXEF,QR∣∣EF……(□)
∴□□=□□
….(II) (□)
∴□□=□□....[From I and II]
∴ set PR∣∣ set DF
gt......(Converset of basic proportionality theorem)
In ΔXDE,PQ∣∣DE...........Given
∴XPPD+XQQE
......I (Basic proportionality theorem)
In ΔXEF,QR∣∣E Given
∴XQQE=XRRF
...II (Basic proportionality theorem)
∴XPPD=XRRF.........From I and II
∴ set PR∣∣ seg DF
..(Covnerset of basic proportionality theorem)
Topper's Solved these Questions
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:CHALLENGING QUESTIONS
Explore 8 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:MCQ TYPE
Explore 15 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:2.5 (4 mark each)
Explore 3 Videos
- QUADRATIC EQUATIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUADRATIC EQUATIONS Exercise:ASSIGNEMENT 2.4
Explore 8 Videos
- STATISTICSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:STATISTICSExercise:EXAMPLES FOR PRACTICE (MCQs)
Explore 35 Videos
Similar Questions
S is any point in the interior of a △PQR . Prove that SQ+SR<PQ+PR
View SolutionIn a △PQR mark
the points X, Y, Z in the interior of △ PQR
View SolutionIf Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
View SolutionTake any point O in the interior of a triangle PQR. Is (i) OP+OQ>PQ? (ii) OQ+OR>QR? (iii) OR+OP>RP?
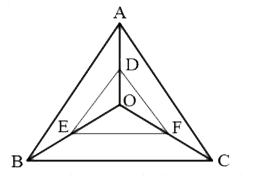
View SolutionIn the figure, a point O inside △ABC is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC.
View SolutionIn the figure ΔPQR is an equilateral triangle. Point S is on seg QR such that
QS=13QR.
Prove that : 9PS2=7PQ2

View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

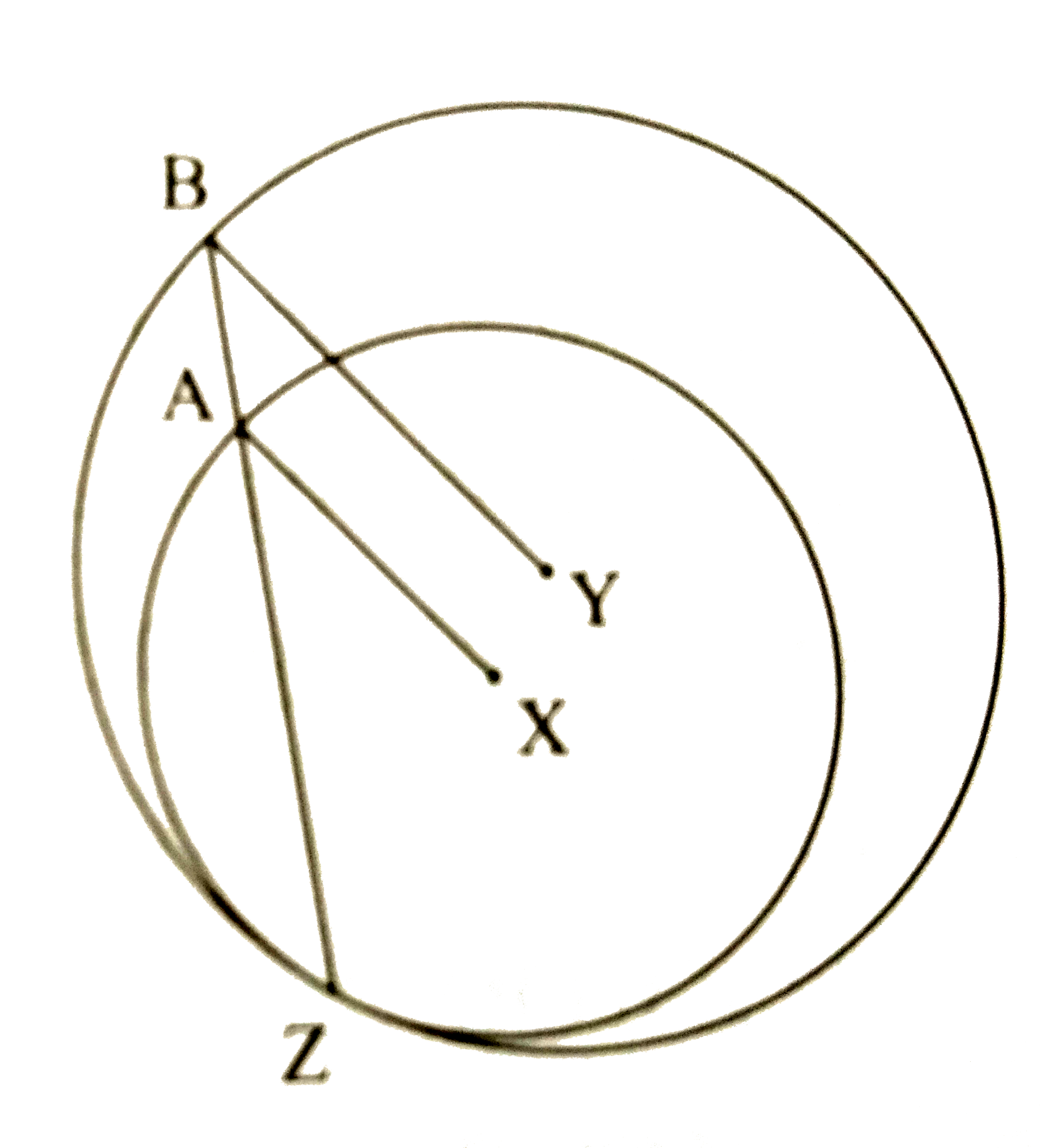
View SolutionIn the figure , circles with centres X and Y touch internally at point Z. Seg BZ is the chord of bigger circle and it intersects smaller k circle at point A.
Prove that seg AX∣∣ seg BY.
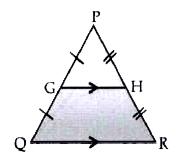
View SolutionIn the given figure G is the mid-point of the side PQ of ΔPQR and GH || QR .Prove that H is the mid -point of the side PR of the triangle PQR .
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
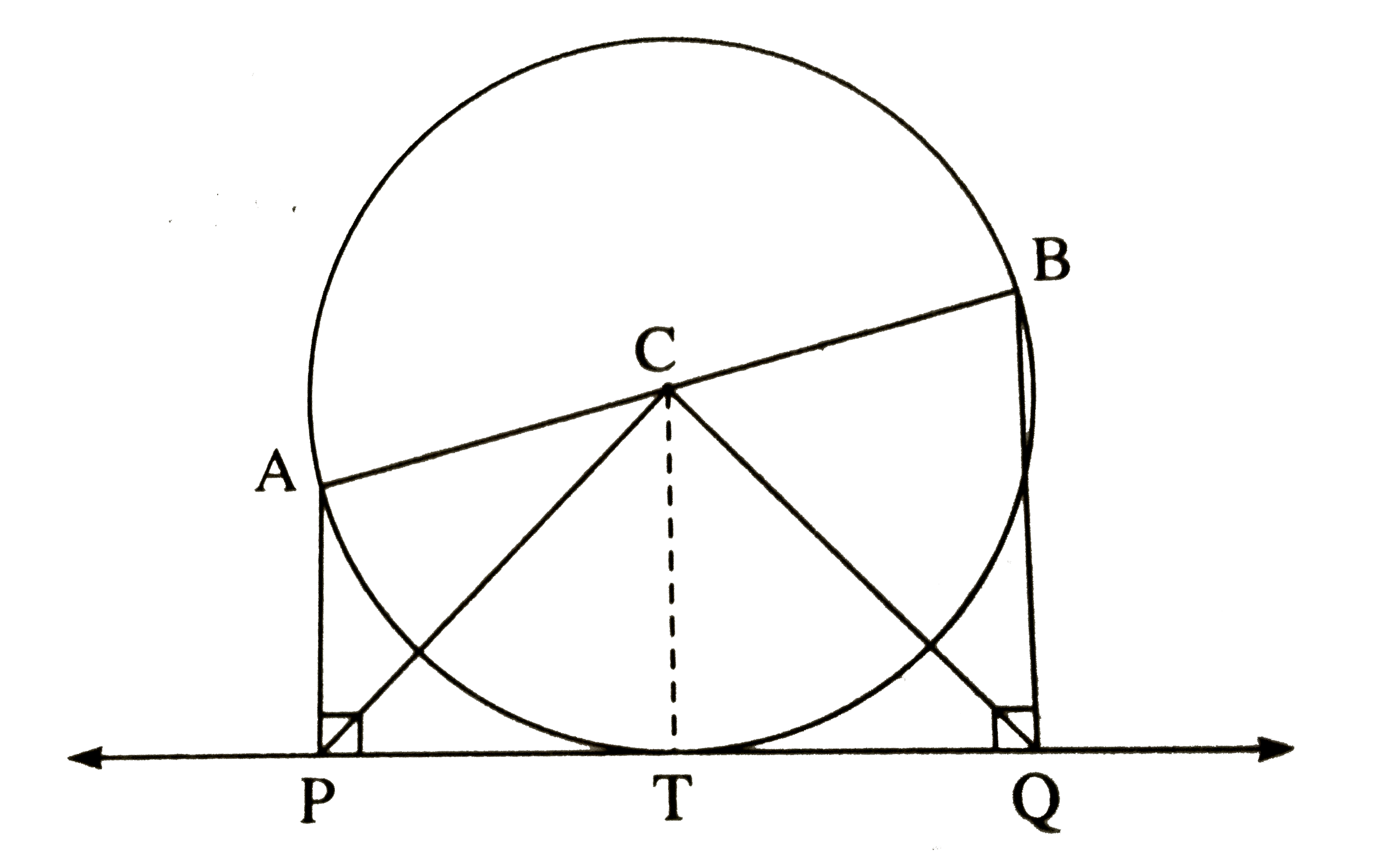
View Solution

