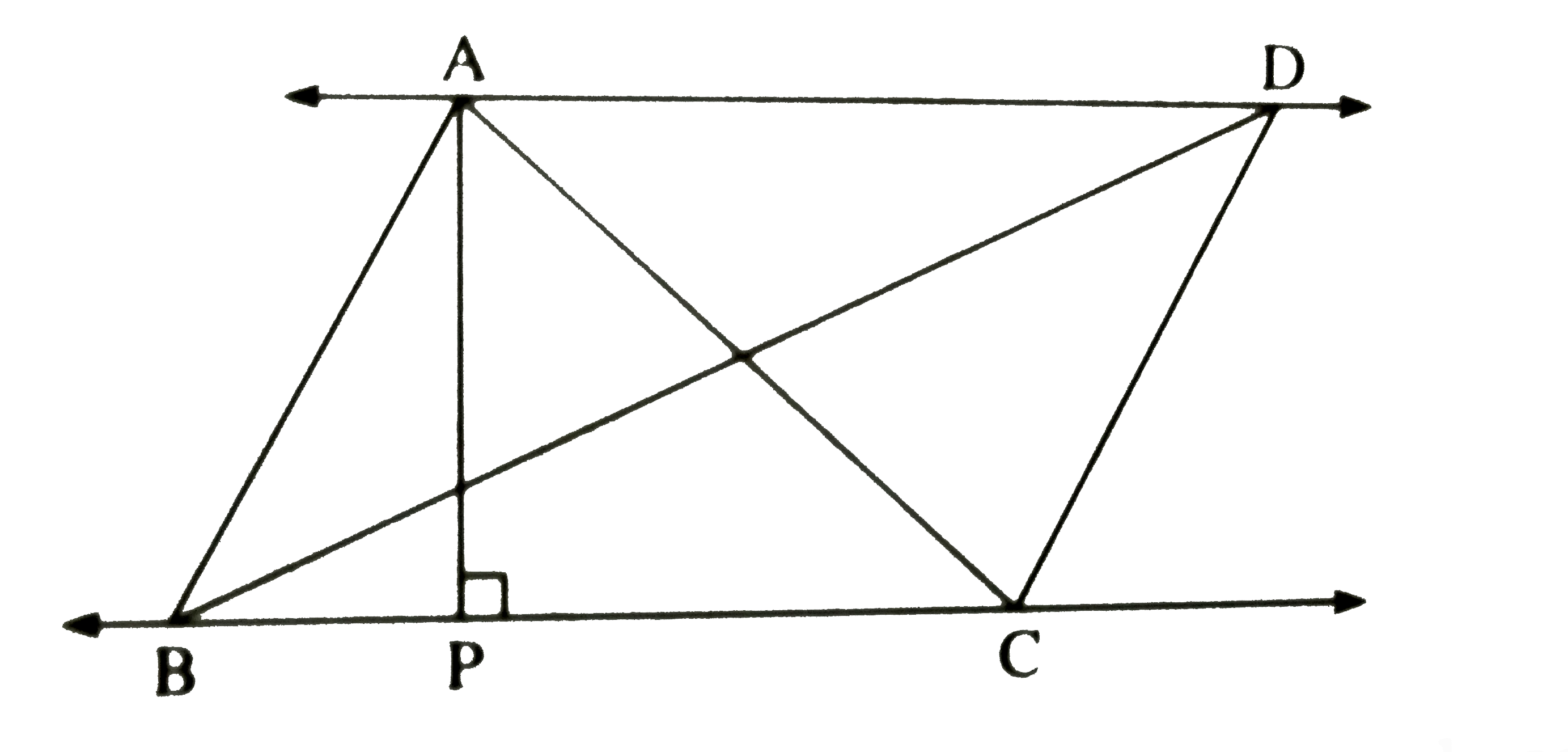
In the adjoining figure PQ⊥BC,AD⊥BC, then find following ratios:
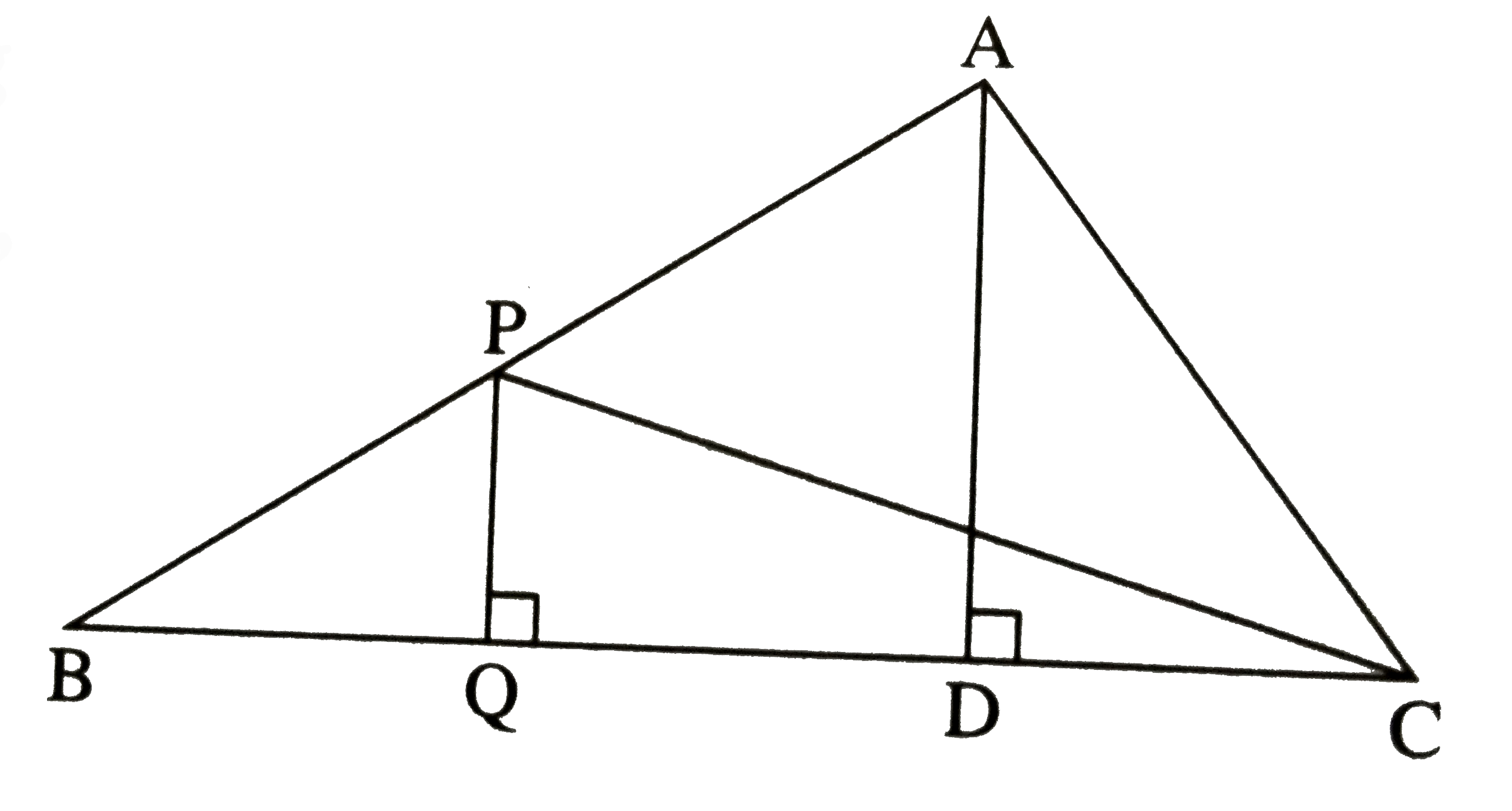
(i( A(ΔPQB)A(ΔPBC) (ii) A(ΔPBC)A(ΔABC)
(iii) A(ΔABC)A(ΔADC)(iv) A(ΔADC)A(ΔPQC)
ΔPQB and ΔPBC have same height PQ. Areas of triangles with equal heights are proportional to their corresponding bases.
∴A(ΔPQB)A(ΔPBC)=QBBC
(iii) ΔPBC and ΔABC have same base BC.
Area of triangles with equal bases are propoprtional to their corresponding heights.
∴A(ΔPBC)A(ΔABC)=PQAD
(iii) ΔBC and ΔADC have same height AD. Areas of triangles with equal heights are proportional to their corresponding bases.
∴A(ΔABC)A(ΔADC)=BCDC
(iv) Ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
∴A(ΔADC)A(ΔPQC)=DC×ADQC×PQ
Ans.
(i) A(ΔPQB)A(ΔPBC)=QBBC (ii) A(ΔPBC)A(ΔABC)=PQAD
(iii) A(ΔABC)A(ΔADC)=BCDC (iv) A(ΔADC)A(ΔPQC)=DC×ADQC×PQ
Topper's Solved these Questions
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:CHALLENGING QUESTIONS
Explore 8 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:MCQ TYPE
Explore 15 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:2.5 (4 mark each)
Explore 3 Videos
- QUADRATIC EQUATIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUADRATIC EQUATIONS Exercise:ASSIGNEMENT 2.4
Explore 8 Videos
- STATISTICSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:STATISTICSExercise:EXAMPLES FOR PRACTICE (MCQs)
Explore 35 Videos
Similar Questions
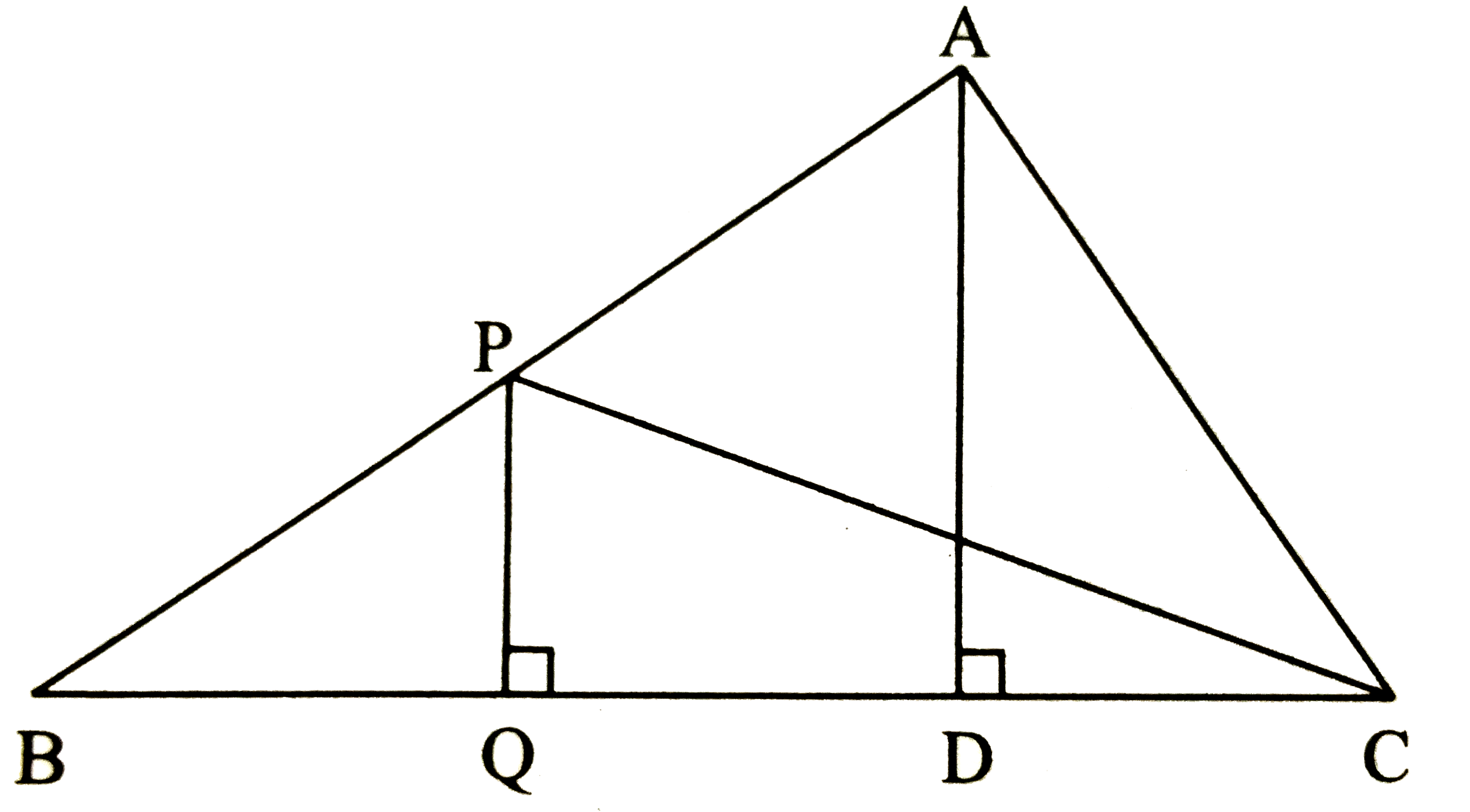
In adjoining figure, PQ⊥BC, AD⊥BC then find the following ratios.
(i)A(ΔPQB)A(ΔPBC) (ii)A(ΔPBC)A(ΔABC)
View SolutionIn ΔABC,B−D−C and BD=7,BC=20, then find followig ratios:
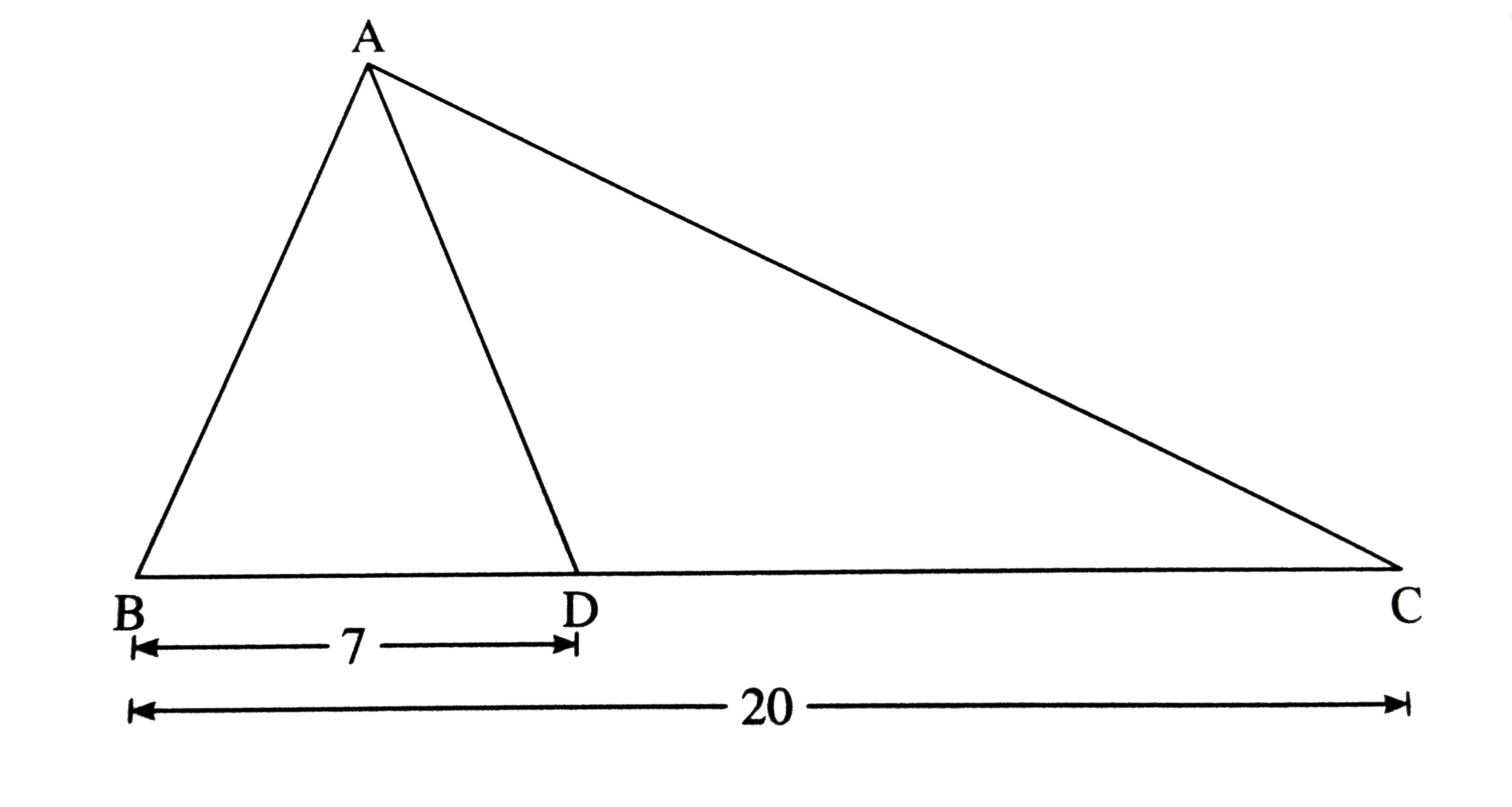
A(ΔABD)A(ΔADC)
A(ΔABD)A(ΔABC)
A(ΔADC)A(ΔABC)
View SolutionIn the adjoining figure, PQ⊥BC,AD⊥BC, then find ratio
A(ΔPQB)A(ΔPBC).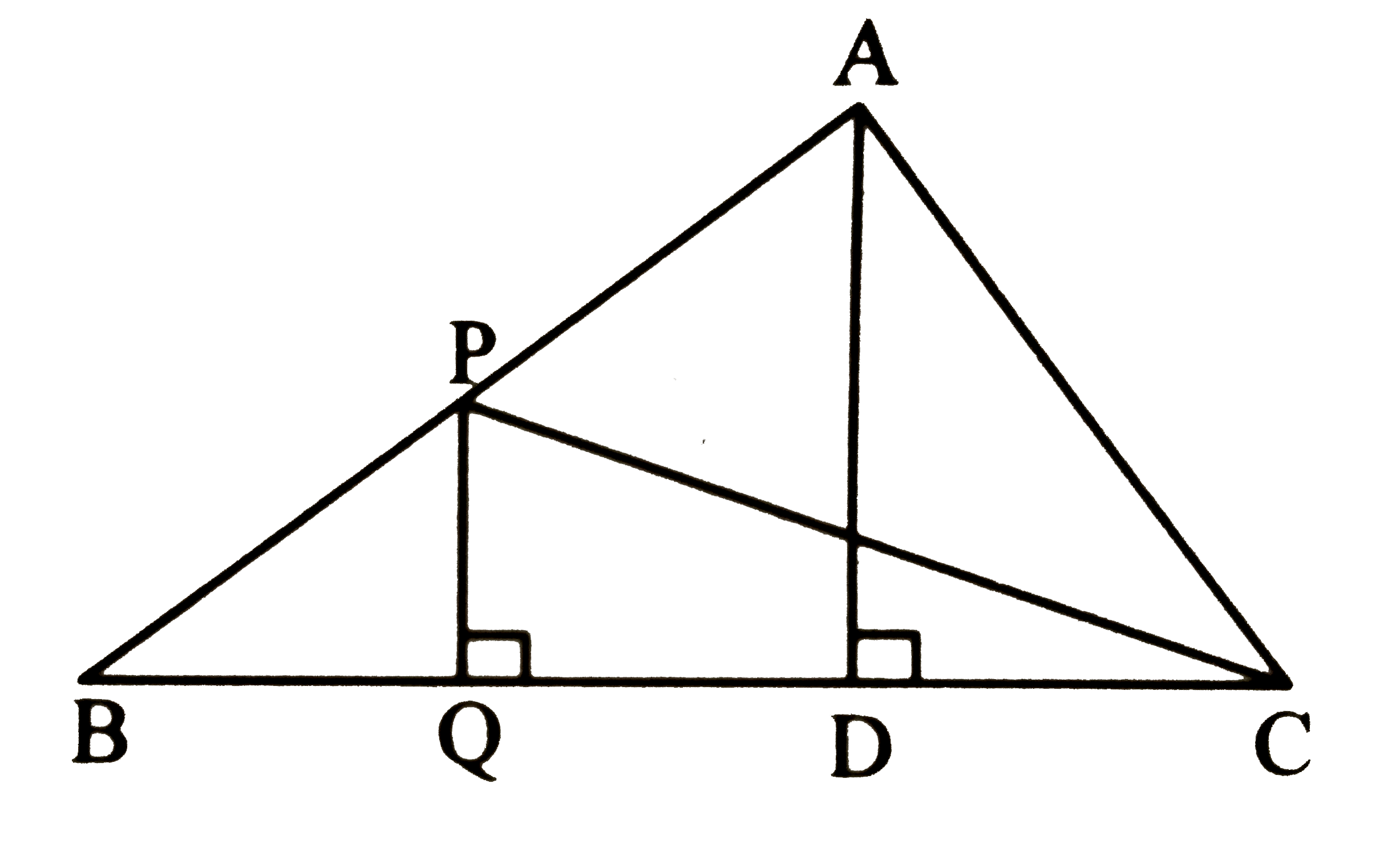
View SolutionIn the adjoining figure, PQ⊥BC,AD⊥BC, then find ratio
A(ΔADC)A(ΔPQC)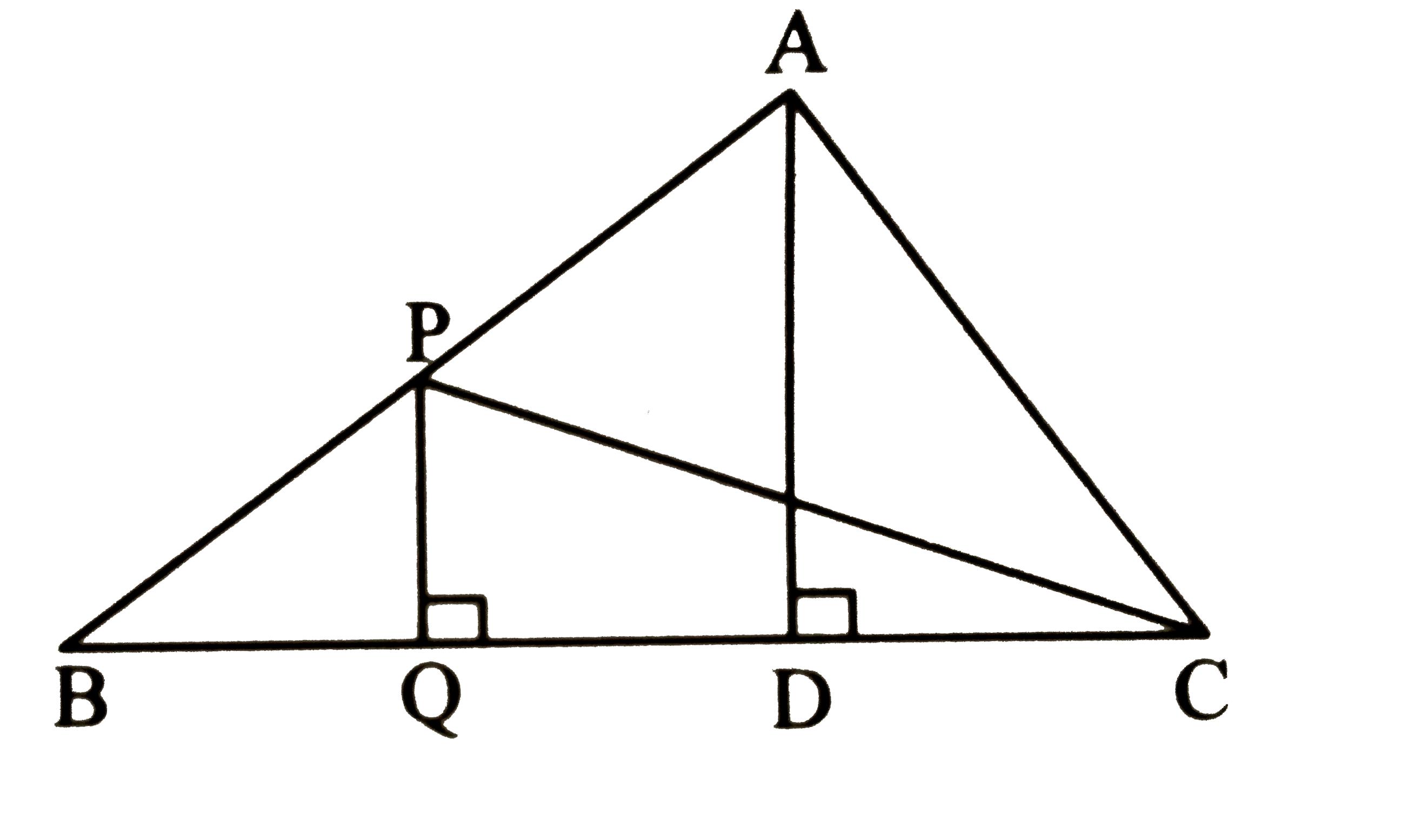
View SolutionIn the adjoining figure, PQ⊥BC,AD⊥BC, then find ratio
A(ΔPBC)A(ΔABC).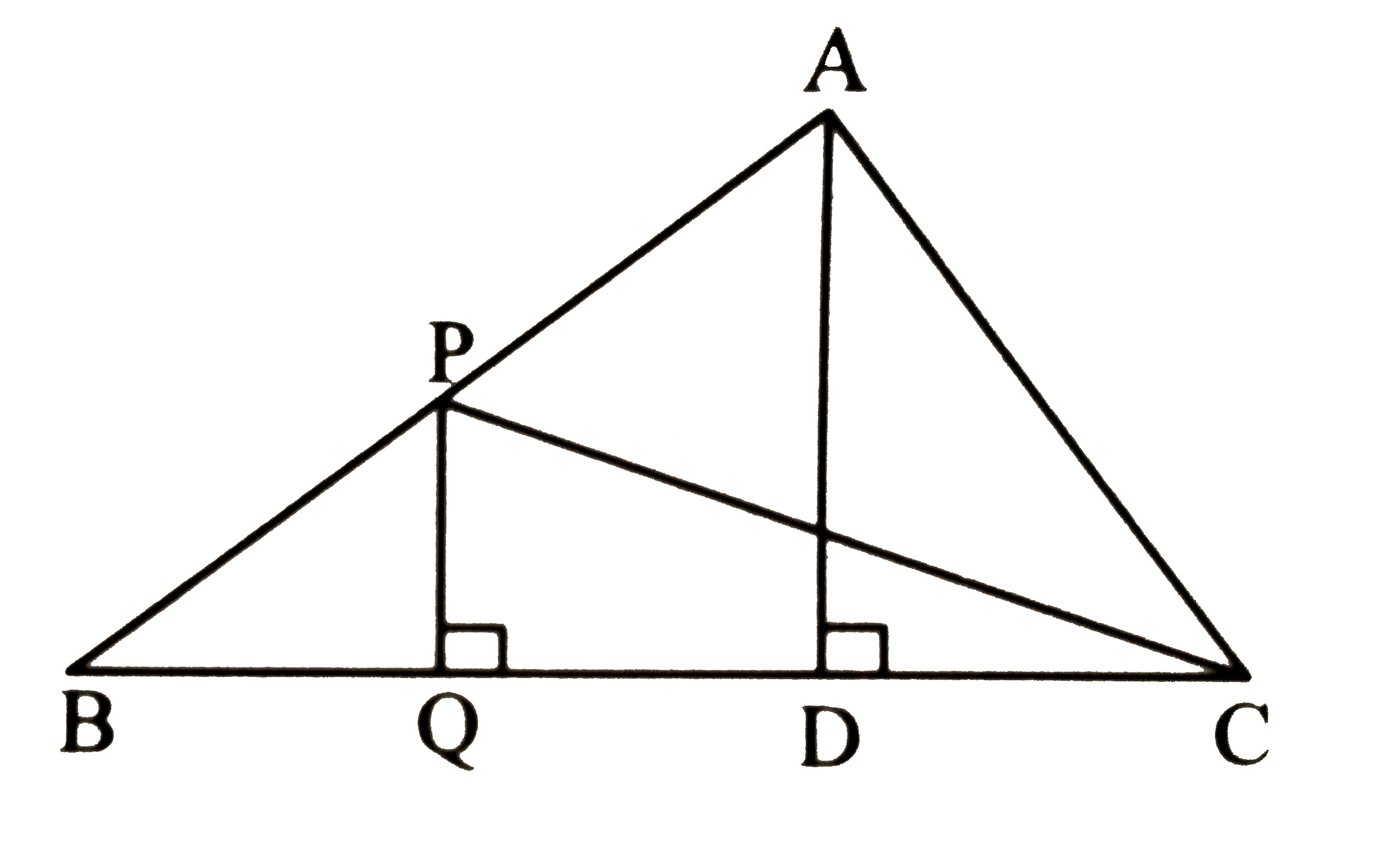
View SolutionIn the adjoining figure, PQ⊥BC,AD⊥BC, then find ratio
A(ΔABC)A(ΔADC).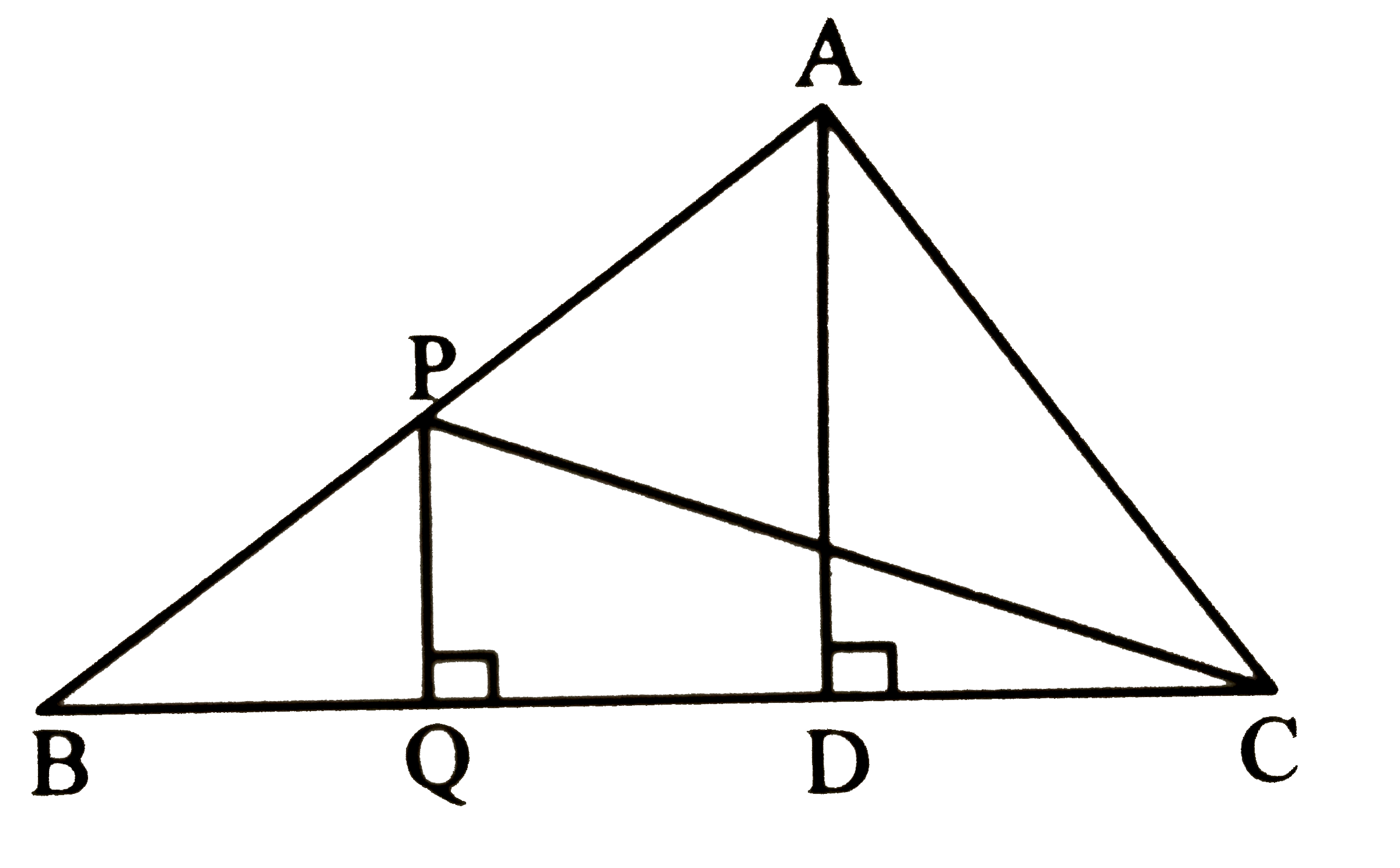
View SolutionIn the given figure, seg AE⊥ seg BC and seg DF ⊥seg BC. Find
i.A(ΔABC)A(ΔDBC)
ii. A(ΔDBF)A(ΔDFC)
iii. A(ΔAEC)A(ΔDBF)
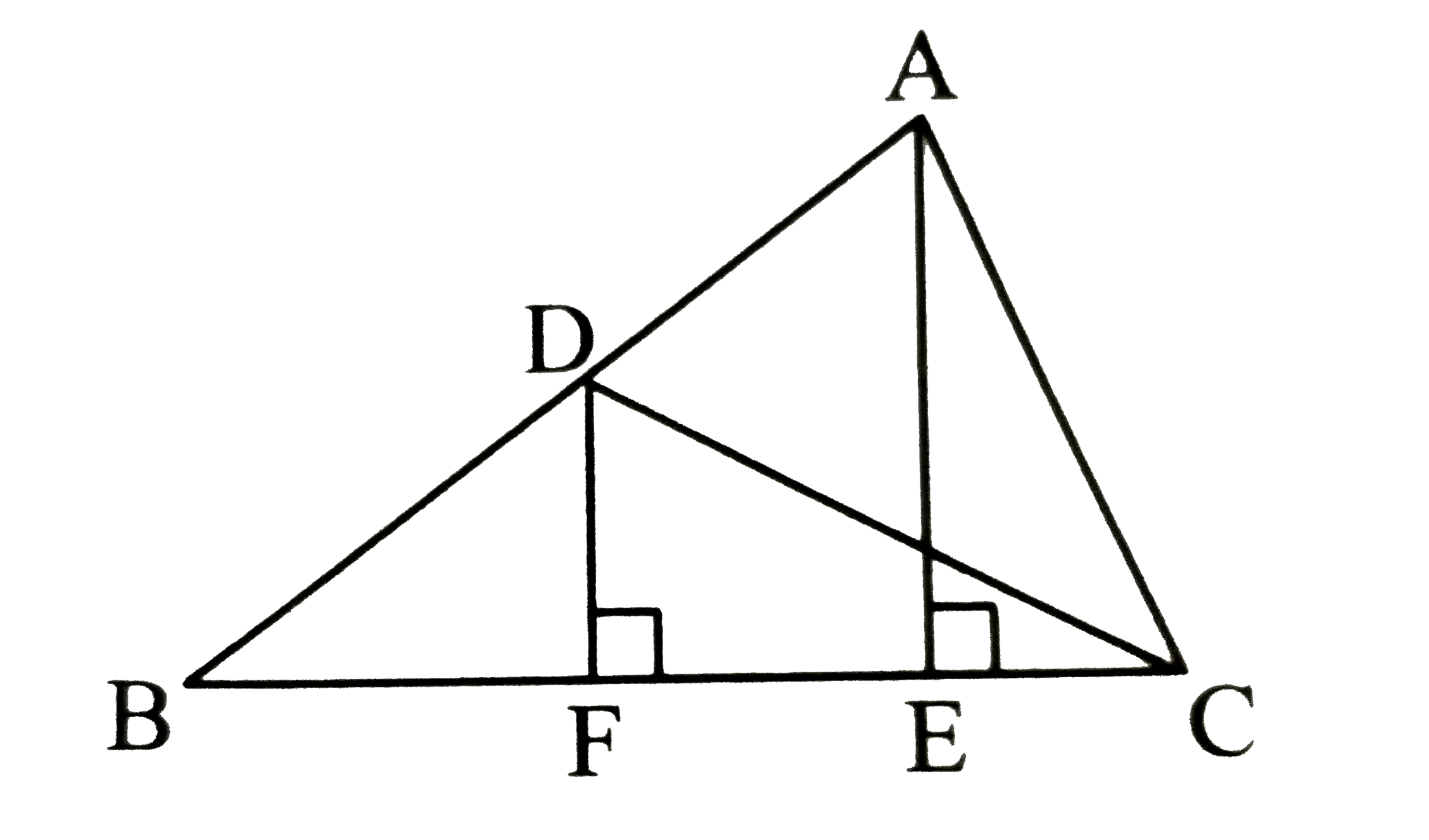
View SolutionIn the following figure AP⊥BC,AD∣∣BC, then find A(ΔABC):A(ΔBCD).
View SolutionIn adjoining figure,AP⊥BC , AD∣∣BC ,then find Ar.(ΔABC):Ar.(ΔBCD)Fig.
View SolutionIn the given figure, in ΔABC, point D is on side AC. If AC = 16, DC = 9 and BP⊥ AC then, find the following rations.
i. A(ΔABD)A(ΔABC)
ii.A(ΔBDC)A(ΔABC)
iii. A(ΔABD)A(ΔBDC)
View Solution