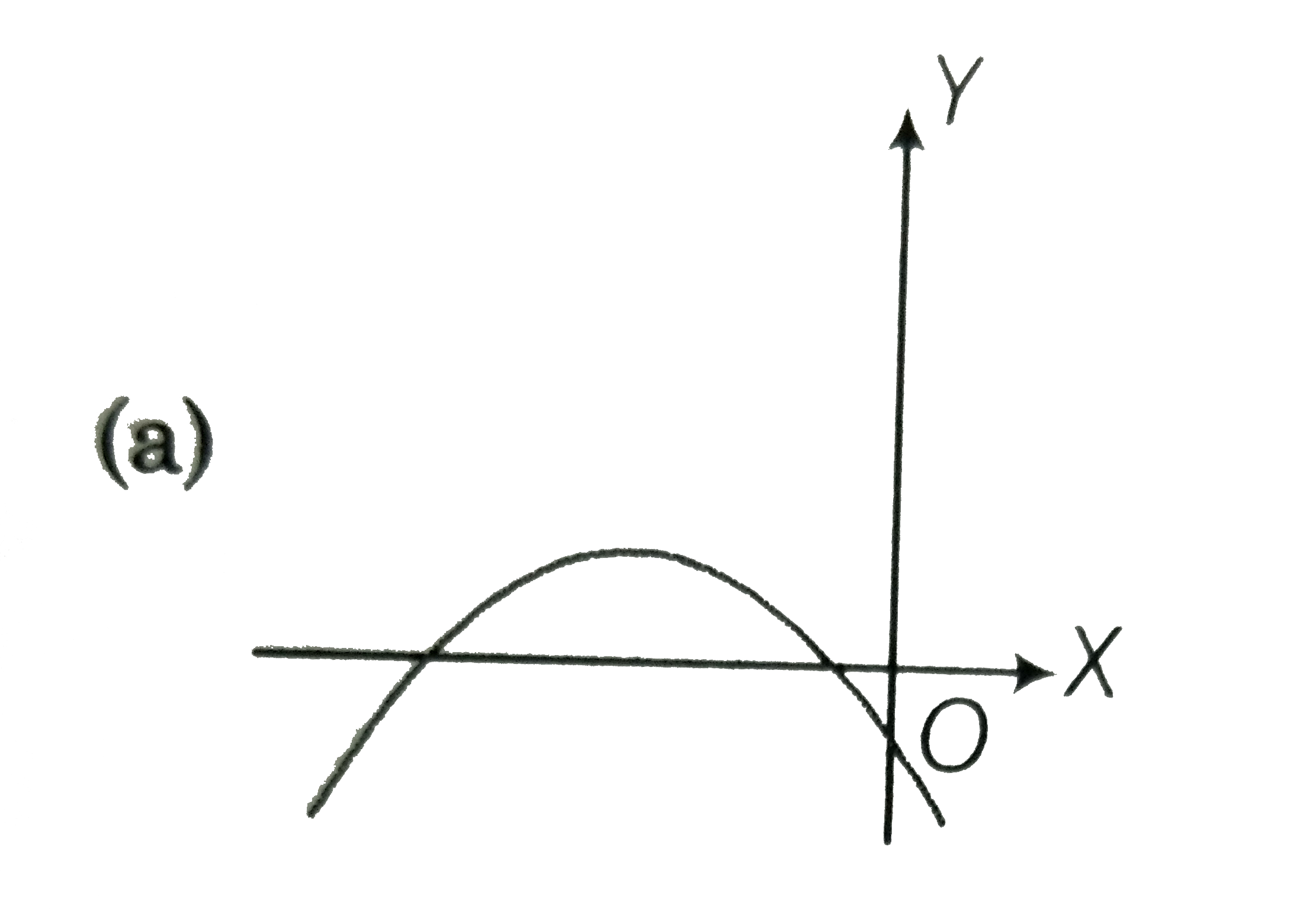
For which of the following graphs of the quadratic expression f(x)=ax2+bx+c, the product of abc is negative
A
B

C
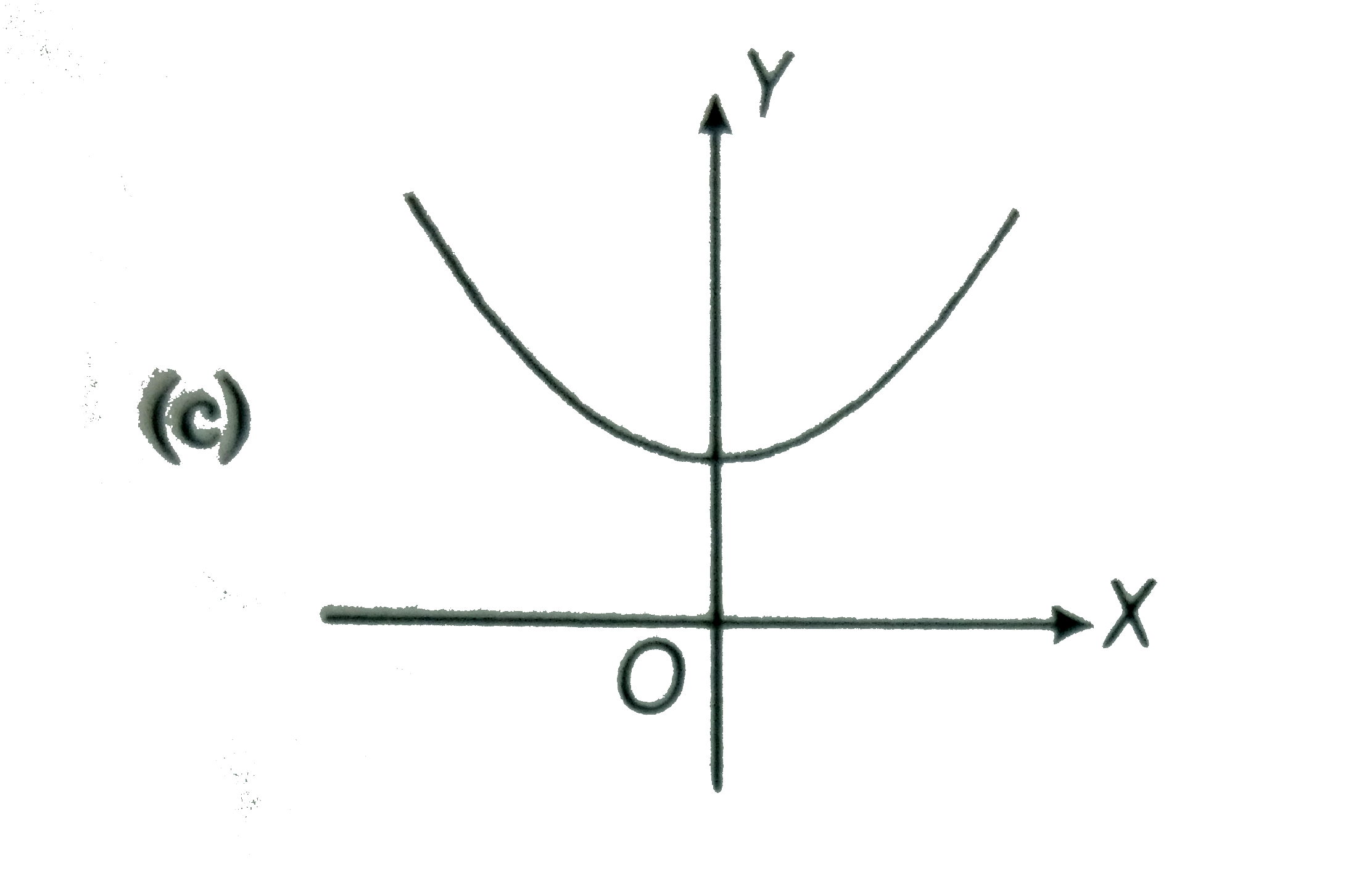
D
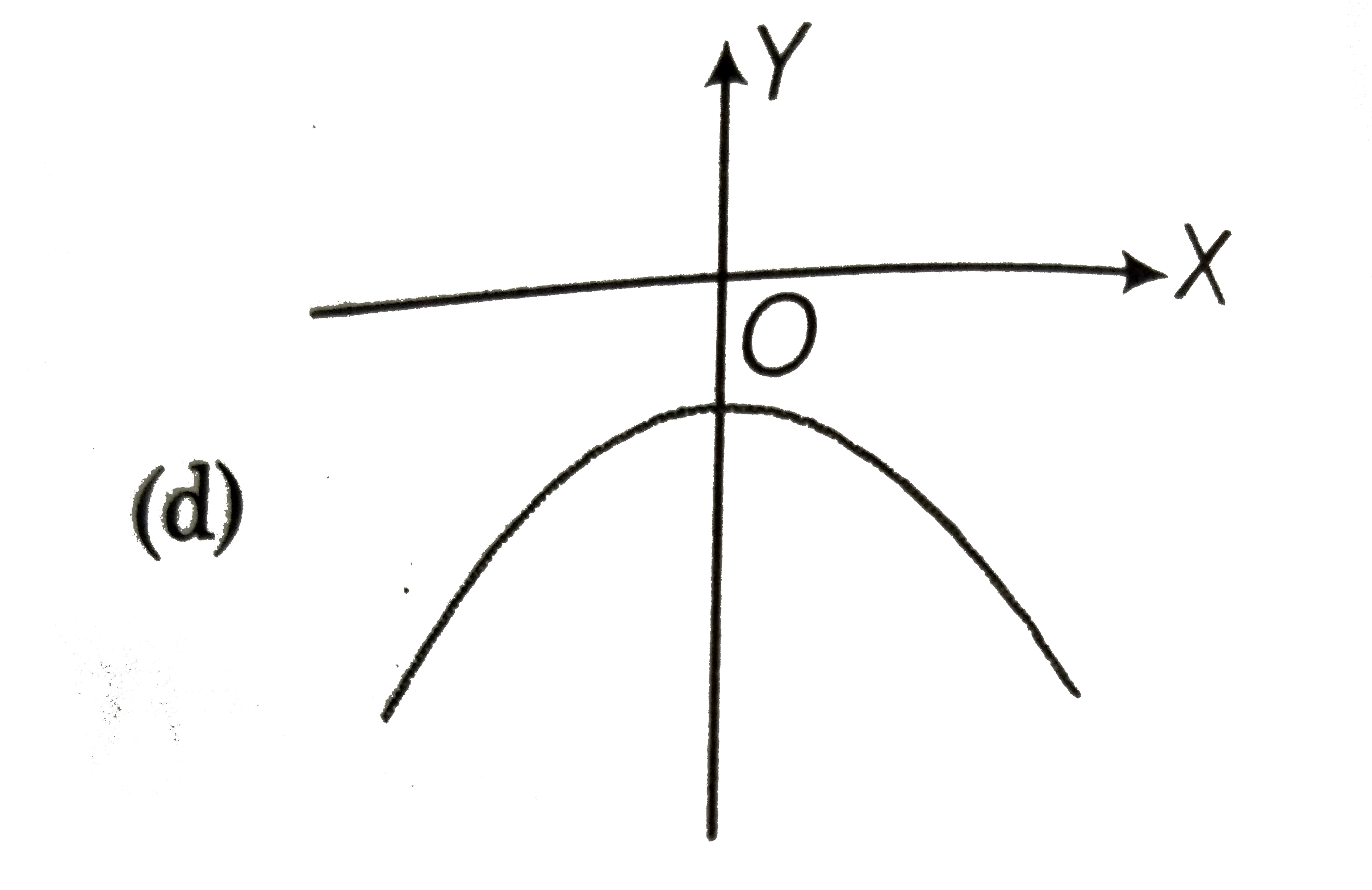
Video Solution
Text Solution
The correct Answer is:A, B, C, D
∵Cut−offY−aξs,putx=0i.e.f(0)=c<br>Option(a)alt0,clt0,-b/(2a)lt0<br>oralt0,clt0,blt0<br>:.abclt0<br>Optionbalt0,cgt0,-b/2agt0<br>oralt0,cgt3,bgt0<br>:.abclt0<br>Optioncagt0, cgt0, -b/(2a)gt0<br>oragt0,cgt0, blt0<br>:.abclt0<br>Option(d)alt0,clt0, -b/(2)lt0<br>oralt0,clt0,blt0<br>:.abclt0
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Passage Based Questions)21videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Single Integer Answer Type Questions)10videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - SCQ_TYPE1videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)44videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One or More
For which of the following graphs of the quadratic expression y=ax2+bx+c, the product a.b.c is negative.
A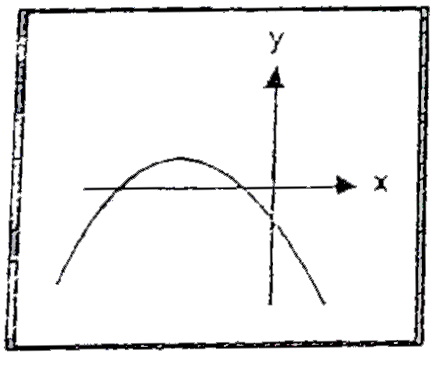 B
B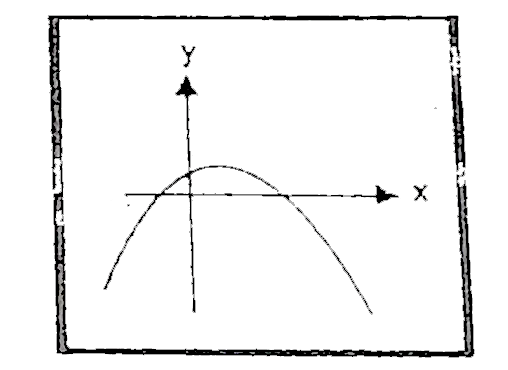 C
C D
D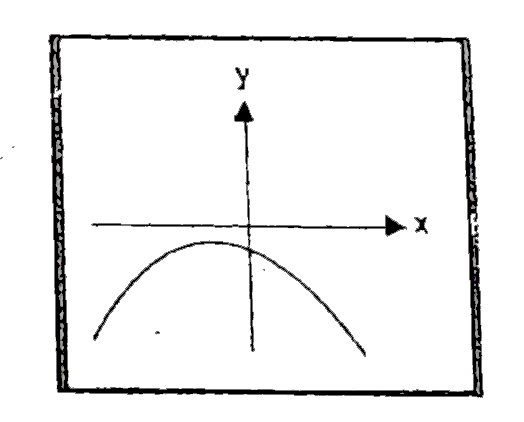
- Question 2 - Select One
For which of the following graphs the quadratic expression y=ax2+bx+c the product abc is negative ?
A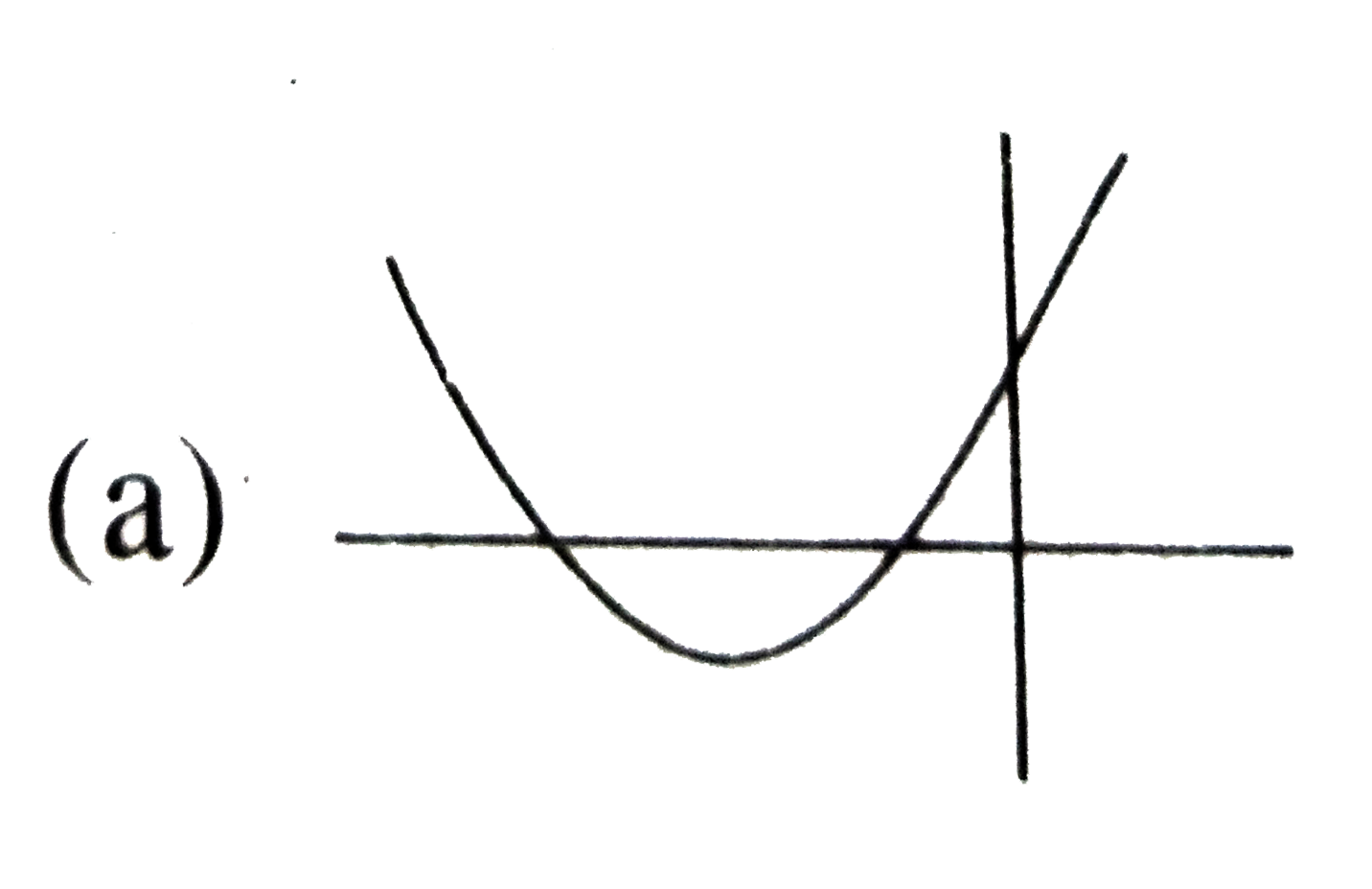 B
B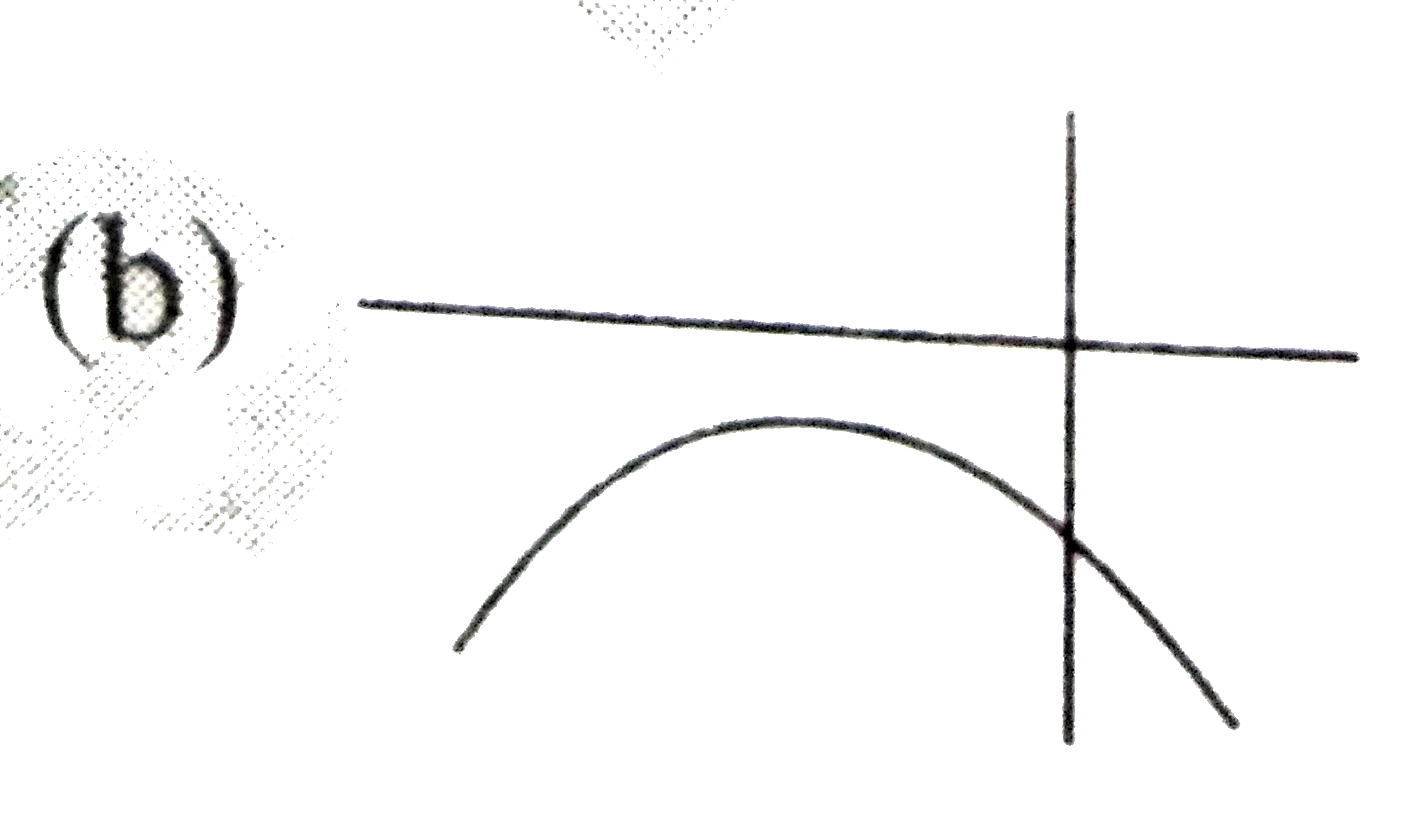 C
C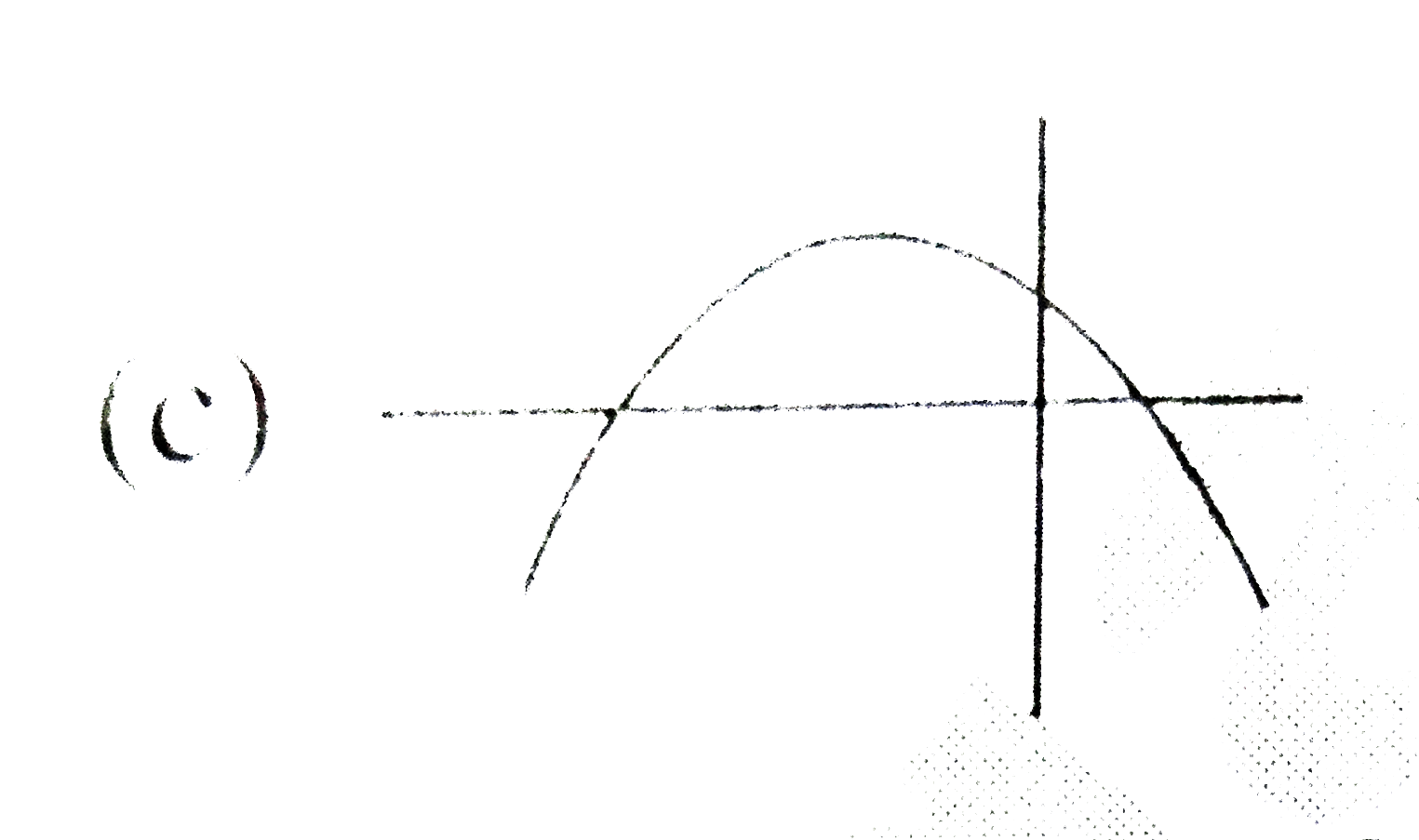 D
D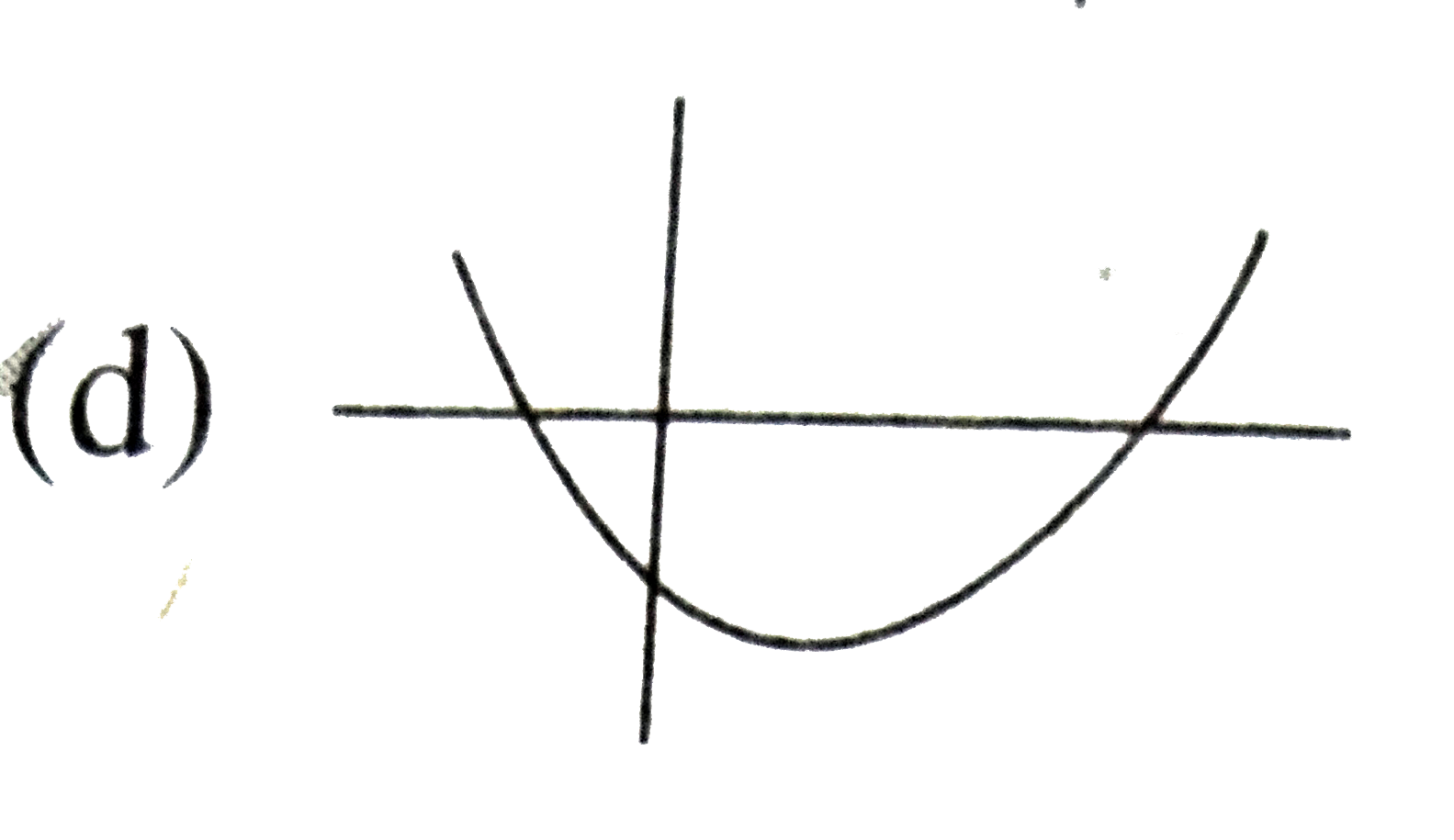
- Question 3 - Select One or More
If a,b,c ∈R, then for which of the following graphs of the quadratic polynomial y=ax2−2bx+c(a≠0), the product (abc) is negative ?
A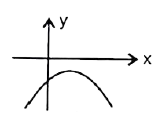 B
B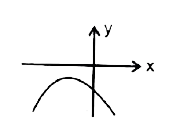 C
C D
D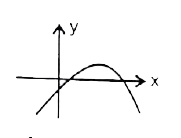
The quadratic expression ax2+bx+c>0 ∀x∈R ,then
View Solutionwhich of the following graph represents the expression f(x)=ax2+bx+c (a≠0) when a>0,b<0 $ c<0 ?
View SolutionIf the quadratic polynomial is ax2+bx+c , then product of zeroes is ……… .
View SolutionThe graph of quadratic polynomical f(x)=ax2+bx+c is shown below
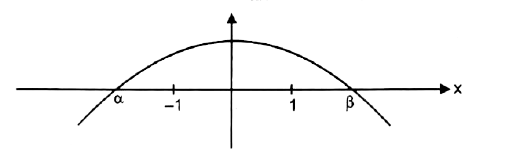 View Solution
View SolutionThe quadratic expression ax2+bx+c>0∀x∈R, then :
View Solution

