The adjoining graph of y=ax2+bx+c shows that
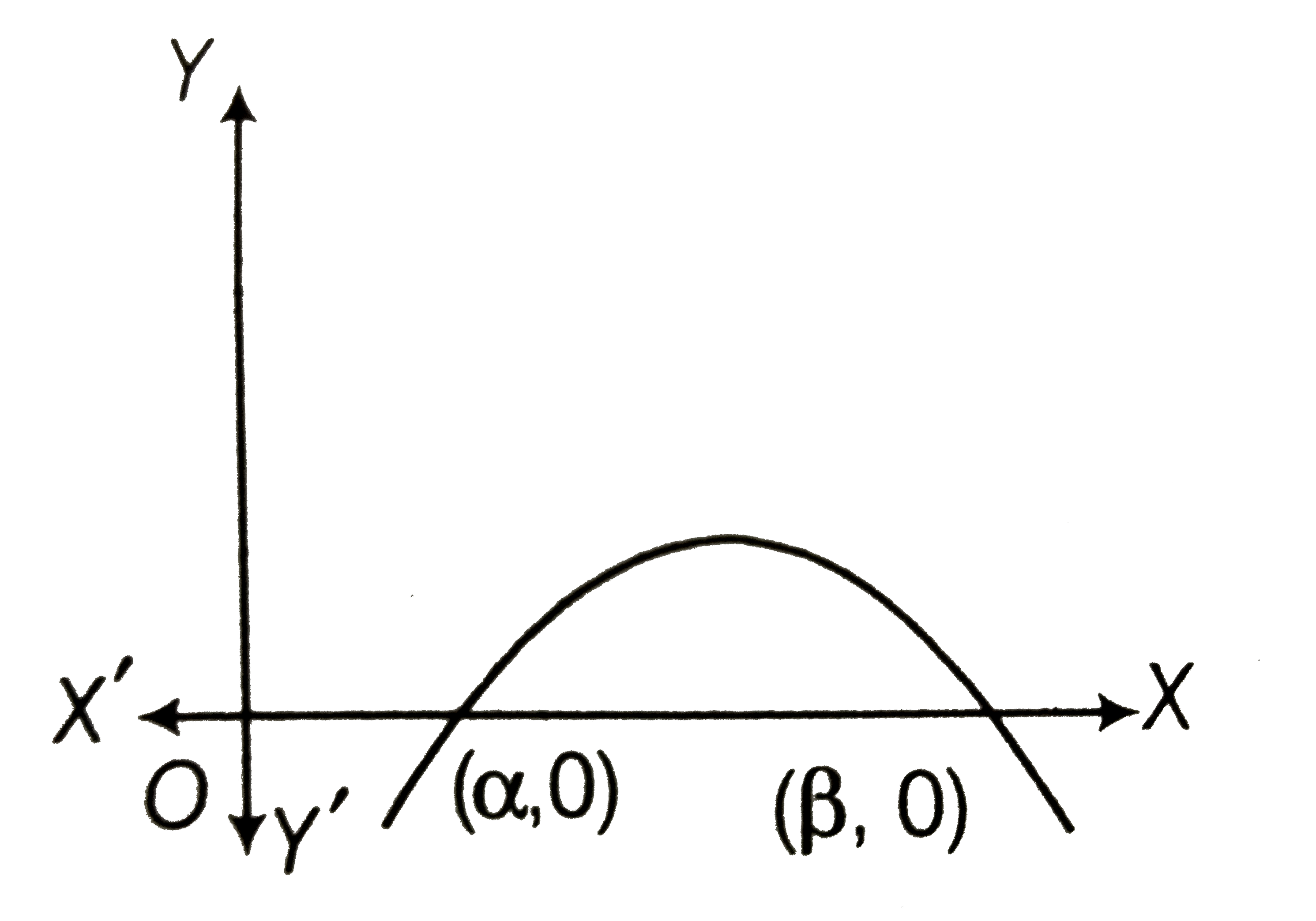
A
a<0
B
b2<4ac
C
c>0
D
a and b are of opposite signs
Video Solution
Text Solution
The correct Answer is:A, D
It is clear from graph that the equation y=ax2+bx+c=0 has two real and distinct roots. Therefore
b2−4ac>0………..i
∴ Parabola open downwards.
a<0
and y=ax2+bx+c cuts off Y axis at x=0
∴y=c<0
⇒c<0
and x-coordinate of vertex >0
⇒−b2a>0⇒ba<0
⇒b>0[∵a<0]
It is clear that a and b are of opposite signs.
|
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Passage Based Questions)
21 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Single Integer Answer Type Questions)
10 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - SCQ_TYPE
1 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
44 Videos
Similar Questions
Knowledge Check
Shows graph of y=ax2+bx+c . Then which one of the following is not true.
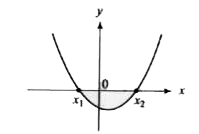 Aa>0Bc<0Cb2−4ac>0Db>0
Aa>0Bc<0Cb2−4ac>0Db>0
For following graphs of y=ax2+bx+cwith a,b,c c R, comment on the sign of
View Solution(ax2+bx+c)6
View SolutionThe diagram shows the grap of y=ax2+bx+c. Then
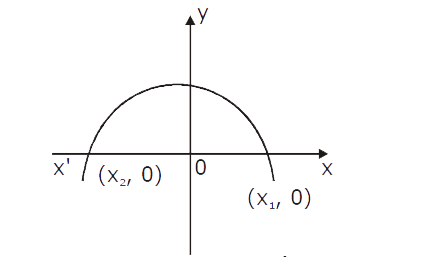
View SolutionIf graph of y=ax2+bx+c is as shown,then which of the following is correct? (where D equals b2−4ac)
View SolutionIf a>0andb2−4ac=0, then the graph of y=ax2+bx+c touches x-axis and lies above x-axis.
View SolutionFocus of parabola y=ax2+bx+c is
View SolutionThe following figure shows the graph of f(x)=ax2+bx+c, find the sign of a,bandc.
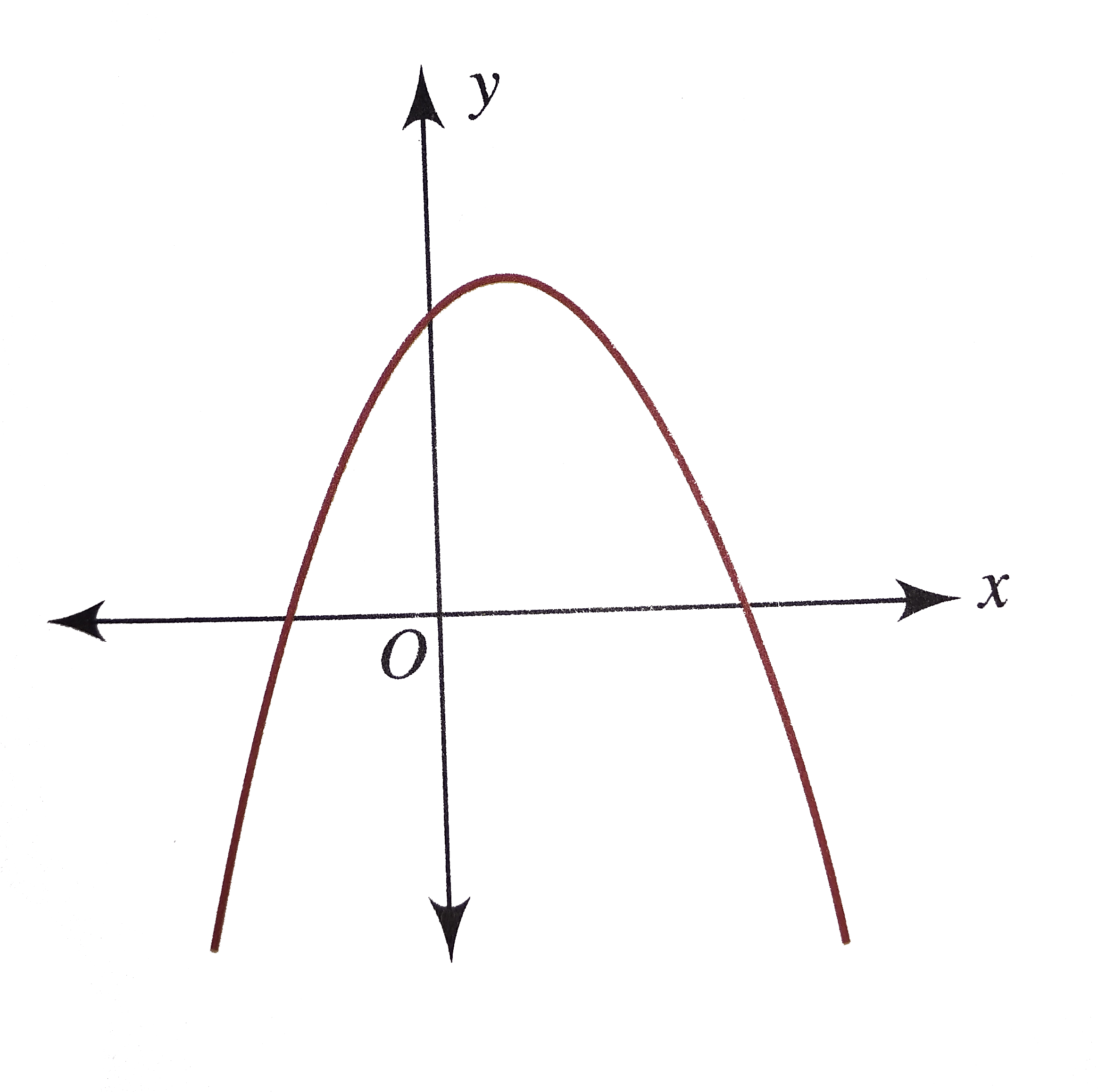
View Solution
