ax2+bx+c=0(a>0), has two roots αandβ such α<−2andβ>2, then
A
4a−2|b|+c<0
B
9a−3|b|+c<0
C
a−|b|+c<0
D
c<0,b2−4ac>0
Video Solution
Text Solution
The correct Answer is:A, C, D
Here D>0
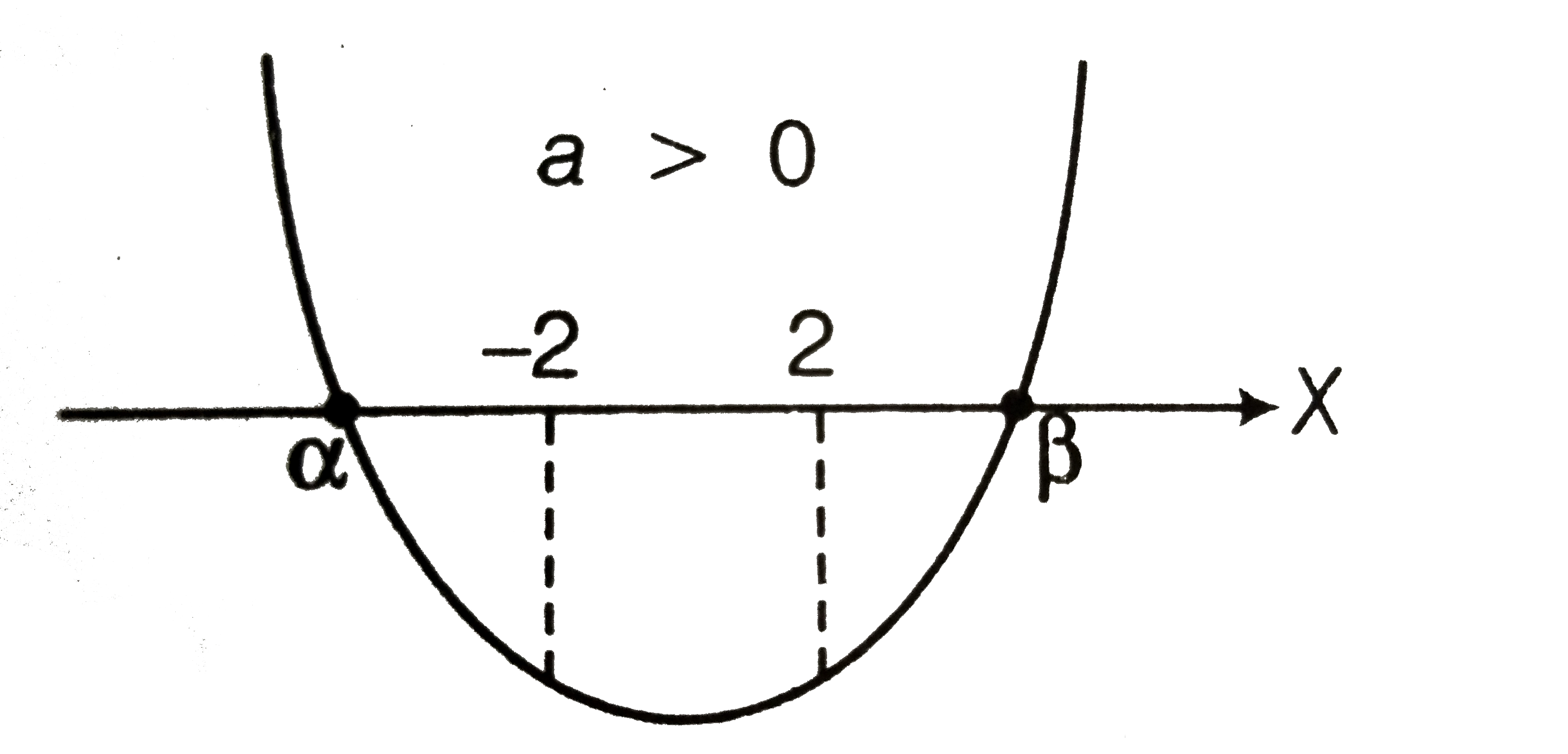
b2−4ac>0
or b2>4ac…… i and f(0)<0
⇒c<0..ii
f(1)<0
⇒a+b+c<0………iii
f(−1)<0
⇒a−b+c<0………..iv
f(2)<0
⇒4a+2b+c<0………v
f(−2)<0
⇒4a−2b+c<0...............vi
From Eqs i and ii we get
c<0,b2−4ac>0
From Eqs. (iii) and (iv) we get
a−|b|+c<0
and from Eqs (v) and (vi) we get
4a−2|b|+c<0
|
Topper's Solved these Questions
- THEORY OF EQUATIONSBook:ARIHANT MATHSChapter:THEORY OF EQUATIONSExercise:Exercise (Passage Based Questions)
Explore 21 Videos
- THEORY OF EQUATIONSBook:ARIHANT MATHSChapter:THEORY OF EQUATIONSExercise:Exercise (Single Integer Answer Type Questions)
Explore 10 Videos
- THEORY OF EQUATIONSBook:ARIHANT MATHSChapter:THEORY OF EQUATIONSExercise:SCQ_TYPE
Explore 1 Video
- THE STRAIGHT LINESBook:ARIHANT MATHSChapter:THE STRAIGHT LINESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 18 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBook:ARIHANT MATHSChapter:THREE DIMENSIONAL COORDINATE SYSTEMExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 44 Videos
Similar Questions
Knowledge Check
If the equation ax2+bx+c=0(a>0) has two roots αandβ such that α<−2andβ>2, then
Ab2−4ac>0B4a+2|b|+c<0Ca+|b|+c<0Dc<0If the equation ax2+bx+c=0(a<0) has two roots α and β such that α<−3 and β>3, then
A4a−2|b|+c<0B9a−3|b|+c<0Ca−|b|+c<0Dc<0,b2−4ac>0If α and β are the roots of the equation ax2+bx+c=0, and px2+qx+r=0 has roots 1−αα and 1−ββ, then r is equal to
Aa+2bBa+b+cCab+bc+caDabc
If αandβ be the roots of the equation ax2+bx+c=0 then equation whose roots are α+βandαβ is
View SolutionIf α,β are roots of the equation ax2+bx+c=0 then the equation whose roots are 2α+3β and 3α+2β is
View SolutionIf a,b,c are in A.P and ax2+bx+c=0 has integral roots α,β, then α+β+αβ can be equal to
(A) -1 (B) 0 (C) 7 (D) -7
View SolutionIf αandβ are the roots the equations ax2+bx+c=0, where a≠0 then (aα+b)(aβ+b) is equal to :
View SolutionIf α,β are the roots of ax2+bx+c=0, then find the quadratic equation whose roots are α+β,αβ.
View Solution