For which of the following graphs of the quadratic expression y=ax2+bx+c, the product a.b.c is negative.
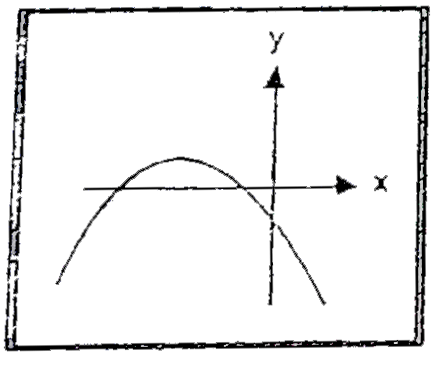
A
B
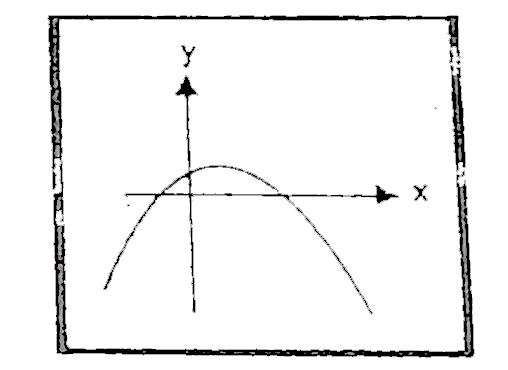
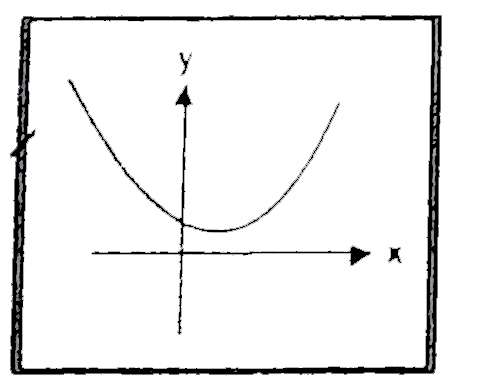
C
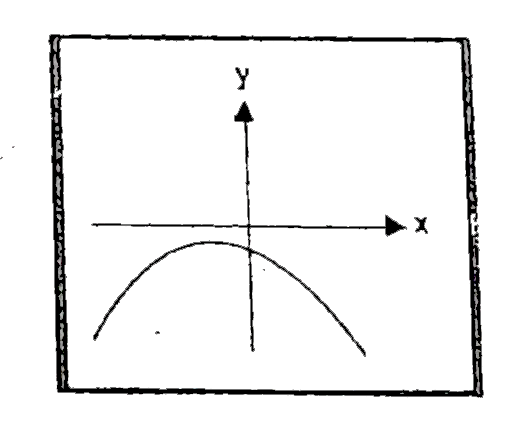
D
Video Solution
Text Solution
The correct Answer is:A, B, C, D
(A). −b2a≤0
⇒−b≥0[∵a≤0]
a≤0,c≤0,b≤0
(B). 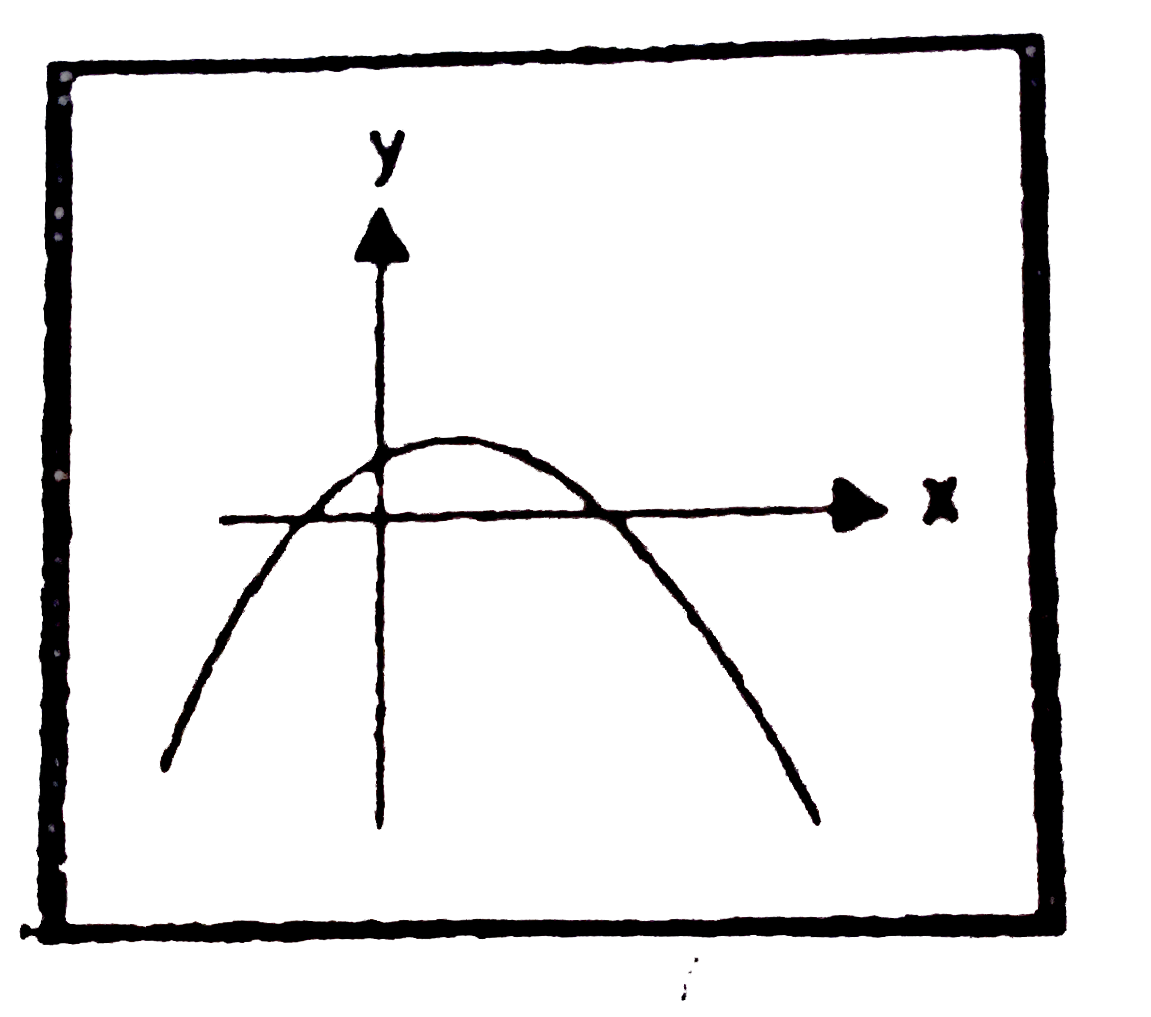
−b2a≥0⇒−b≤0⇒b≥0
a≤0,c≤0,b≤0
∵abc≤0
(C). 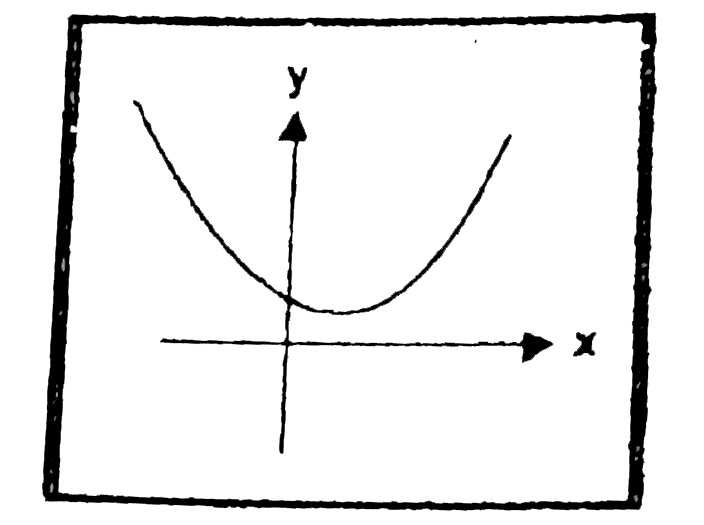
−b2a≥0⇒−b≥0⇒b≤0
a≥0,c≥0,b≤
∵abc≤0
(D). 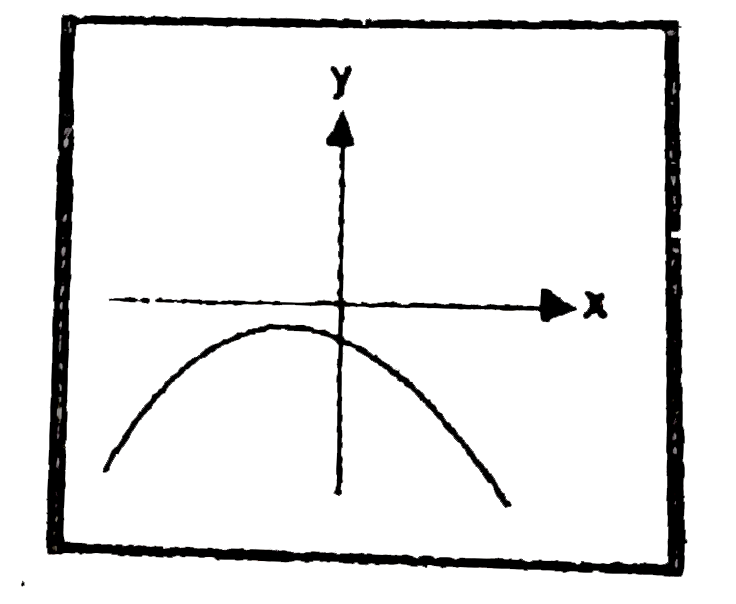
a≤0,c≤0,b≤0
∵≤0
|
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:MATHEMATICS
Explore 263 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - I MATHMATICS
Explore 84 Videos
- TEST PAPERBook:RESONANCEChapter:TEST PAPERExercise:CHEMISTRY
Explore 37 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:MATHEMATICS
Explore 131 Videos
Similar Questions
Knowledge Check
For which of the following graphs of the quadratic expression f(x)=ax2+bx+c, the product of abc is negative
A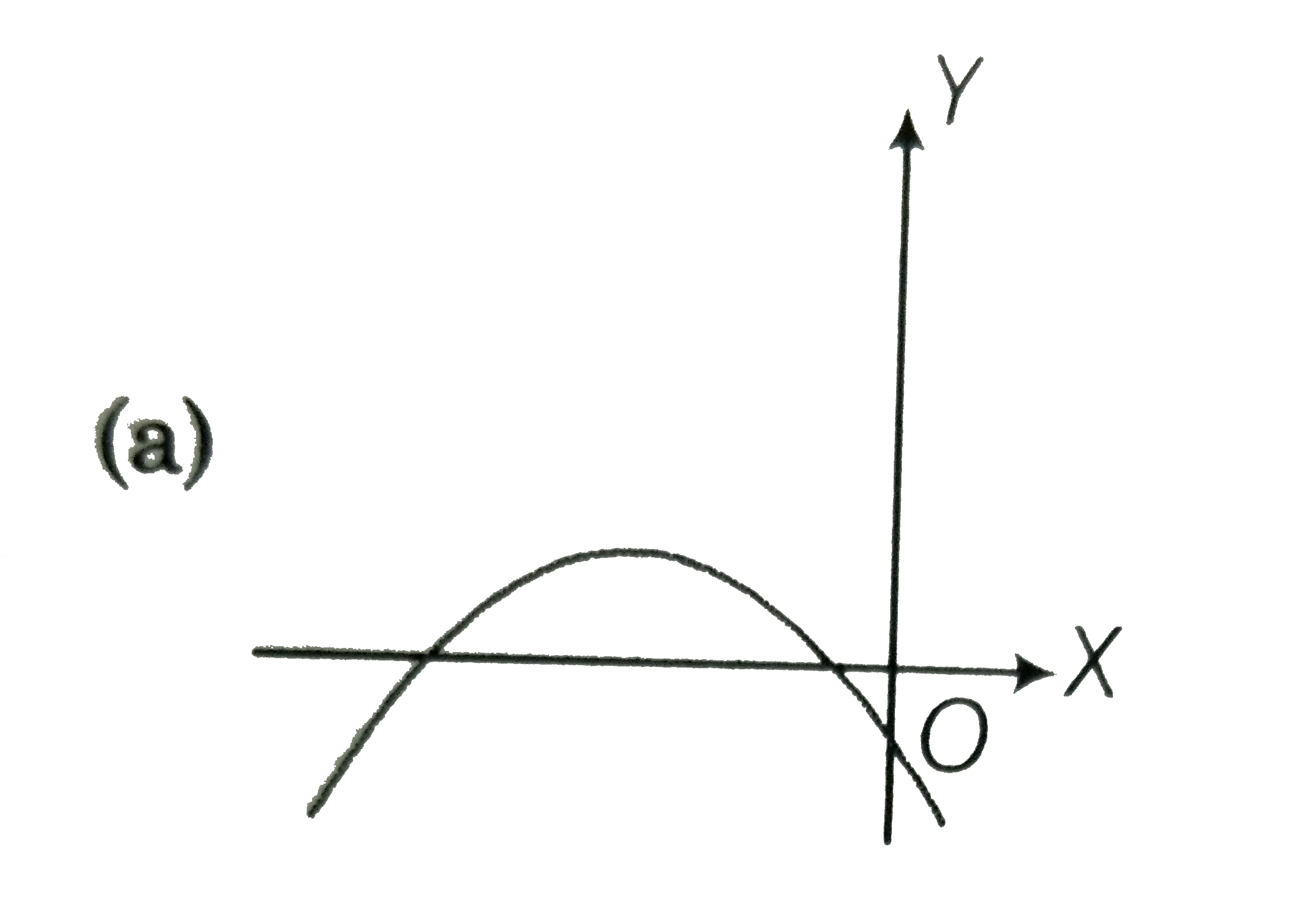 B
B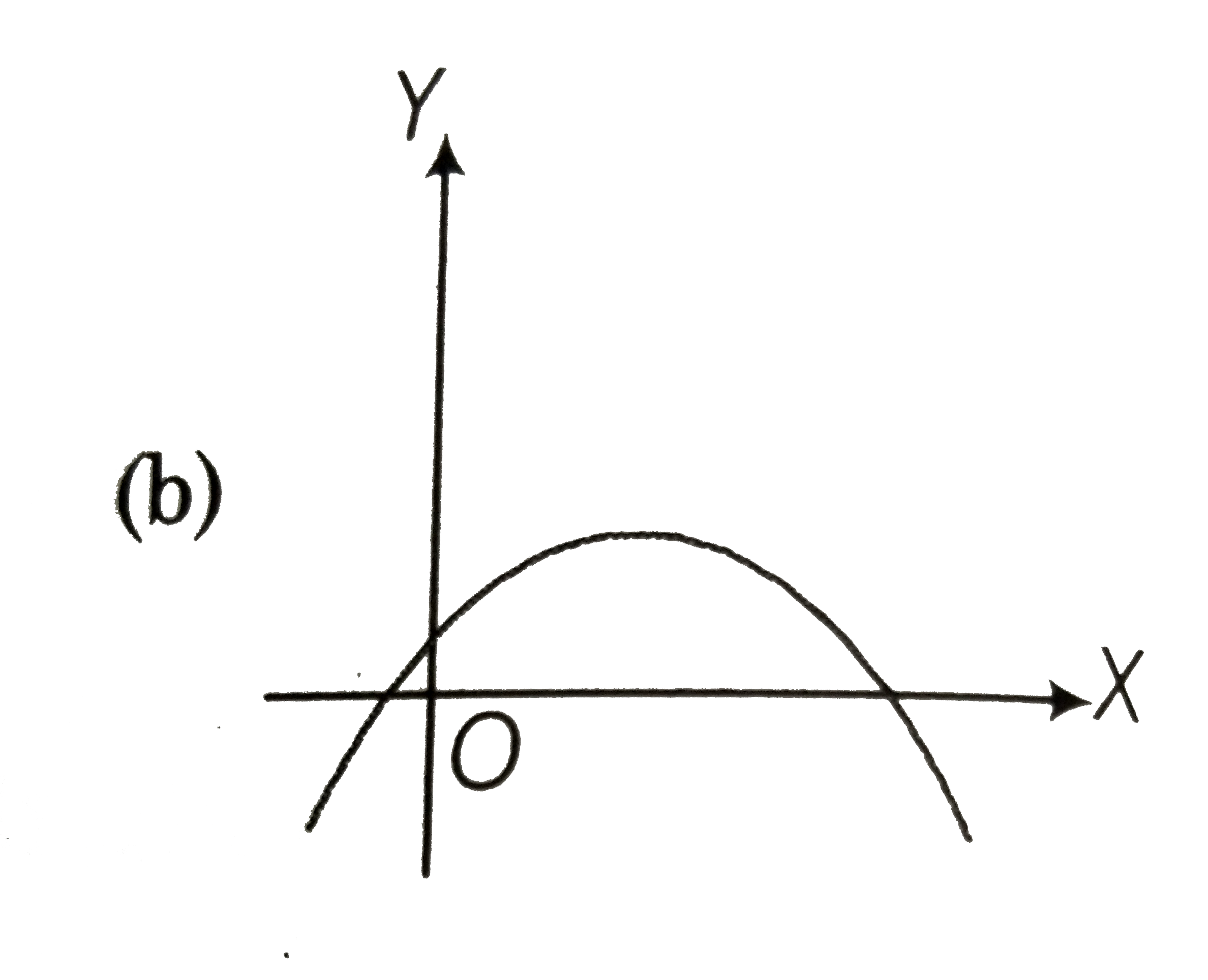 C
C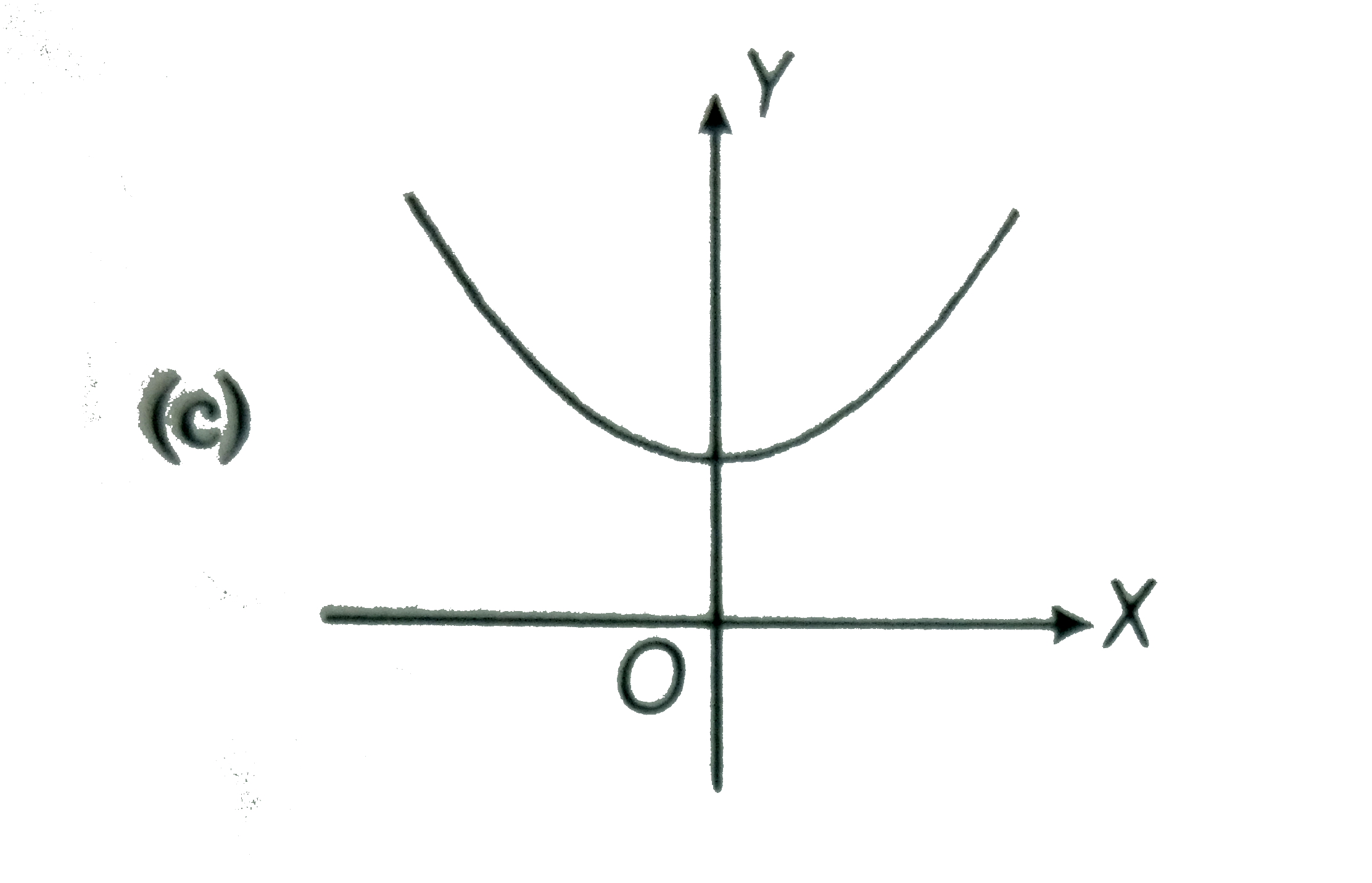 D
D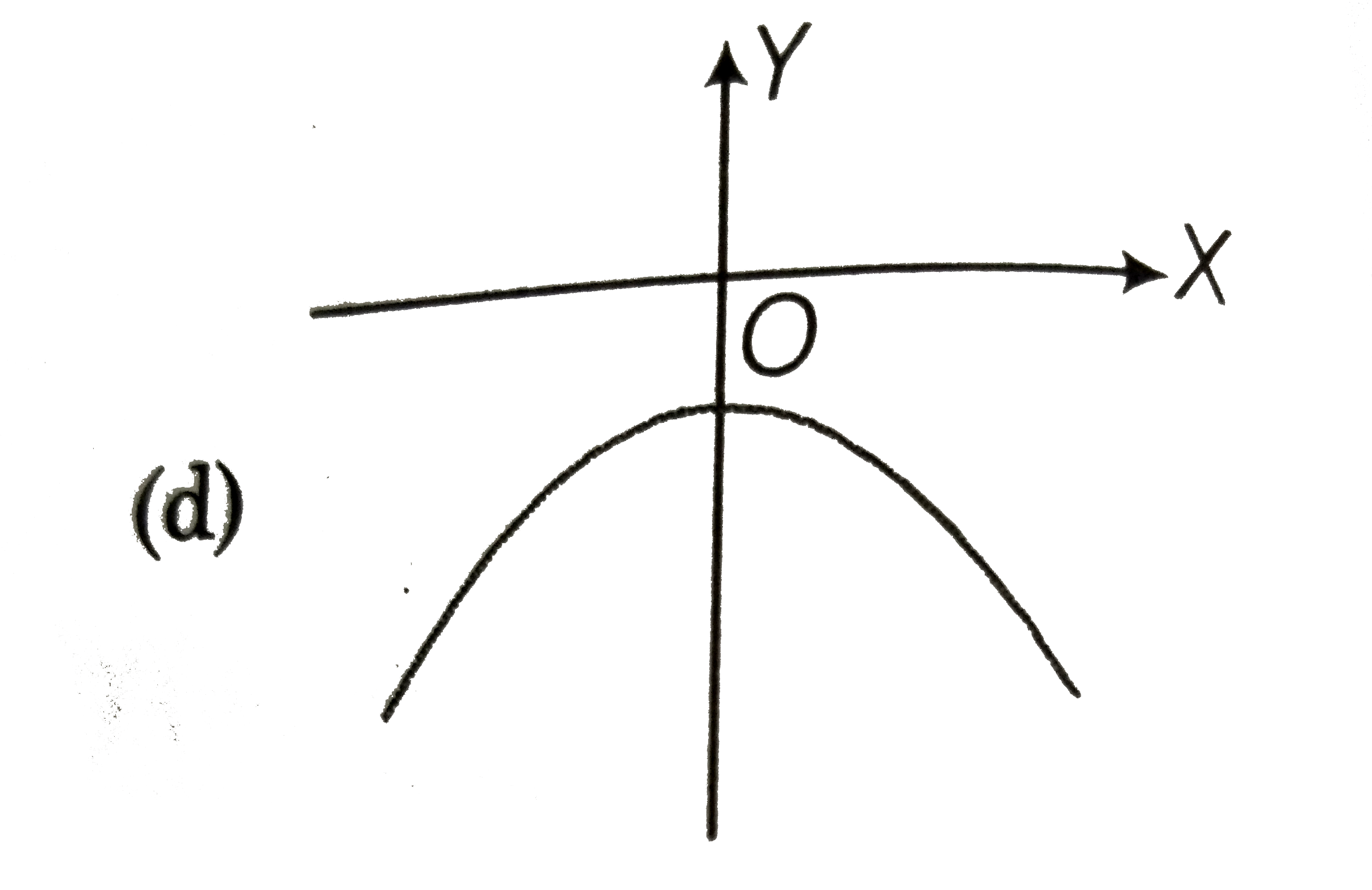
For which of the following graphs the quadratic expression y=ax2+bx+c the product abc is negative ?
A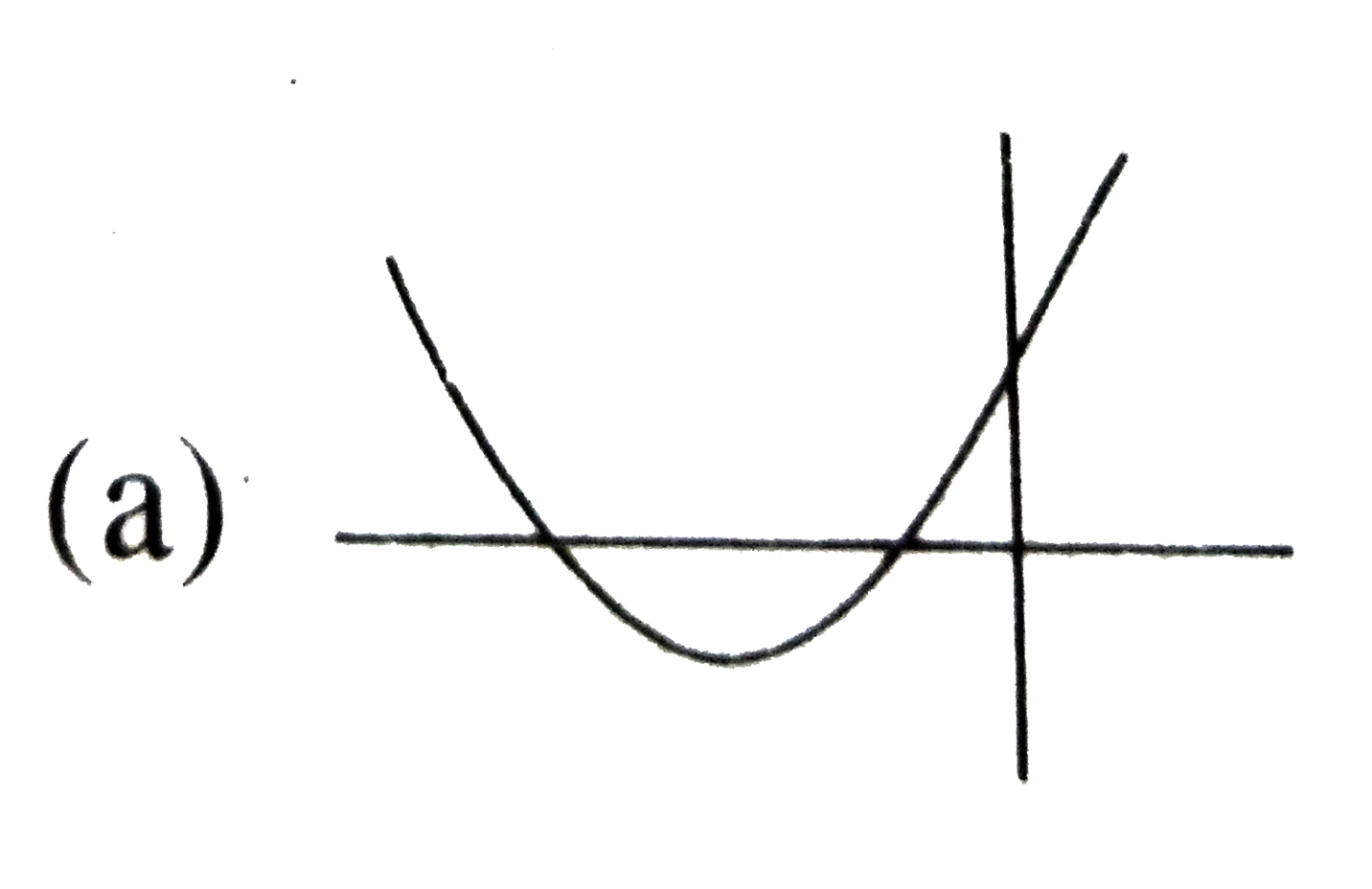 B
B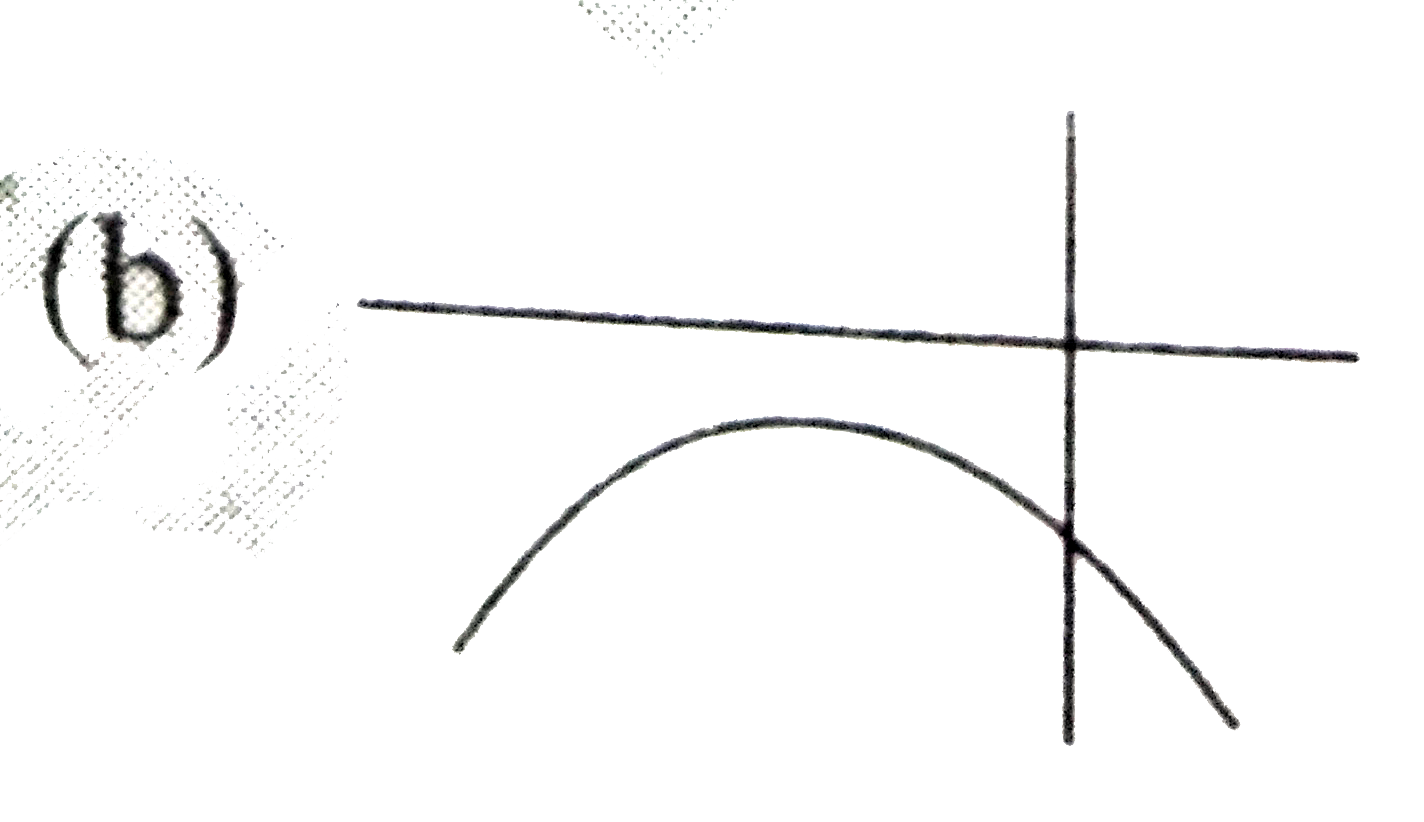 C
C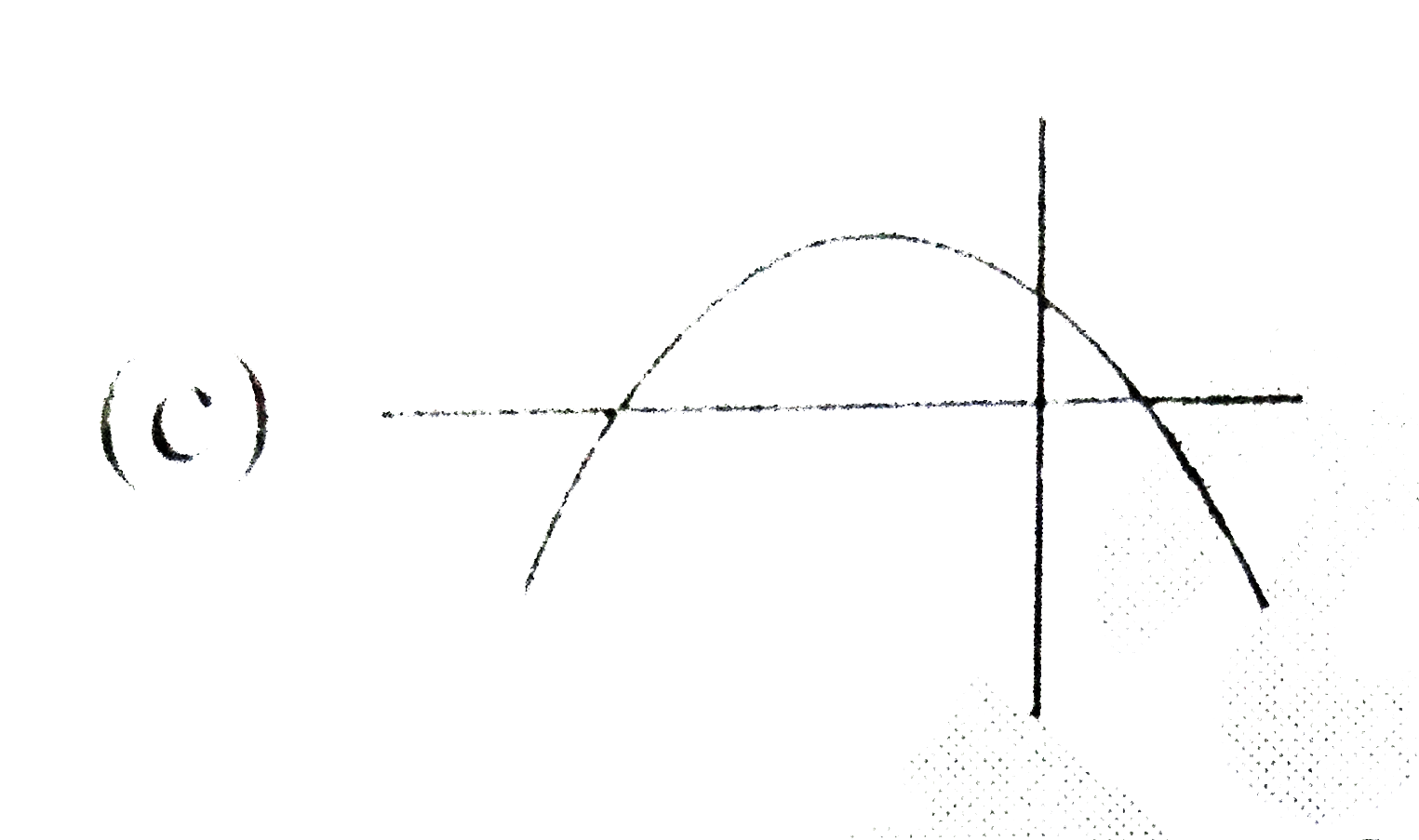 D
D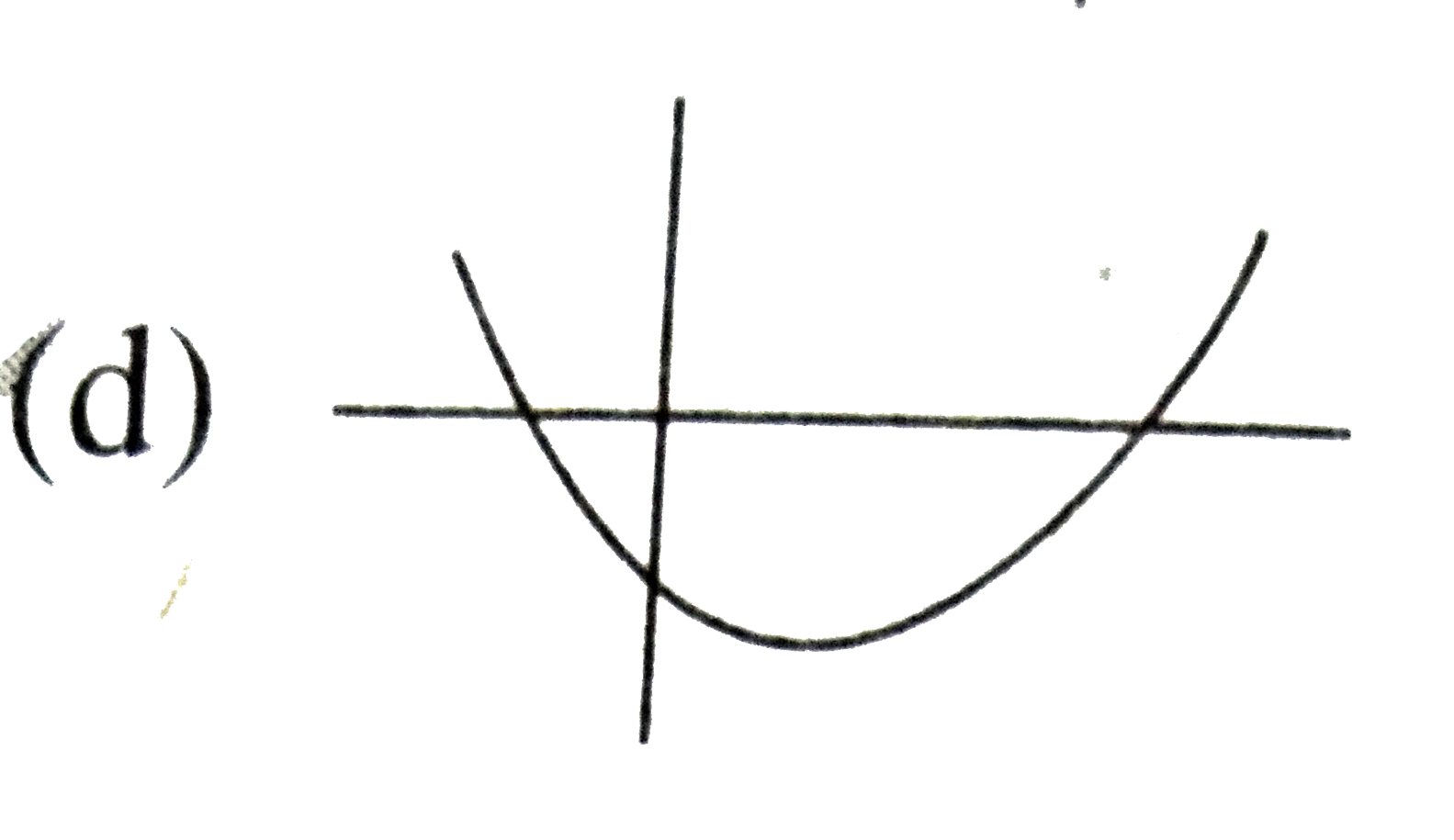
If a,b,c ∈R, then for which of the following graphs of the quadratic polynomial y=ax2−2bx+c(a≠0), the product (abc) is negative ?
A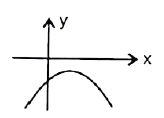 B
B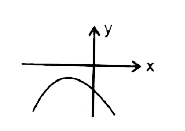 C
C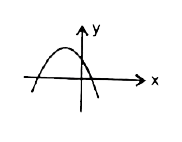 D
D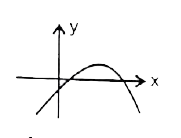
Please explain Range of quadratic expression f(x)=ax2+bx+c
View Solutionwhich of the following graph represents the expression f(x)=ax2+bx+c (a≠0) when a>0,b<0 $ c<0 ?
View SolutionIf the quadratic polynomial is ax2+bx+c , then product of zeroes is ……… .
View SolutionThe quadratic expression ax2+bx+c>0∀x∈R, then :
View SolutionThe quadratic equation ax2+bx+c=0 has real roots if:
View Solution

