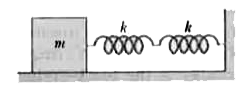
Two spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

12π√kM
12π√k2M
12π√2kM
12π√MK
The correct Answer is:B
The spring constant of spring connected in series is equal to
k=k1k2(k1+k2)−k2
Thus frequency of oscillation of given system is
f=12π√k2m
Topper's Solved these Questions
Similar Questions
In Fig. 15.29 two springs are joined and connected to a block of mass 0.490kg that is set oscillating over a frictionless floor. The springs each have spring constant k= 5000N/m. What is the frequency of the oscillations?
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View Solution
Knowledge Check
Two springs are joined and connected to mass m as shown. If the springs separately have force constants K1 and K2 , then frequency of oscillation of mass m is
 A12π√K1K2(K1+K2)mB2π√(K1+K2)mK1K2C2π√K1K2mD12π√mK1+K2
A12π√K1K2(K1+K2)mB2π√(K1+K2)mK1K2C2π√K1K2mD12π√mK1+K2A block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
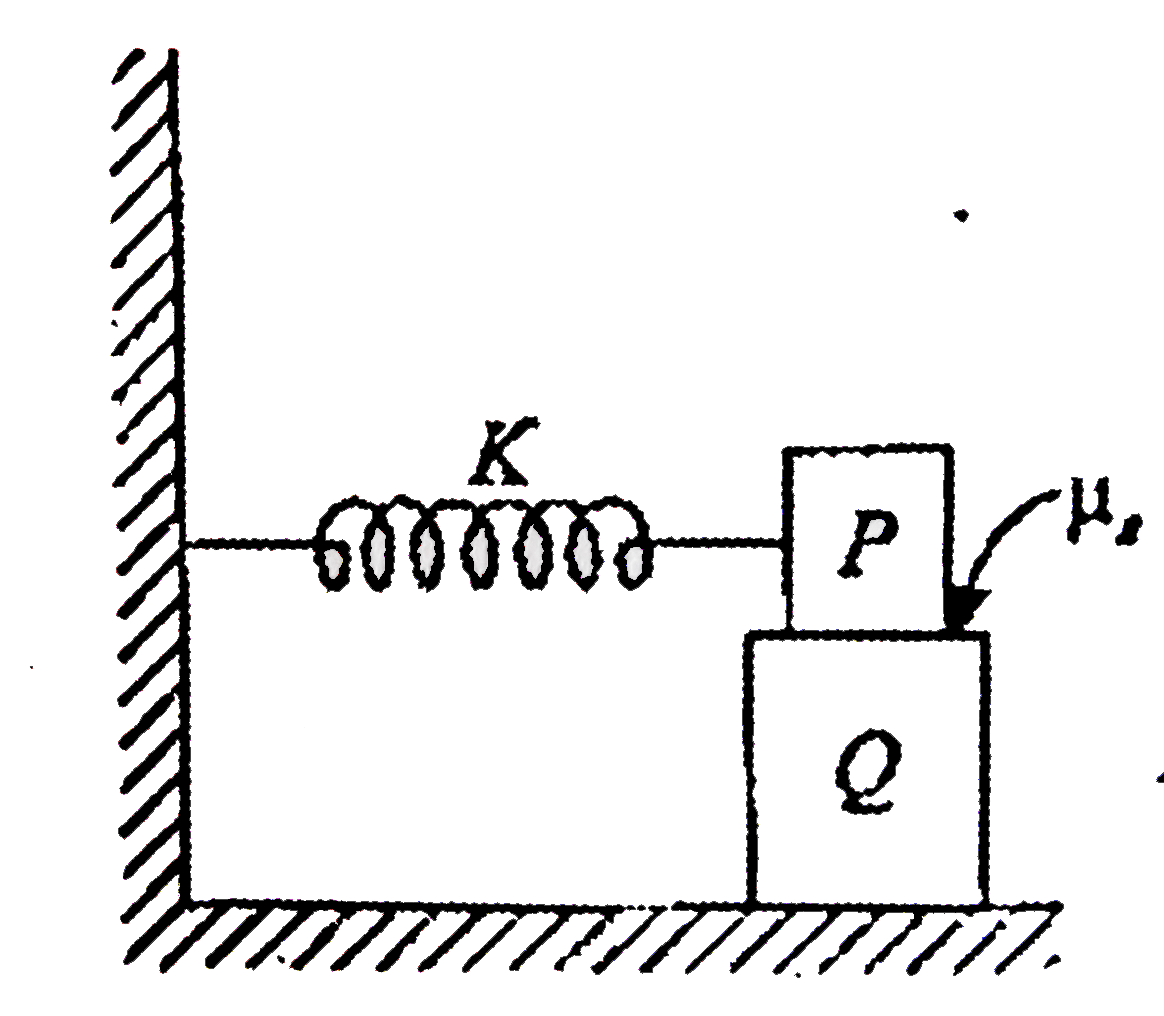 A13KA2B23KA2C12KA2D14KA2
A13KA2B23KA2C12KA2D14KA2A block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
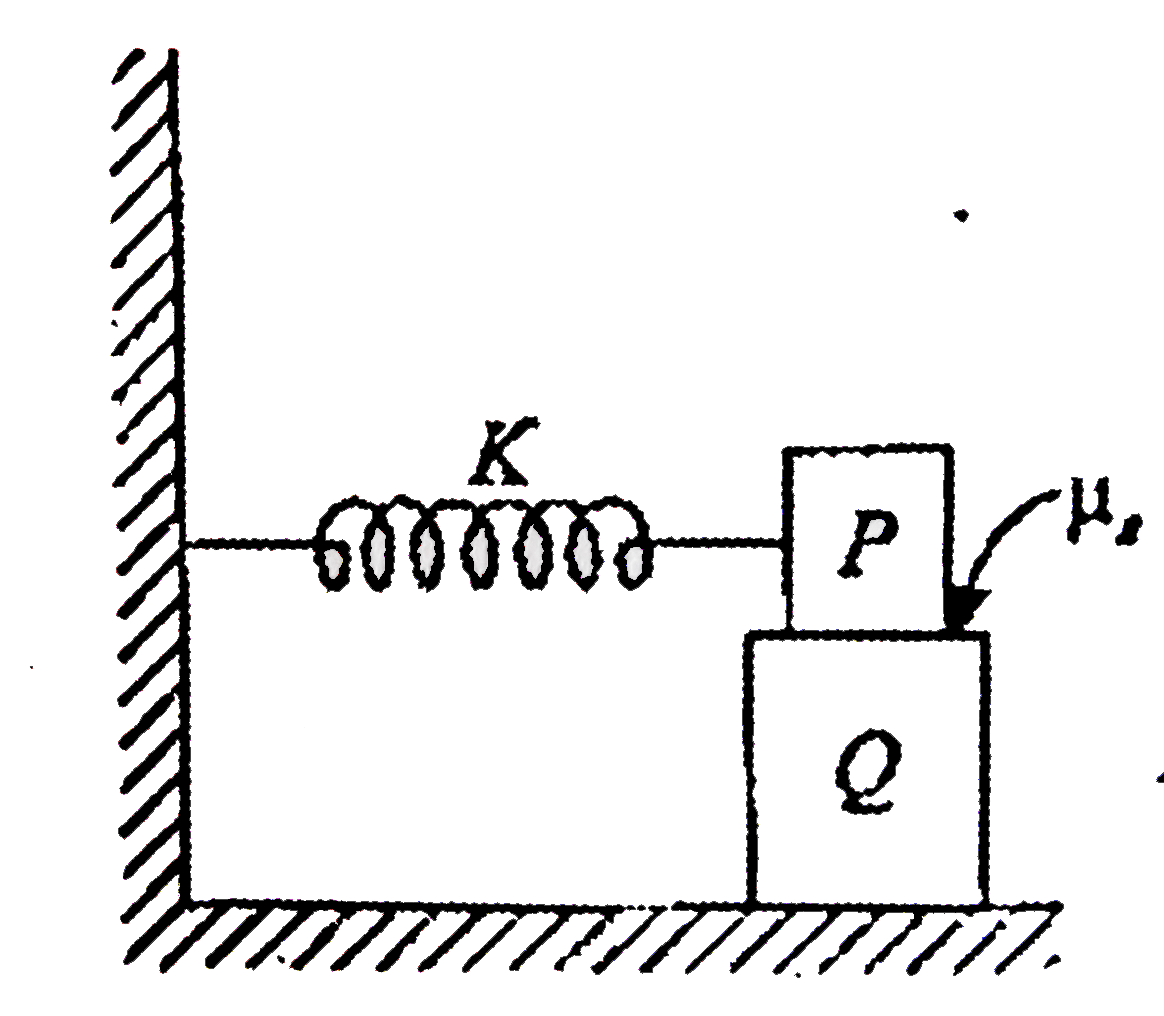 A13KA2B23KA2C12KA2D14KA2
A13KA2B23KA2C12KA2D14KA2
Two springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View Solution

