The magnetic field due to a conductor fo unifrom cross section of radius a and carrying a steady current is represented by
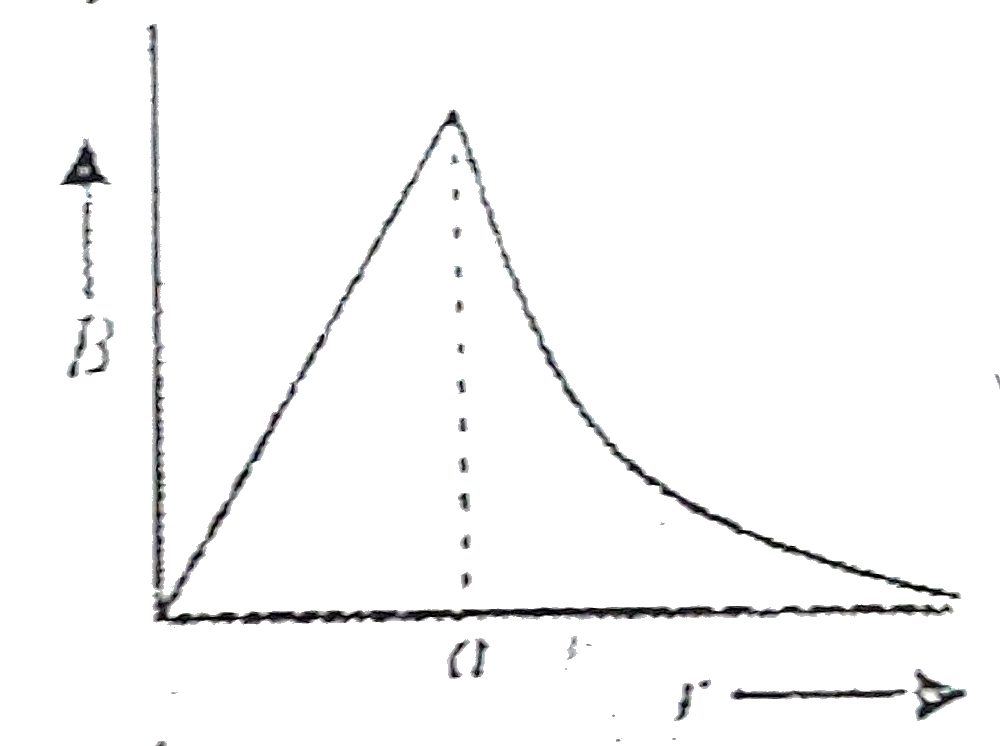
Magnetic field at a point outside the straight conductor is
B=μ0l2πr
i.e.B∞(1/r)(r>a).
Magnetic field at a point lying inside the conductor is B∞r(r<a).

Topper's Solved these Questions
Similar Questions
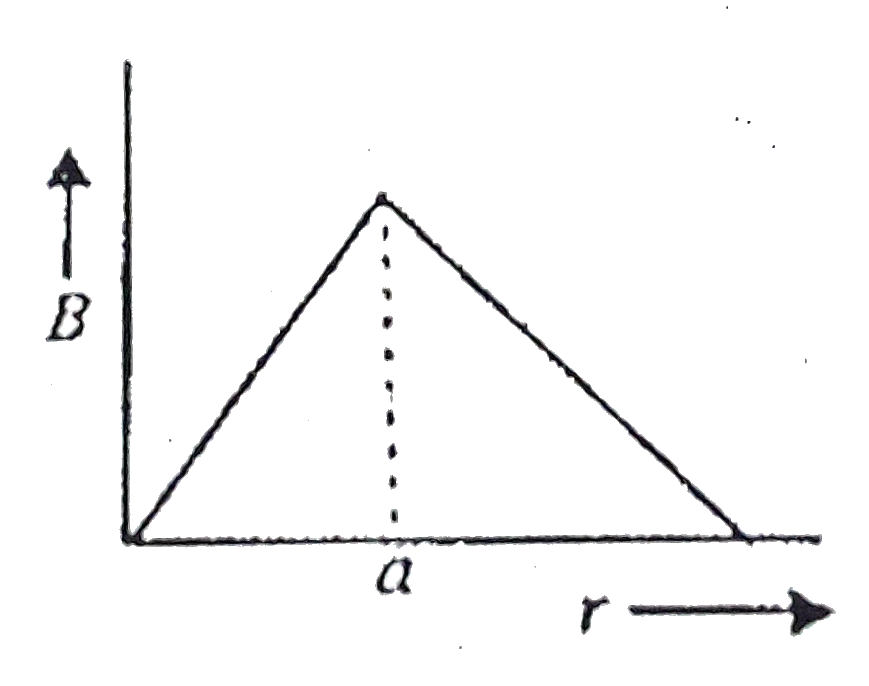
Show graphically the variation of magnetic field due to a straight conductor of uniform cross-section or radius ‘a’ and carrying steady currently as a function of distance r (a > r) from the axis of the conductor.
View Solution(a) State Bio-Savart's law in vector form expressing the magnetic field due to an element →dl carrying current I at a distance r from the element.
(b) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius 'R' carrying a steady current I. Draw the field lines due to the current loop.
View Solution
Knowledge Check
The magnetic field B due to a straight conductor of uniform cross-section of radius 'a' and carrying a steady current varies with the distance 'r' from the centre of conductor as shown in graph .
A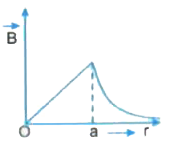 B
B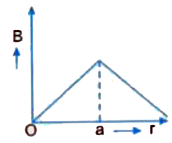 C
C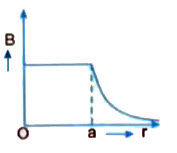 D
D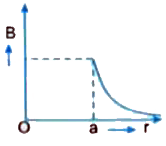
A wire of non-uniform cross-section is carrying a steady current. Along the wire
Acurrent and current density are constantBonly current is constantConly current density is constantDneither current nor current density is a constantThe magnetic field near a current carrying conductor is given by
ACoulomb’s lawBLenz’ lawCBiot-savart’s lawDKirchoff’s law
The adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i)r<a,(ii)r>a.
View SolutionA straight thick long wire of uniform cross-section of radius 5cm is carrying a steady current 5A. Calculate the magnetic field at a point 2cm from the axis of wire, well inside the wire.
View SolutionState the Biot-Savart's law for the magnetic field due to a current carrying element. Use this law to obtain a formula for magnetic field at the centre of a circular loop of radius R carrying a steady current I, sketch the magnetic field lines for a current loop clearly indicating the direction of the field.
View SolutionMagnetic Field due to a Current Carrying Conductor
View SolutionWrite Ampere's circuital law.A long straight wire of a circular cross section (radius a) carrying steady current.Current is uniformly distributed in the wire.Calculate magnetic field inside the region (r<a) in the wire.
View Solution

