A capacitor of capacitance C has potential difference E2 and another capacitor of capacitance C is uncharged. They are joined to form a closed circuit as shown in the figure.
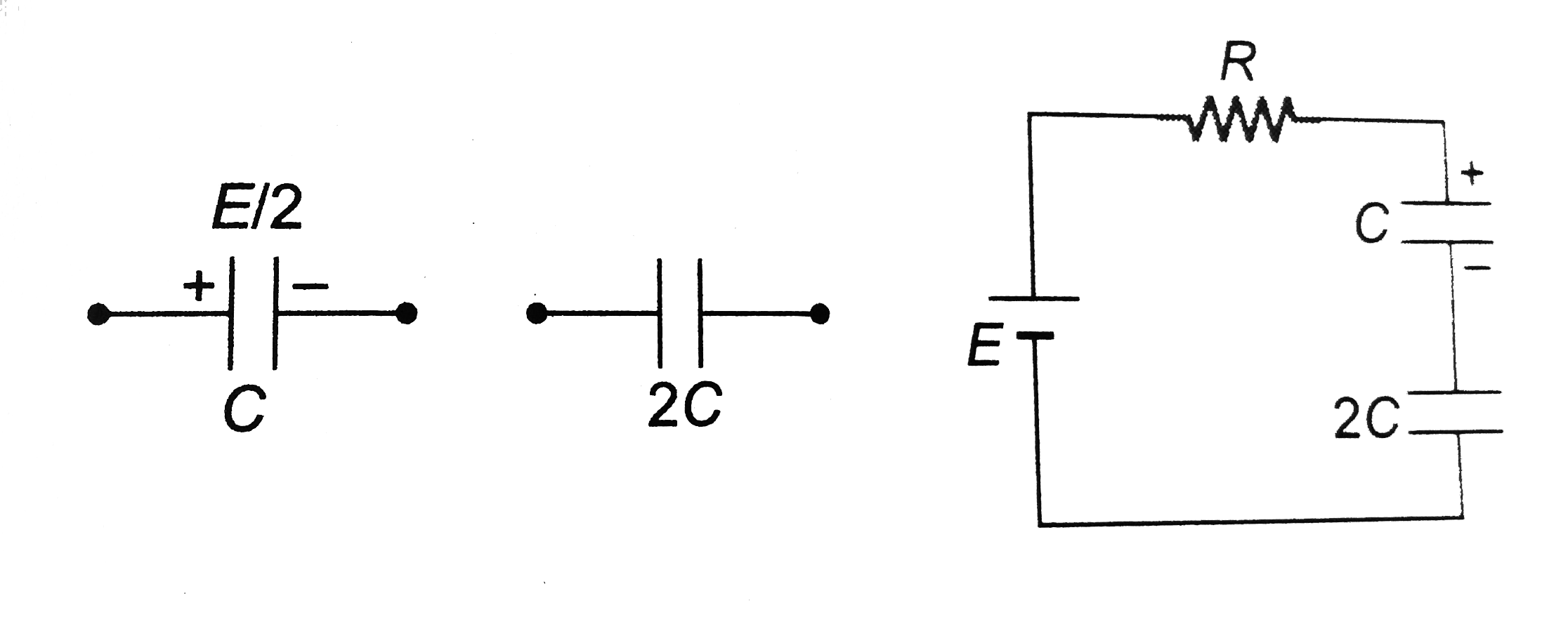
a. Find the current in the circuit at t =0.
b. Find the charge on C as a function of time.
The correct Answer is:B, C
a. At t=0, capacitor is equivalent to a battery of emf E2
Net emf of the circuit =E−E2=E2
Total resistance is R
Therefore, current in the circuit at t=0
would be i=E2R=E2R
b. Let in steady state there is total q charge on C initial charge on C was CE2. Therefore CE2−q with polarities as shown. This is because net charge on lower late of C and of upper plate on 2C should remain constant. Applying looplaw in the circuit in steady state, we have.
E−qC+CE2−q2C=0
∴q=56CE

Therefore charge of C increases from qi=CE2→qf=5CE6 exponentially.
Equivalent time constant would be
τC=(C×2CC+2C)R=23CR
Therefore charge as function of time would be
q=qi+(qf−qi)1−e−tτC)
CE2+CE3(1−e−3t2CR)
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Knowledge Check
A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)VThree uncharged capacitors of capacitance C1,C2 and C3 are connected to one another as shown in figure. The potential at O will be
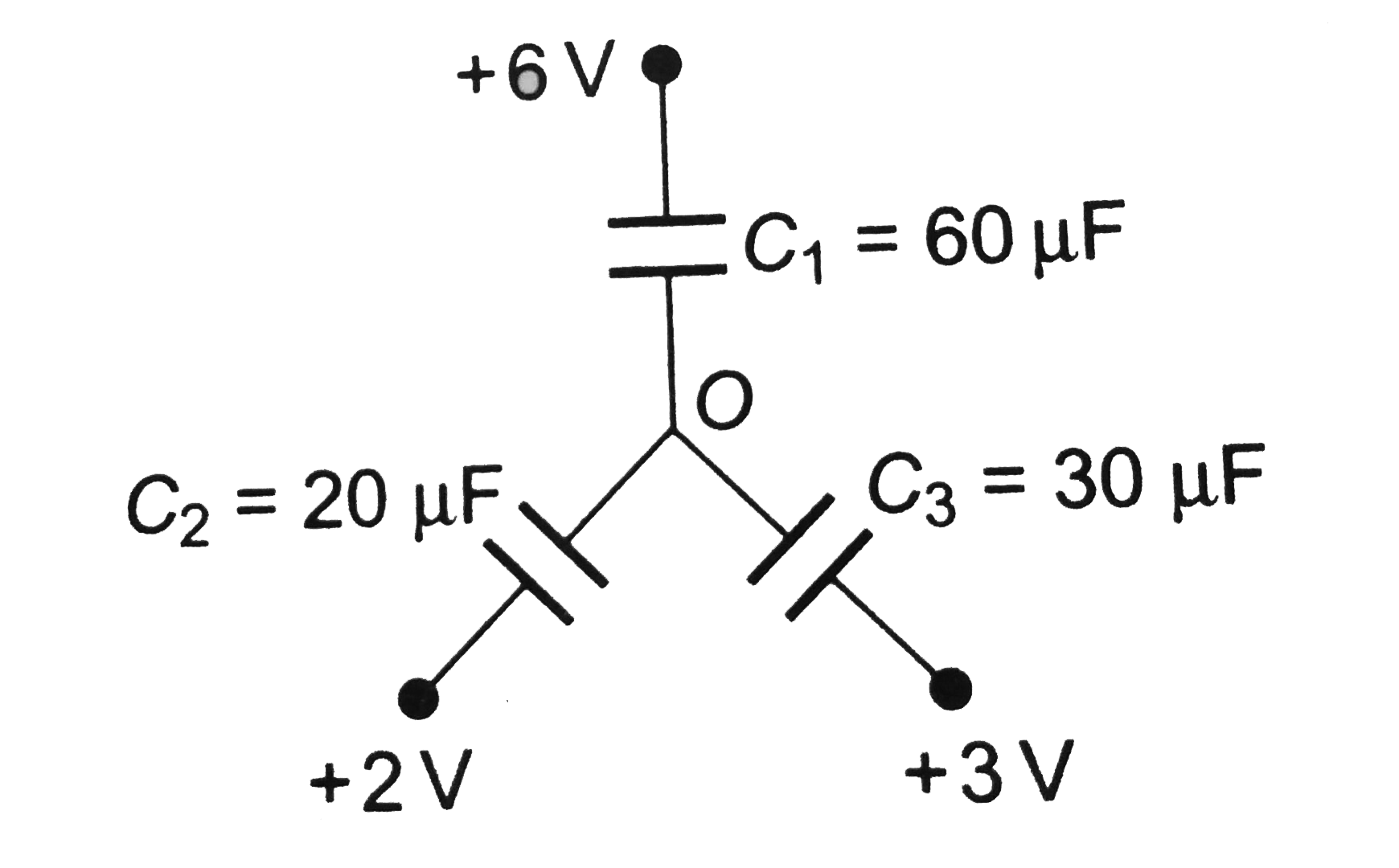 A3VB4911VC4VD311V
A3VB4911VC4VD311VA capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
A12C0V20B13C0V20C16C0V20D18C0V20
Two parallel plate capacitor of capacitance 2C and C are charged to the potentials 2 V and V respectively and are connected in a circuit along with a resistance R as shown in the diagram. The switch k is closed at t=0. Find the current in the circuit as a function of time and total heat produced in the circuit
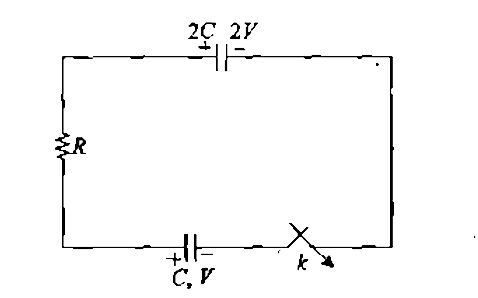
View SolutionA capacitor of capacitance C, which is initially uncharged , is connected with a battery of emf ε. Find the heat dissipated in the circuit during the process of charging .
View SolutionA capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the two capacitors before they are connected .
View SolutionA capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the parallel combination of two capacitors.
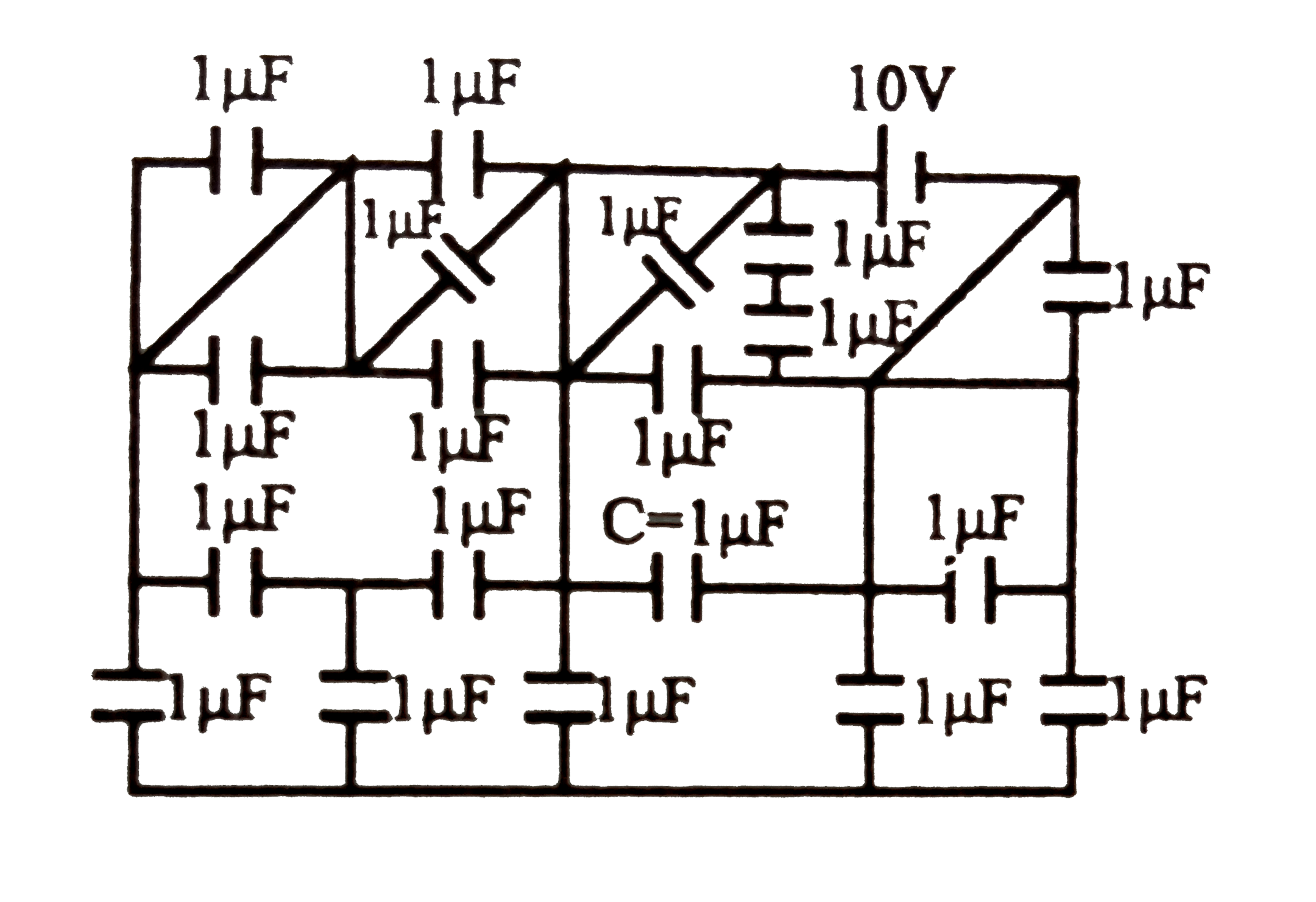
View SolutionIn the circuit shown in figure find
a. the equivalent capacitance and
b. the charge stored in each capacitor.
View Solution