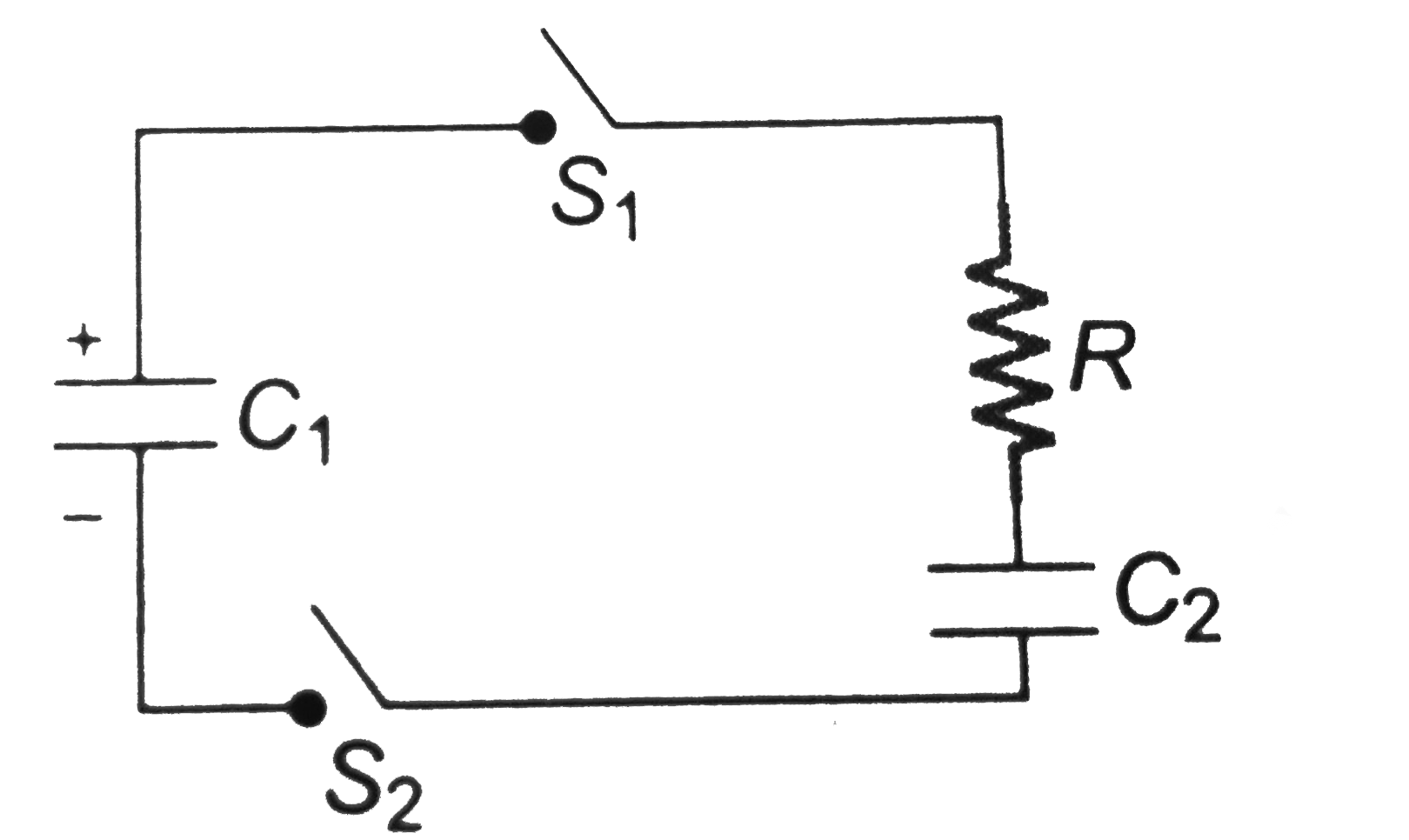
The capactor C1 in the figure initially carries a charge q0. When the i switch S1 and S2 are closed, capacitor C1 is connected to a resistor R and a second capacitor C2, which initially does not carry any charge.
(a) Find the charges deposited on the capacitors in steady state and the current through R as a function of time.
(b) What is heat lost in the resistor after a long time of closing the switch?
The correct Answer is:A, B, C
In steady state, capacitors will be in parallel. Charge will distribute in direct ratio of their capacity.
∴q1=(C1C1+C2)q0
and q2=(C2C1+C2)q0
Initial emf in the circuit is potential difference across capacitor C1 or q0C1.
Therefore, initial current would be
i0=q0/C1R=q0C1R
Current as function of time will be i=i0e−t/τC
Here, τC=(C1C2C1+C2)R
b. Ui=12q20C1 and Uf=12q20C1+C2
Heat lost in the resistor
=Ui−Uf=q202[C2C1(C1+C3)]
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
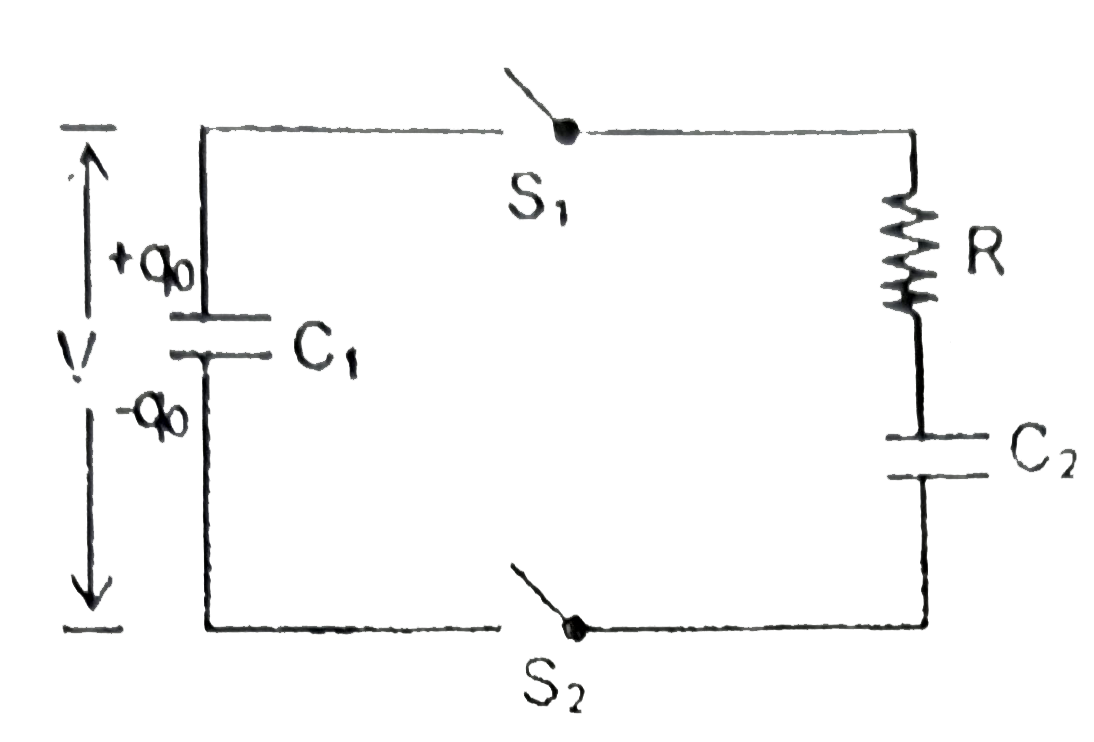
The capacitor C1 in the figure initially carries a charge q0. When the switch S1 and S2 are shut, capacitor C1 is connected in series to a resistor R and a second capacitor C2, which initially does not carry any charge.
If the heat lost in the resistor after a long time of closing the switch is q20C2kC1(C1+C2), then Find the value of k.
View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View Solution
Knowledge Check
The capacitor C1 in the figure shown initially carries a charge q0. When the switches S1 and S2 are closed, capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.
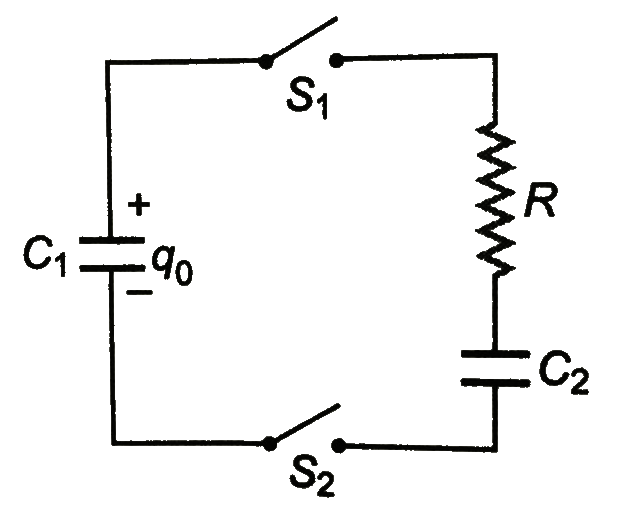
the total head dissipated in the circuit during the discharging process of C1 isAq202C21×CBq202CCq20C22C21Dq202C1C2The capacitor C1 in the figure shown initially carries a charge q0. When the switches S1 and S2 are closed, capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.
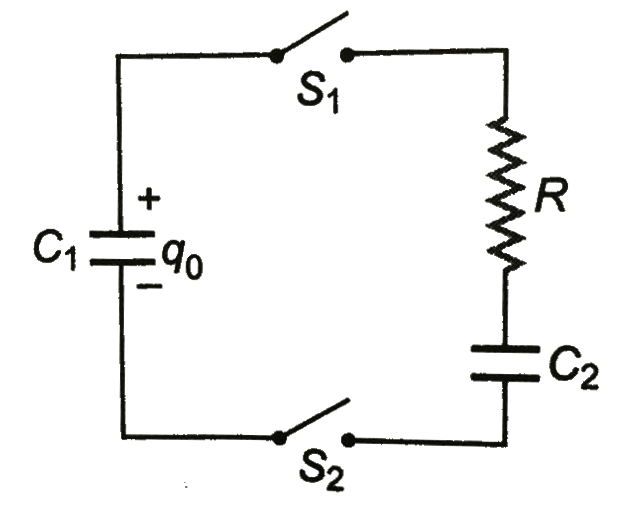
The charge flown through wires as a function of time is
where C=C1C2C1+C2Aq0e−tRC+CC2q0Bq0CC1x[1−e−tRC]Cq0CC1e−tCRDq0e−tRCThe circuit is in a steady state.
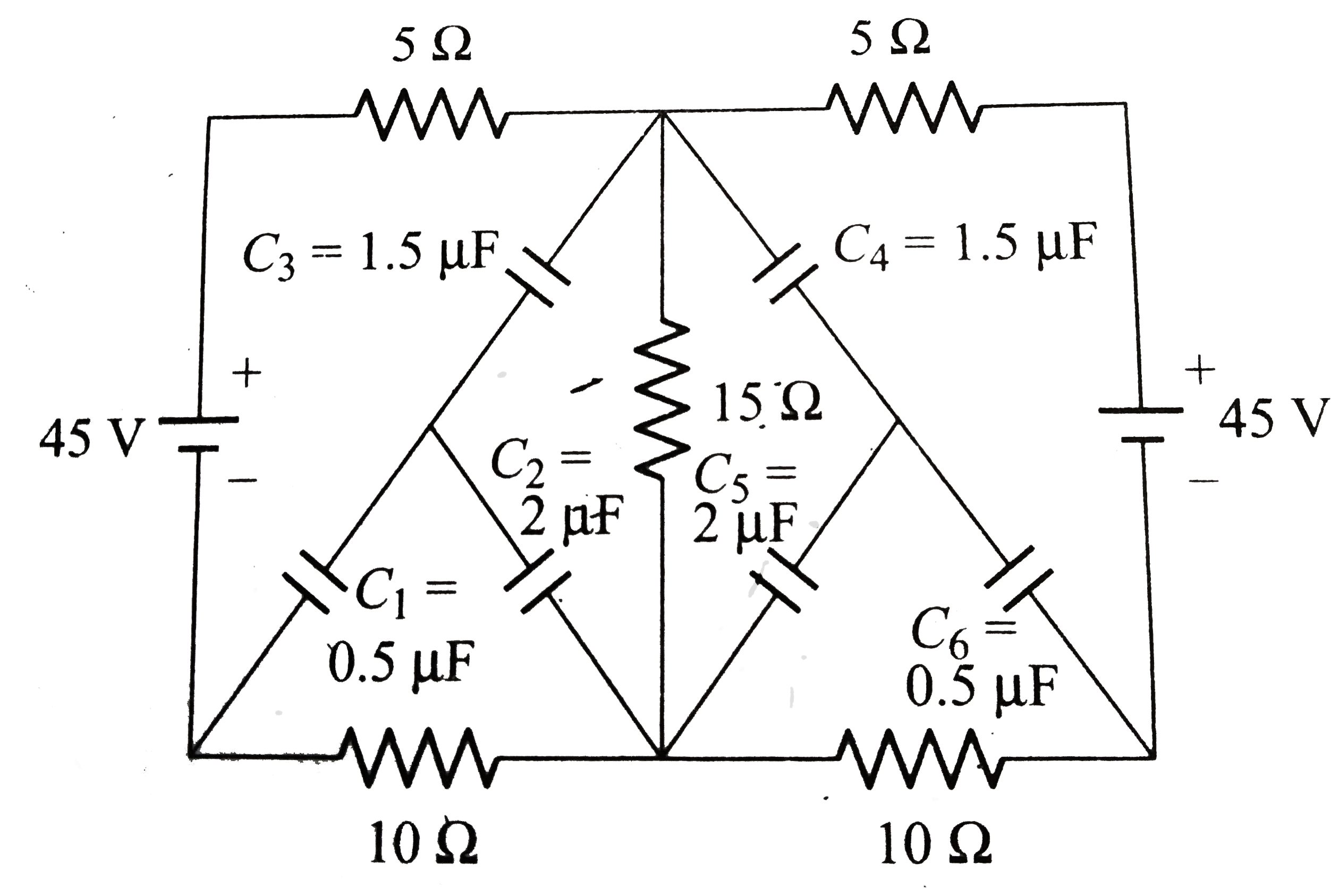
The charge in capacitor C1 isA20μCB30μCC40μCD10μC
The charge on the capacitor is initially zero. Find the charge on the capacitor as a function of time t. All resistors are of equal value R.
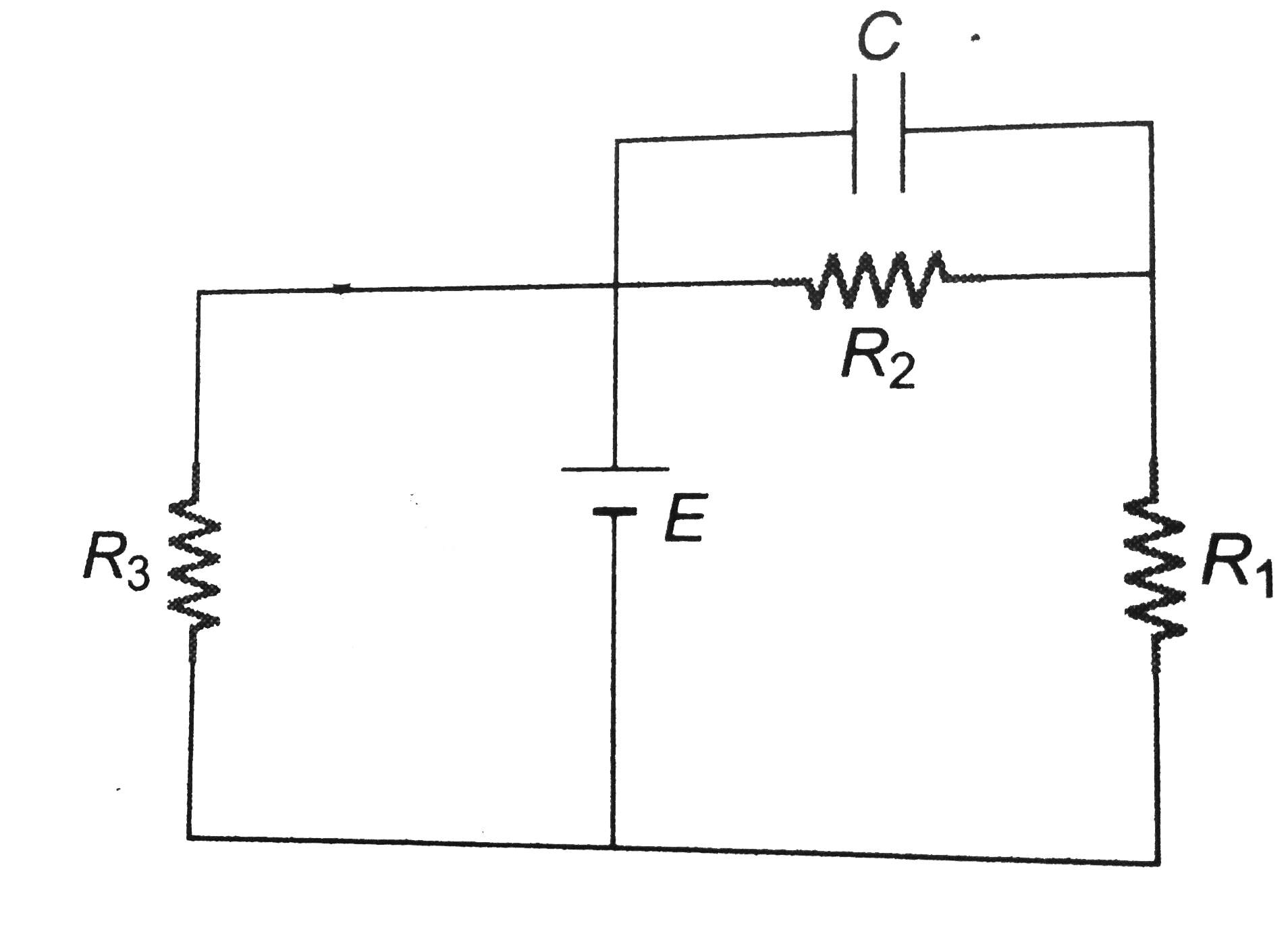
View SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
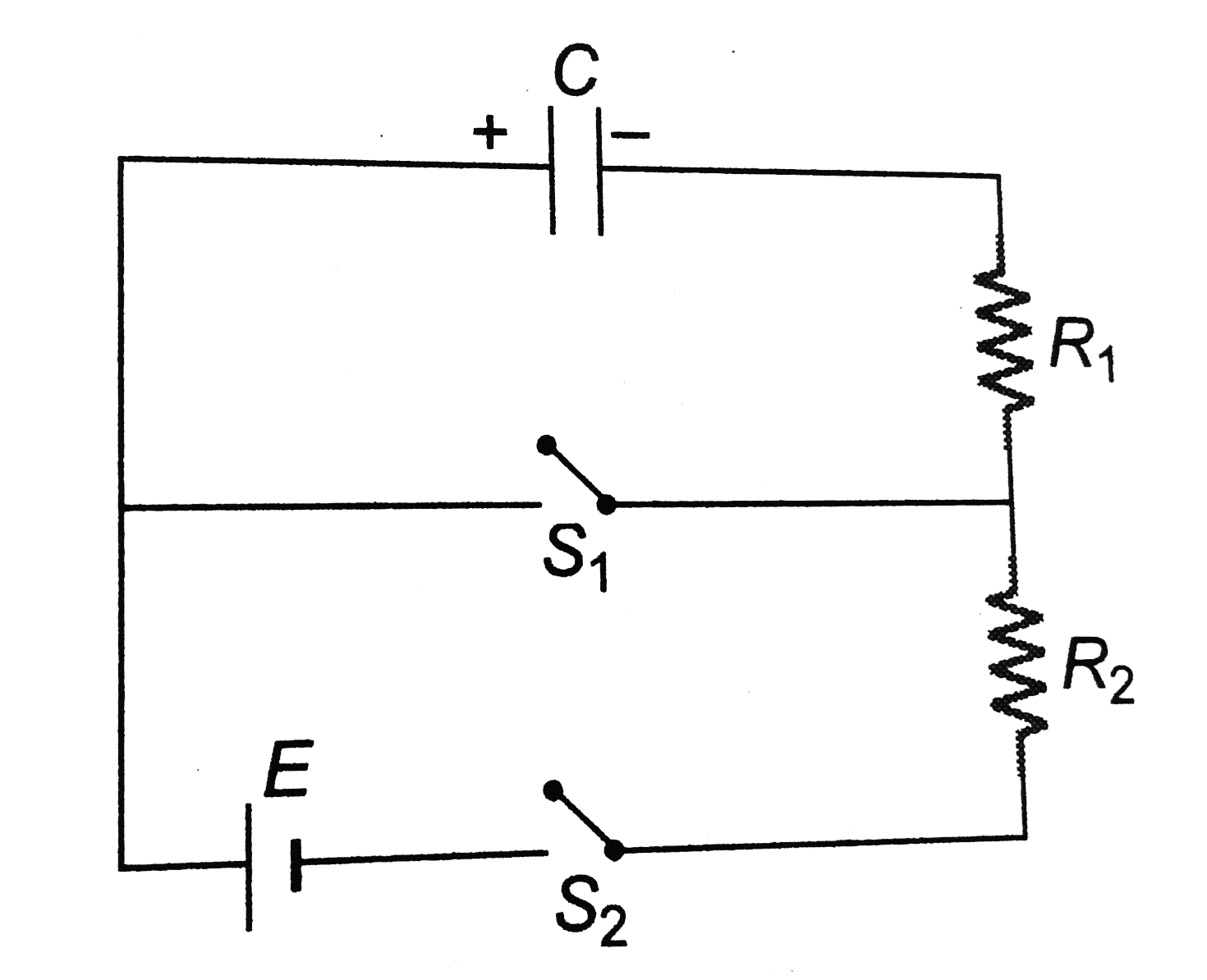
View SolutionThe capacitor shown in figure has been charged to a potential difference of V volt, so that it carries a charge CV with both the switches S1andS2 remaining open. Switch S1 is closed at t=0. At t=R1C switch S1 is opened and S2 is closed. Find the charge on the capacitor at t=2R1C+R2C.
View SolutionThe circuit is in a steady state.
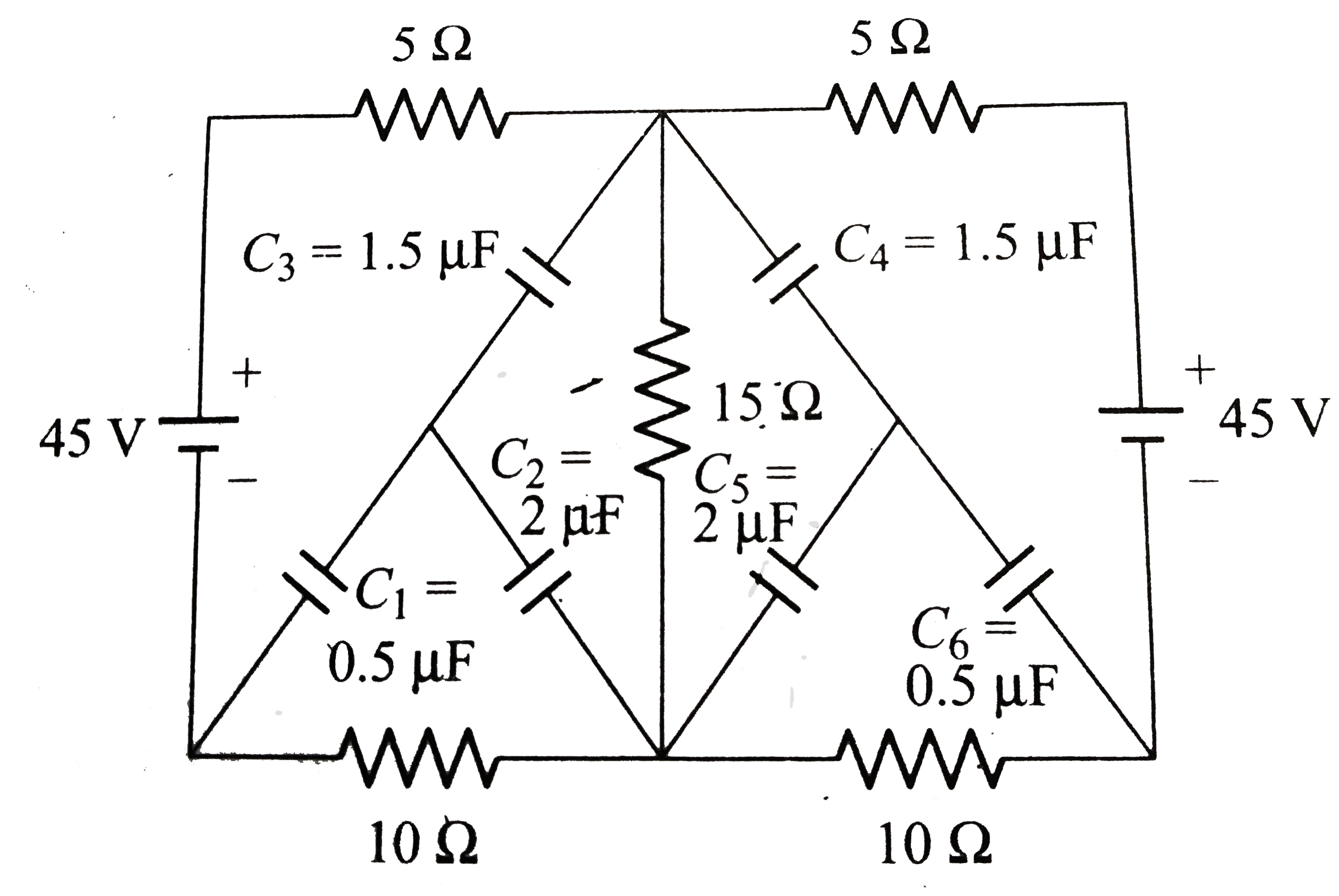
The charge in capacitor C2 is
View SolutionCapacitor C1 is connected to a battery and charged till the magnitude of the charge on each plate is q0. Then, the battery is disconnected and C1 is connected to two other uncharged capacitors C2andC3 as shown in figure. Final charges on the capacitors (q1,q2andq3) are related by .
View Solution
