A 1μF capacitor and a 2µF capacitor are connected in series across a 1200V supply line.
a. Find the charge on each capacitor and the voltage across them.
b. The charged capacitors are disconnected from the line and from each other and reconnected with terminals of like sign together. Find the final charge on each and the voltage across them.
Cnet=C1C2C1+C2=23μF
qnet=CnetV
=(23μF)(1200V)
=800μC
In series q remains same.
∴q1=q2=800μC
V1=q1C1=800V
and V2=q2C2=400V
b. Now, total charge will become 1600μC. This will now distribute in direct ratio of capacity.
∴q1q2=C1C2=12
q1=(13)=(1600)=16003μC
q2=(23)(1600)=(32003)μC
They will have a common potential (in parallel) given by
V=Total chargeTotal capacity
=1600μC3μF
=16003V
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
A 4.00μF capacitor and a 6.00μF capacitor are connected in parallel across a 660V supply line
(a) Find the charge on each capacitor and the voltage across each.
(b) The charged capacitors are disconnected from the line and from each other, and reconnected to each other with terminals of unlike sign together. Find the final charge on each and the voltage across each.
View SolutionFind charge on each capacitor

View Solution
Knowledge Check
Let q be the charge on the capacitor at any time t. The voltage V across the capacitor is
AVmsinωt=qCBVmcosωt=2VCCVmcosωt=q2CDVmsinωt=2qCFigure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?
 A6μCB8μCC10μCD12μC
A6μCB8μCC10μCD12μC
Find charge on each capacitor.
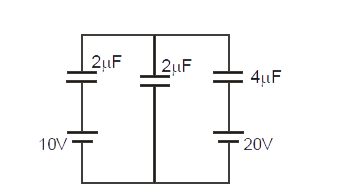
View SolutionFind charge on each capacitor.
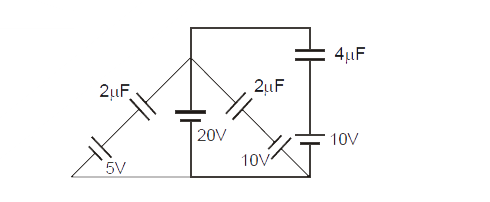
View SolutionFind charge in each capacitor:
View SolutionFind charge in each capacitor:
View SolutionFind charge on each capacitor and potential difference across each capacitor .

View SolutionA network of four capacitors of 6 μF each is connected to a 240 V supply. Determine the charge on each capacitor.
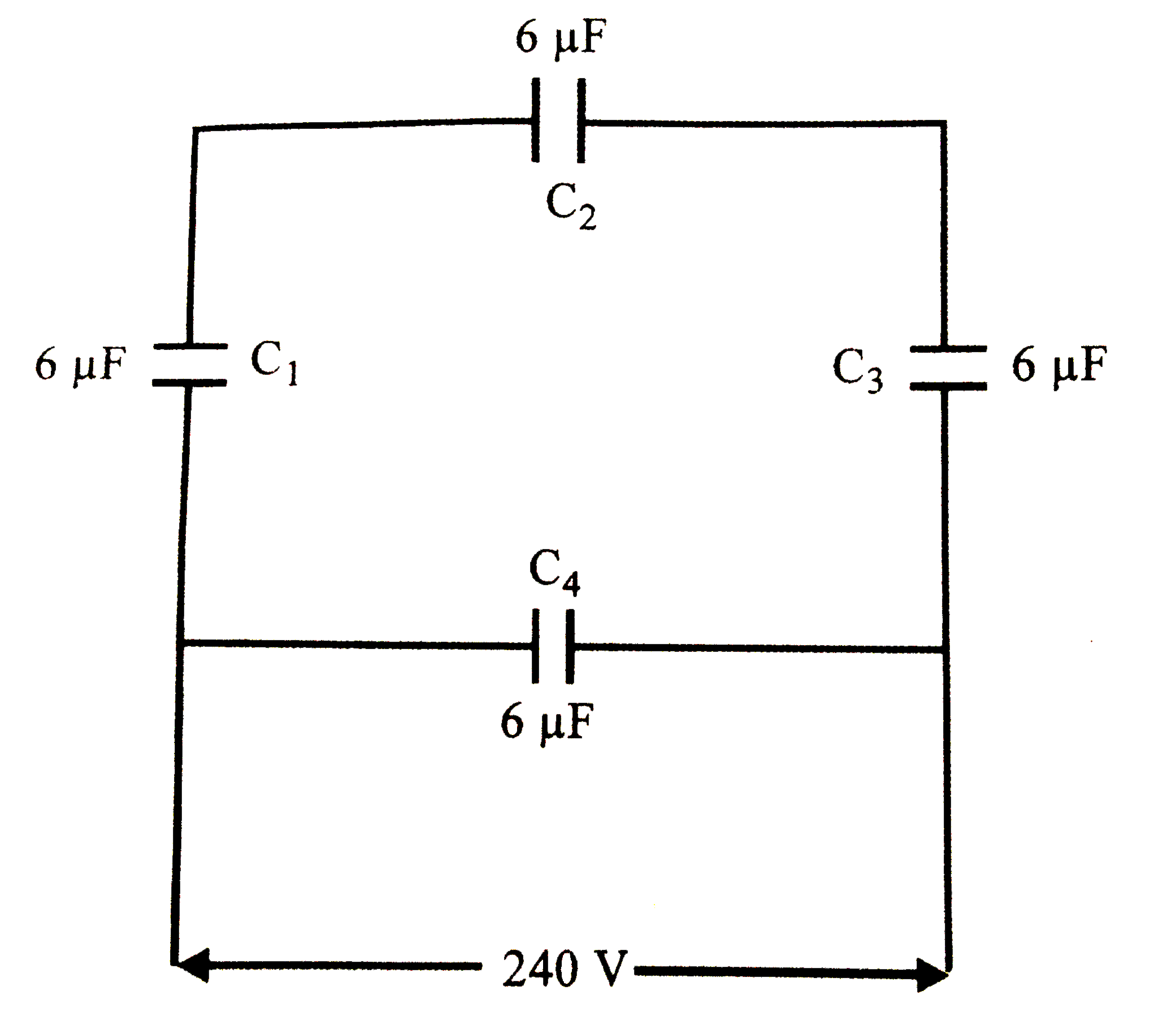
View Solution
