Two, capacitors A and B are connected in series across a 100V supply and it is observed that the potential difference across them are 60V and 40V. A capacitor of 2p.F capacitance is now connected in parallel with A and the potential difference across B rises to 90V. Determine the capacitance of A and B
The correct Answer is:B, D
To solve the problem, we need to determine the capacitances of capacitors A and B based on the given conditions. Let's break down the solution step by step.
Step 1: Understand the Series Connection
When capacitors are connected in series, the total voltage across them is equal to the sum of the voltages across each capacitor. Given:
- Voltage across A (V_A) = 60 V
- Voltage across B (V_B) = 40 V
- Total Voltage (V_total) = 100 V
Step 2: Use the Voltage Relationship
From the information provided, we can write:
VA+VB=Vtotal
60V+40V=100V
This confirms that the voltage distribution is correct.
Step 3: Relate the Capacitances Using Voltage
In a series connection, the charge (Q) on each capacitor is the same. We can use the relationship:
Q=CA⋅VA=CB⋅VB
This implies:
CACB=VBVA=4060=23
Let CB=3x and CA=2x.
Step 4: Find the Total Capacitance
The total capacitance Ctotal for capacitors in series is given by:
1Ctotal=1CA+1CB
Substituting the values:
1Ctotal=12x+13x
Finding a common denominator:
1Ctotal=3+26x=56x
Thus:
Ctotal=6x5
Step 5: Analyze the Second Condition
Now, a capacitor of 2 pF is connected in parallel with capacitor A. The new voltage across B becomes 90 V. The voltage across A must then be:
V′A=Vtotal−V′B=100V−90V=10V
Step 6: Update the Capacitance of A
The new capacitance C′A when the 2 pF capacitor is added in parallel is:
C′A=CA+2 pF
Step 7: Relate the New Voltages
Using the new voltage across A (10 V) and the new voltage across B (90 V):
Since the charge remains the same:
Q=C′A⋅V′A=CB⋅V′B
Substituting the values:
(CA+2)⋅10=CB⋅90
Step 8: Substitute CB and Solve
From our earlier relationship:
CB=3x
So we have:
(2x+2)⋅10=3x⋅90
Expanding and simplifying:
20x+20=270x
250x=20
x=20250=225 F
Step 9: Calculate Capacitances
Now substituting back to find CA and CB:
CA=2x=2⋅225=425 F=0.16 µF
CB=3x=3⋅225=625 F=0.24 µF
Final Answer
- Capacitance of A, CA=0.16 µF
- Capacitance of B, CB=0.24 µF
---
When capacitors are connected in series, the total voltage across them is equal to the sum of the voltages across each capacitor. Given:
- Voltage across A (V_A) = 60 V
- Voltage across B (V_B) = 40 V
- Total Voltage (V_total) = 100 V
From the information provided, we can write:
VA+VB=Vtotal
60V+40V=100V
This confirms that the voltage distribution is correct.
In a series connection, the charge (Q) on each capacitor is the same. We can use the relationship:
Q=CA⋅VA=CB⋅VB
This implies:
CACB=VBVA=4060=23
Let CB=3x and CA=2x.
The total capacitance Ctotal for capacitors in series is given by:
1Ctotal=1CA+1CB
Substituting the values:
1Ctotal=12x+13x
Finding a common denominator:
1Ctotal=3+26x=56x
Thus:
Ctotal=6x5
Now, a capacitor of 2 pF is connected in parallel with capacitor A. The new voltage across B becomes 90 V. The voltage across A must then be:
V′A=Vtotal−V′B=100V−90V=10V
The new capacitance C′A when the 2 pF capacitor is added in parallel is:
C′A=CA+2 pF
Using the new voltage across A (10 V) and the new voltage across B (90 V):
Since the charge remains the same:
Q=C′A⋅V′A=CB⋅V′B
Substituting the values:
(CA+2)⋅10=CB⋅90
From our earlier relationship:
CB=3x
So we have:
(2x+2)⋅10=3x⋅90
Expanding and simplifying:
20x+20=270x
250x=20
x=20250=225 F
Now substituting back to find CA and CB:
CA=2x=2⋅225=425 F=0.16 µF
CB=3x=3⋅225=625 F=0.24 µF
- Capacitance of A, CA=0.16 µF
- Capacitance of B, CB=0.24 µF
Topper's Solved these Questions
- CAPACITORSBook:DC PANDEYChapter:CAPACITORSExercise:OBJECTIVE_TYPE
Explore 1 Video
- CAPACITORSBook:DC PANDEYChapter:CAPACITORSExercise:OBJECTIVE_TYPE
Explore 1 Video
- ATOMSBook:DC PANDEYChapter:ATOMSExercise:MEDICAL ENTRANCES GALLERY
Explore 42 Videos
- COMMUNICATION SYSTEMBook:DC PANDEYChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
Similar Questions
Two capacitors of capacitance 6uF and 4uF are put in series across a 120V battery. What is the potential difference across the 4uF capacitor?
View SolutionA 100pF capacitor is charged to a potential difference of 80.0V and the charging battery is disconnected. The capacitor is then connected in parallel with a second capacitor. If the potential difference across the first capacitor drops to 35.0 V what is the capacitance of this second capacitor?
View Solution
Knowledge Check
Two capacitors 3μF and 6μF are connected in series across a potential difference of 120V. Then the potential difference across 3μF capacitor is:
A40VB60VC80VD100VIf V denotes te potential difference across the plate of a capacitor of capacitance C, the dimensions of CV2 are
ANot expressible in MLTBMLT−2CM2LT−1DML2T−2Two capacitors of capacitances 10μFand20μF are connected in series across a potential difference of 100V. The potential difference across each capacitor is respectively
A66.67 V, 33.33 VB60 V, 40 VC50 V, 50 VD90 V, 10 V
A 220 V AC supply is connected between points A and B.
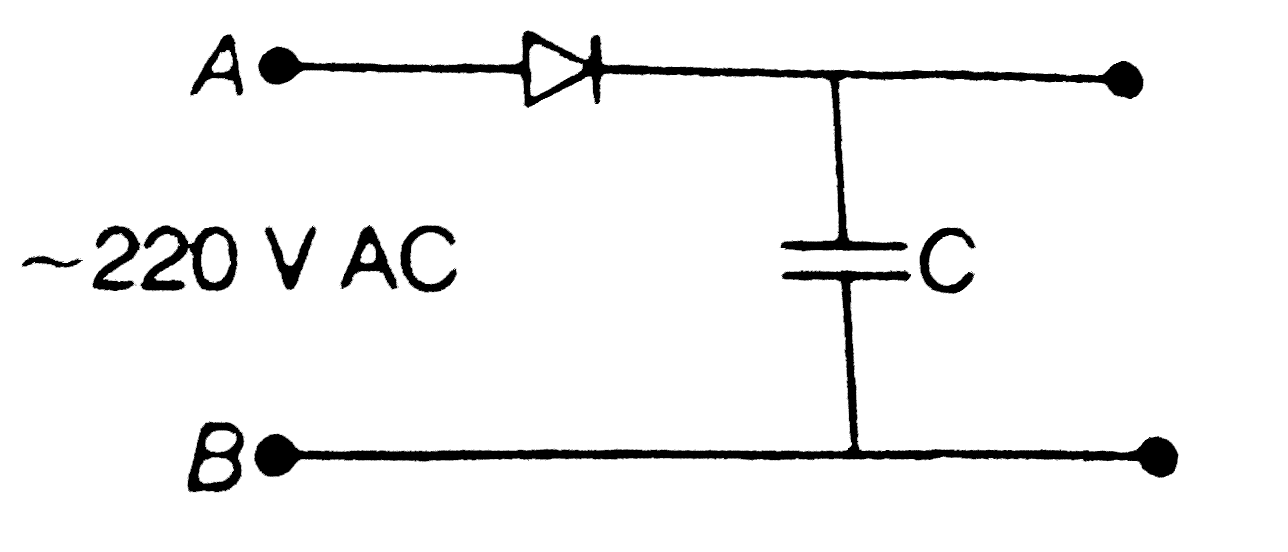
What will be potential difference across capacitor C ?
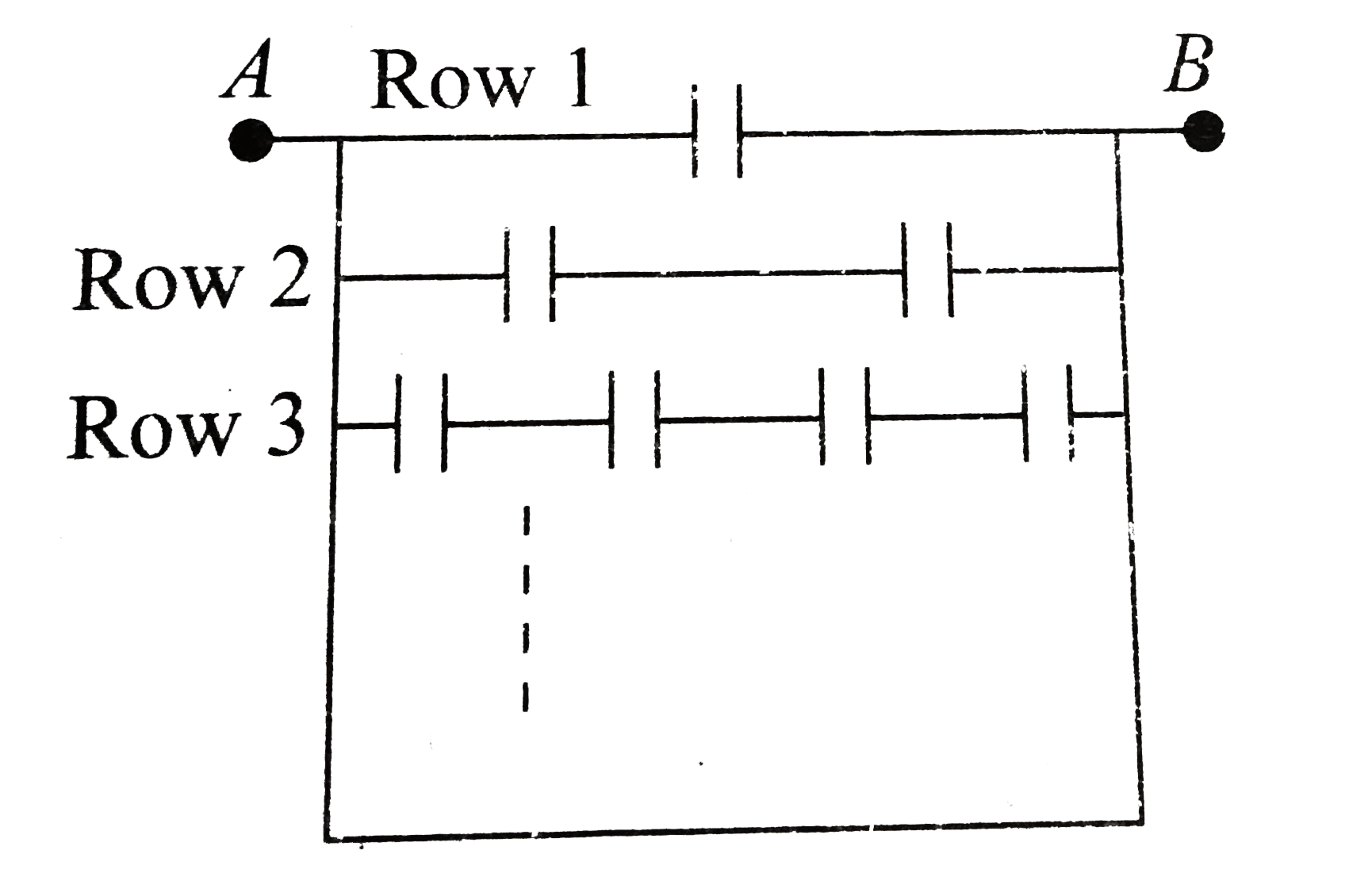
View SolutionRows of capacitors containing 1, 2, 4, 8, ……., ∞ capacitors, each of capacitance 2F, are connected in parallel as shown in figure. The potential difference across AB is 10 V, then
View SolutionPotential difference of 11 V is applied across three capacitors of capacitance 1μF,2μFand3μF connected in series. Potential difference across capacitor of 1μF is:
View SolutionA 220 V AC supply is connected between points A and B . What will be the potential difference V across the capacitor ?

View SolutionRows of capacitors 1,2,4,8…..∞ capacitors, each of capacitance 2μF, are connected in parallel as shown in figure. The potential difference across AB = 10 V, then

View Solution