In figure, battery B supplies 12V. Find the charge on each capacitor
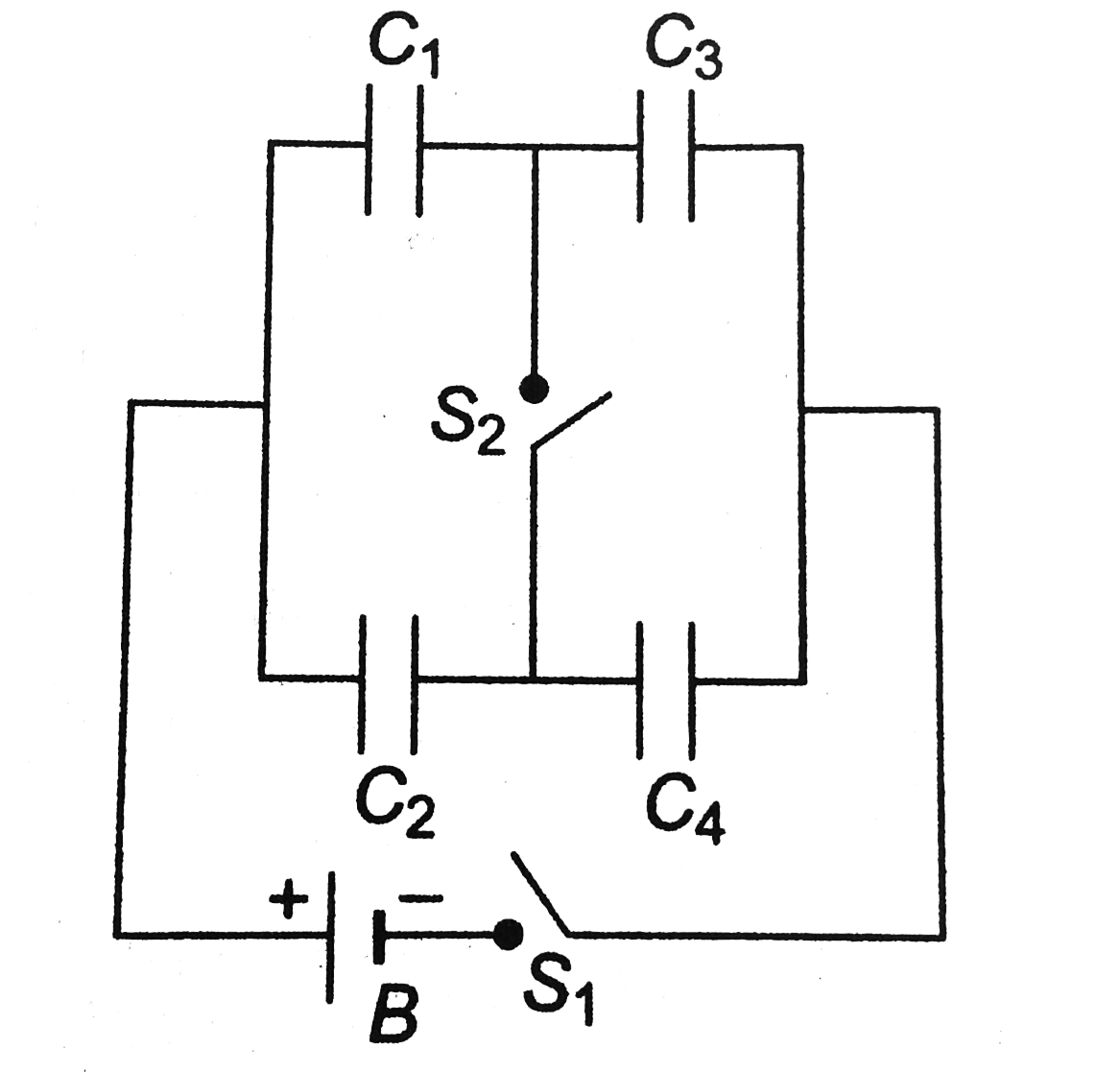
(a) first when only switch S1 is closed and
(b) later when S2 is also closed.
(Take C1=1.0μF,C2=2.0μF,C3=3.0μF and C4=4.0μF)
The correct Answer is:A, C, D
a.
C13=1×31+3=34μF
C24=2x42+4=43μF
VC1C3=VC2C3=12V
∴q1=q3=(C13)(VC1C3=34×12)=9μC
q2=q4=(C24)(VC2C4=43×12)=16μC
b.
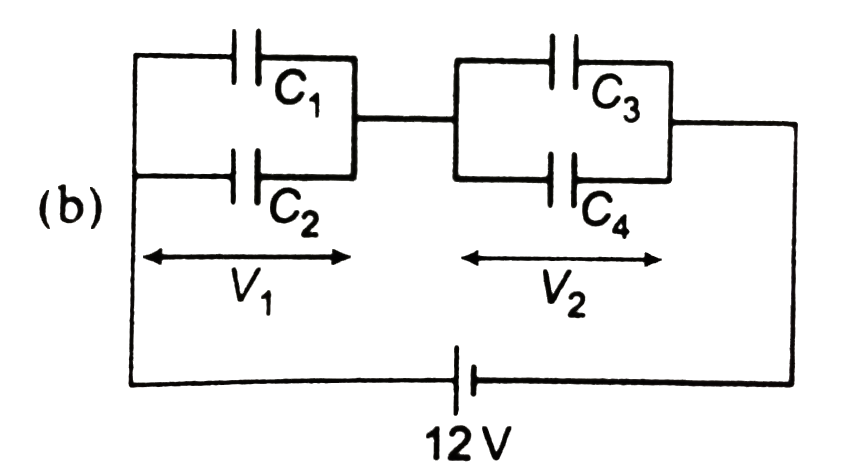
C12=1×21+2=23μF
C34=3×43+4=127μF
V1V2=C34C12=12723=187
∴V1=(1825)(12)=8.64V
V_2=12-8.64=3.36V
now, we can apply q=CV for finding charge on different capacitors.
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Knowledge Check
The charge on a 48 μF capacitor is increased from 0.1 C to 0.5 C. the enerrgy stored in the capacitor increases by
A250 JB2500 JC2.5×106JD2.42×10−6JA potential of V=3000V is applied to a combination of four initially uncharged capacitors as shown in the figure. Capacitors A, B, C and D have capacitances CA=6.0μF,CB=5.2μF,CC=1.5μFandCD=3.8μF, respectiely. If the battery is disconnected, then potential difference across capacitor B is (approximately)
 A3000 VBzeroC530 VD350 V
A3000 VBzeroC530 VD350 VIn each capacitance C1is6.0μF, and each capacitance C2 is 4.0μF.
 .
.
With 420V across a and b the value of Vc−Vd is.A24.6VB46.7VC18VD72V
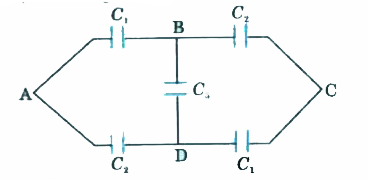
Consider the network of capacitors as shown in the figure. Find equivalent capacitance between points A and C. Assume C1=1μF,C2=0.5μFandC3=1μF.
View SolutionFind the charges on the three capacitors connected to a bettery as shown in figure (31.E1). Take C1=2.0=2.0,μF,C2=4.0,μf,C3=6.0,μFandV=12vo<s.(31-E1). Take C1=2.0μF,C2=4.0μF,C2=6.0μFandV=12vo<s.

View SolutionFind the charges on the three capacitors connected to a bettery as shown in figure (31.E1). Take C1=2.0=2.0,μF,C2=4.0,μf,C3=6.0,μFandV=12vo<s.(31-E1). Take C1=2.0μF,C2=4.0μF,C2=6.0μFandV=12vo<s.

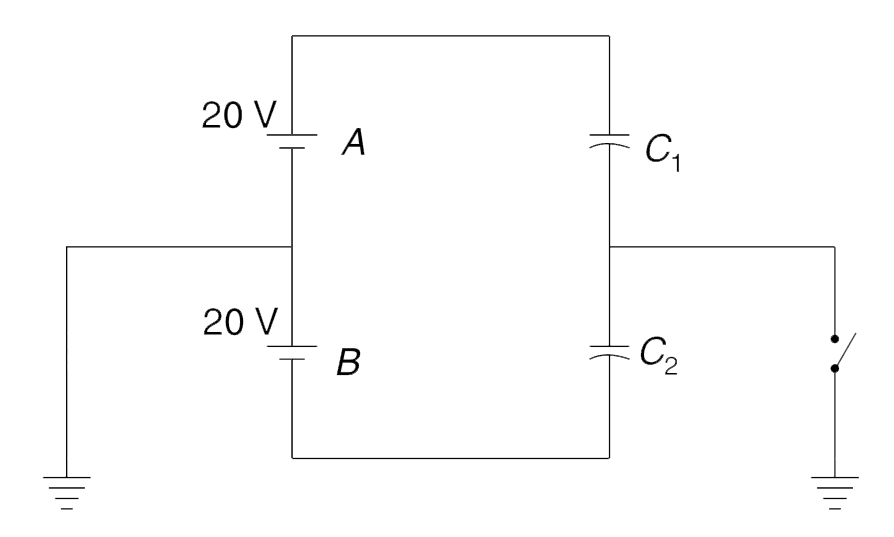
View SolutionIn the circuit shown in the Figure calculate the quantity of charge that flows through the switch after it is closed. Give your answer for following two cases-
(a) C1=C2=2μF
(b) C1=2μF,C2=1μF
View SolutionIn the circuit shown , the emf of each battery is 60V and C1=2μF and C2=3μF. Find the charges that will flow through the sections 1,2 and 3 after the Key is closed.
 .
.
View Solution