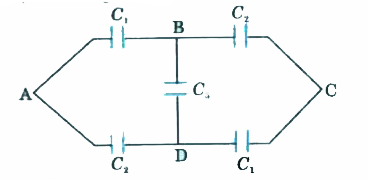
Consider the network of capacitors as shown in the figure. Find equivalent capacitance between points A and C. Assume C1=1μF,C2=0.5μFandC3=1μF.
Video Solution
Text Solution
In the given network of capacitors we can see thatequivalent capacitance cannot be obtained by using the formulae for series and parallel combinations. Apart from that it is nto the case of a balanced Wheatstone bridge. We can still make use of reverse symmetric values of capacitances of the given network to cut short the calculation to a certain extent.
When we connect a battery between the points A and C of circuit, then charge flowing from A to B can be taken as same as flowing from D to C. Similarly charge flowing from A to D will be same as charge flowing form B to C. Flow of charge through the bridge capacitor form B to D can be written accordingly. See the following diagram how total charge Q is distributed in the circuit when a potential difference of V is applied between the points A and C. Here, we must note the fact that, the ratio Q/V will be the equivalent capacitance between A and C, which is required as the final answer to this quesiton.
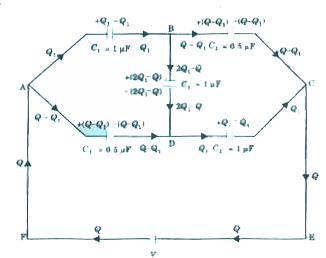
Kirchhoff.s loop Law: Algebraic sum of all the potential differences in a loop must add to zero. This a due to conservative nature of electric field.
On applying Kirchhoff.s law for the loop EFABCE we get the following equation:
V−Q11−Q−Q10.5=0
⇒V−Q1−2Q+2Q1=0⇒V=2Q−Q1 ...(i)
On applying Kirchhoff.s law for the loop ABDA we get the following equation:
−Q11−2Q1−Q1+Q−Q10.5=0
⇒−Q1−2Q1+Q+2Q−2Q1=0
⇒5Q1=3Q⇒Q1=3Q5 ...(ii)
Substituting Q1 from equation (ii) in equation (i) we get the following:
V=2Q−3Q5=7Q5⇒Ceq=QV=57μF
|
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Textbook Exercise)
Explore 11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Additional Exercises)
Explore 23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Conceptual Questions
Explore 37 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
Knowledge Check
Each capacitor shown in the figure is 2μF. Then the equivalent capacitance between points A and B is
 A2μFB4μFC6μFD8μF
A2μFB4μFC6μFD8μFAll the capacitances shown in figure are in μF. Find the equivalent capacitance between A and B.
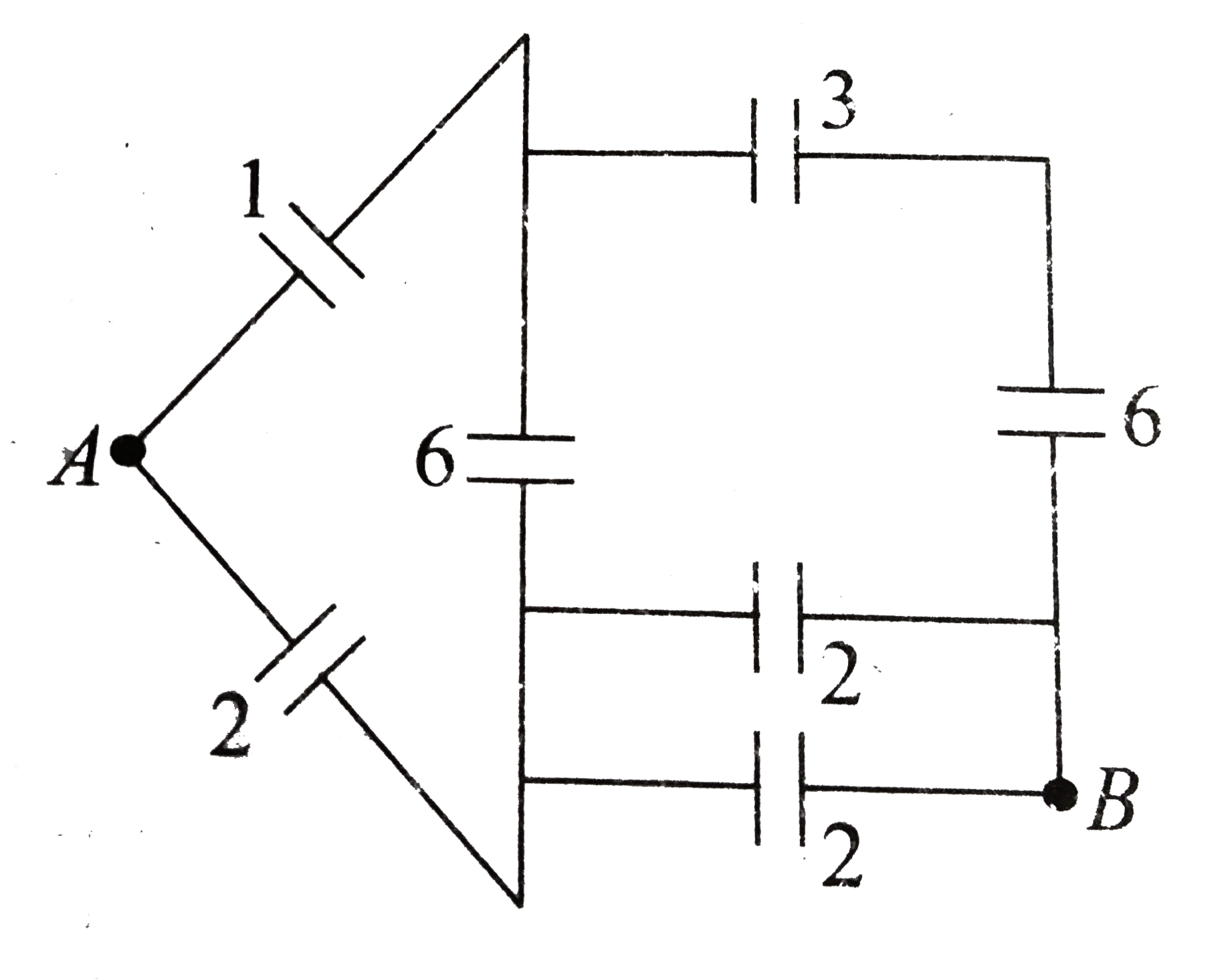 A2μFB3μFC6μFD9μF
A2μFB3μFC6μFD9μFSeven capacitor are connected as shown in the figure.
 .
.
The equivalent capacitance in μF between A and B is.A3.75B8.5C10.25D15
In a given network the equivalent capacitance between A and B is [C1=C4=1μF,C02=C3=2μF]
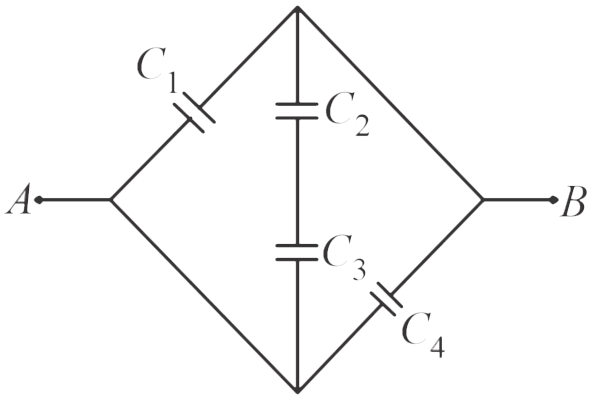
View SolutionFive capacitors each of capacitance 20μF are joined as shown in the figure. The equivalent capacitance between A and C is

View SolutionFind the equivalent capacitane between the points P and Q as shown in Fig. Given C=18μF and C1=12μF
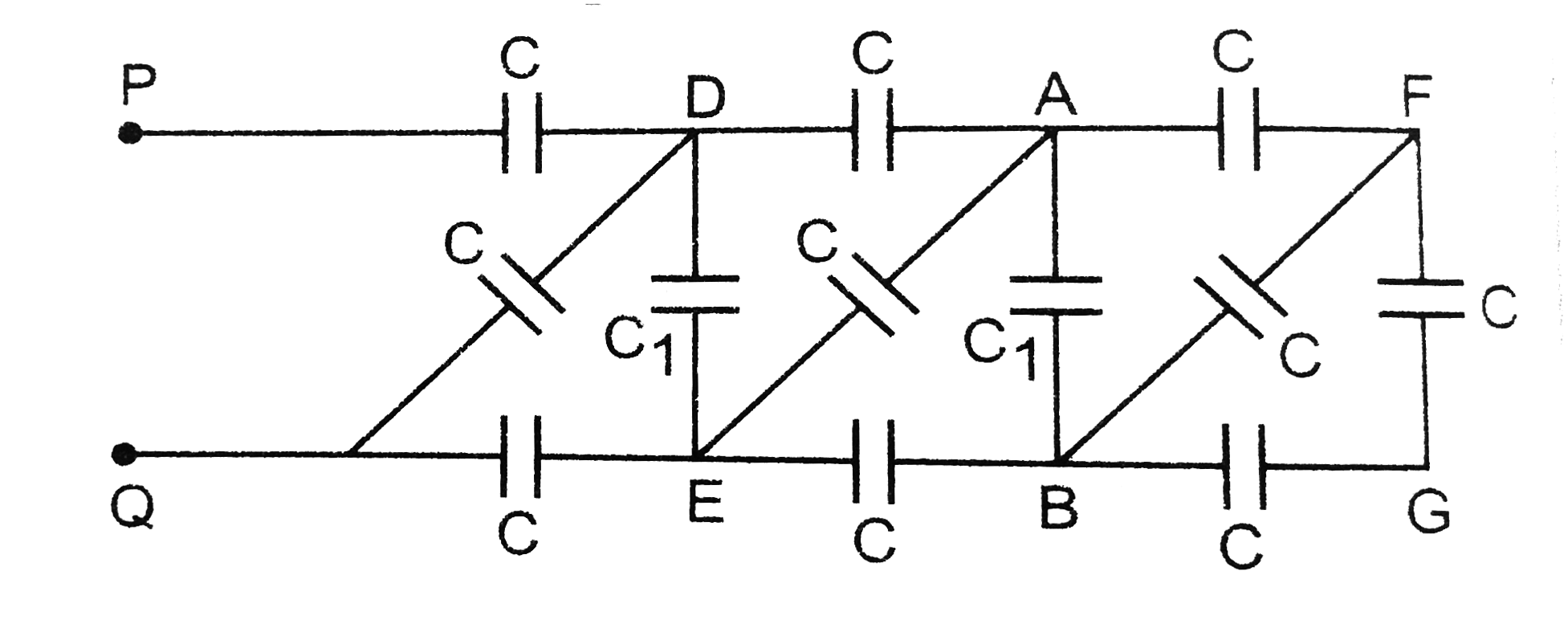
View SolutionIn the arrangement of capacitors shown in the figure, each capacitor is of 9μF, then the equivalent capacitance between the point A and B is
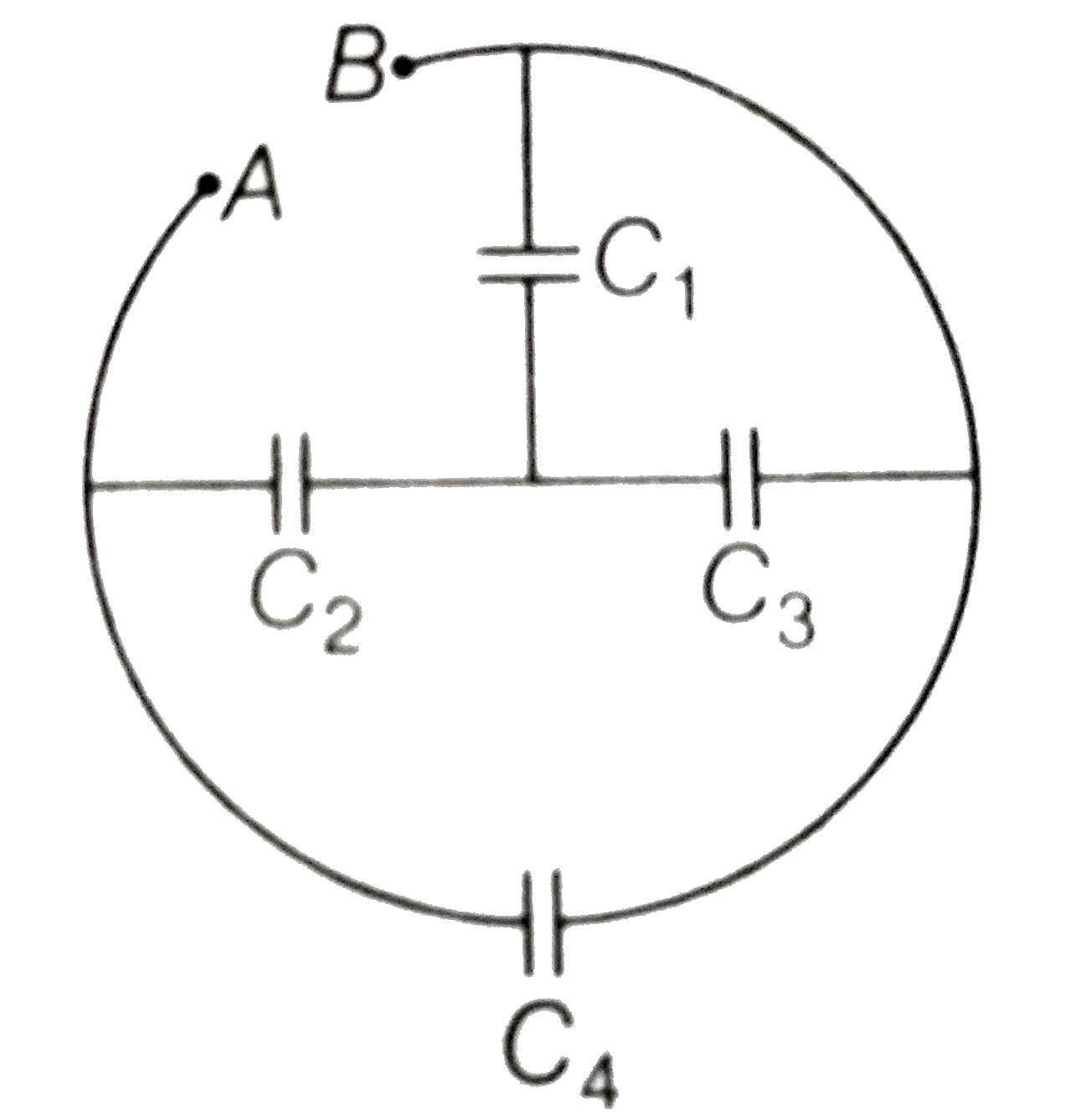
View SolutionFour capacitors, each of 1μF, are joined as shown in Fig.The equivalent capacitance between the points A and B is

View Solution