In the figure shown, a spring mass system is placed on a horizontal smooth surface in between two vertical rigid walls W1 and W2. One end of spring is fixed with wall W1 and other end is attached with mass m which is free to move. Initially, spring is tension free and having natural length l0. Mass m is compressed through a distance a and released. Taking the collision between wall W2 and mass m as elastic and K as spring constant, the average force exerted by mass m on wall W2 in one oscillation of block is

2aKπ
2maπ
aKπ
2aKm
The correct Answer is:A
vmax=ωA=(√Km)a
ΔP=2mv(max)=2m(√Km)a
F=ΔPΔt=ΔPT/2=2ma√k/mπ√m/k=2aKπ

Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionTwo block-spring mass system are moving on smooth horizontal surface as shown in the figure as t=0. find out the minimum time t when the spring is maximum elongated l0 is the natural length of spring.
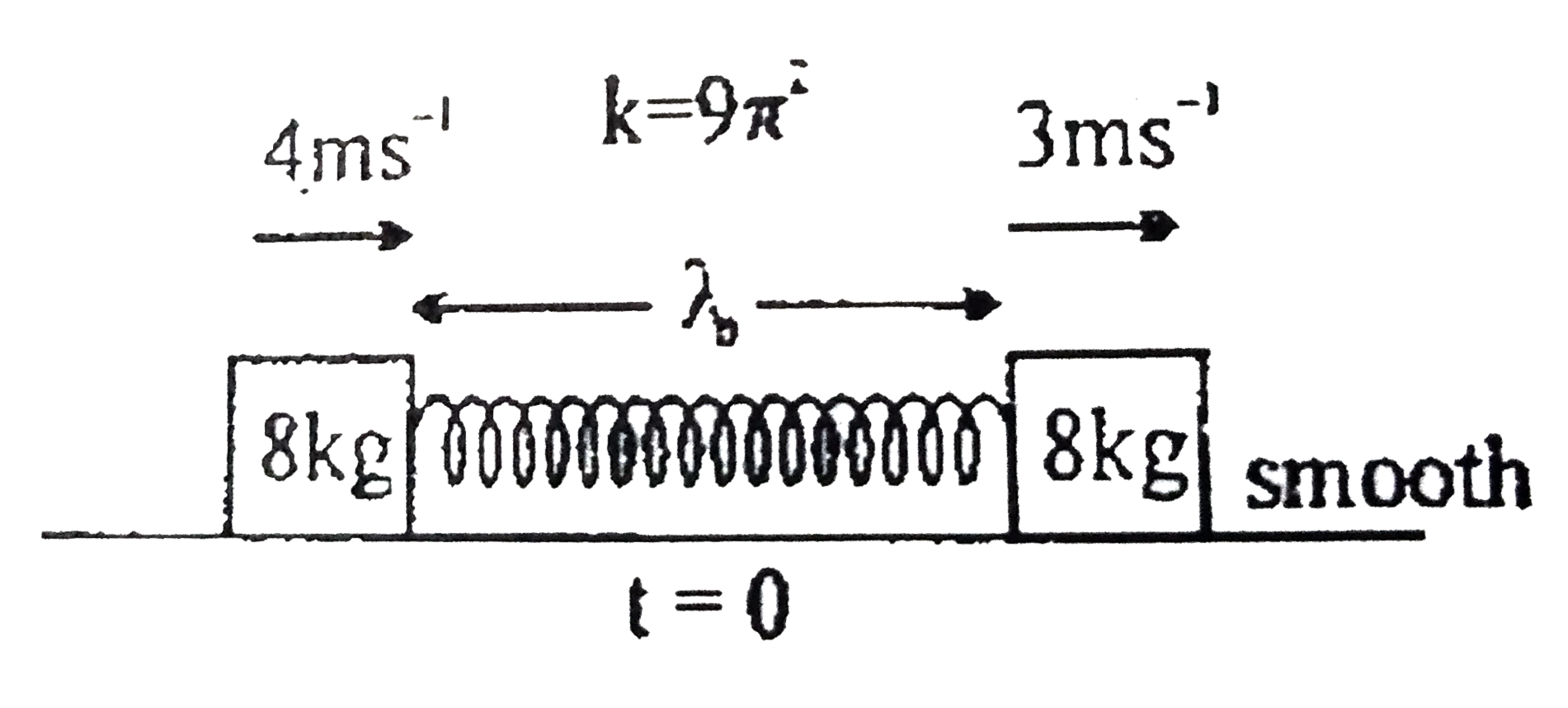
View Solution
Knowledge Check
Mass m is connected with an ideal spring of natural length l whose other end is fixed on a smooth horizontal table. Initially spring is in its natural length l. Mass m is given a velocity 'v' perpendicular to the spring and released . The velocity perpendicular to the spring when its length l+x , will be
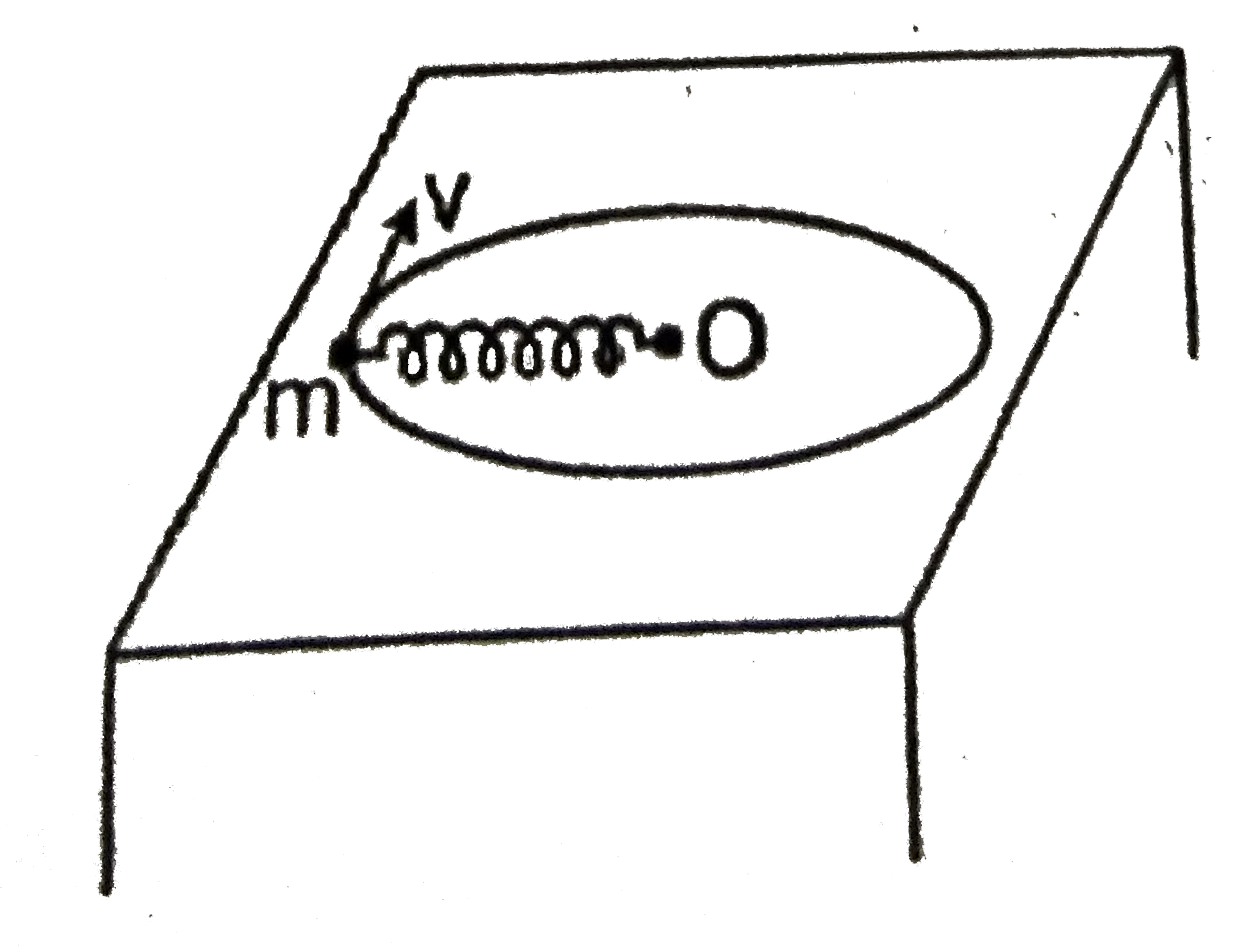 A2vll+xB2v2+ll+xCvll+xDzero
A2vll+xB2v2+ll+xCvll+xDzeroIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
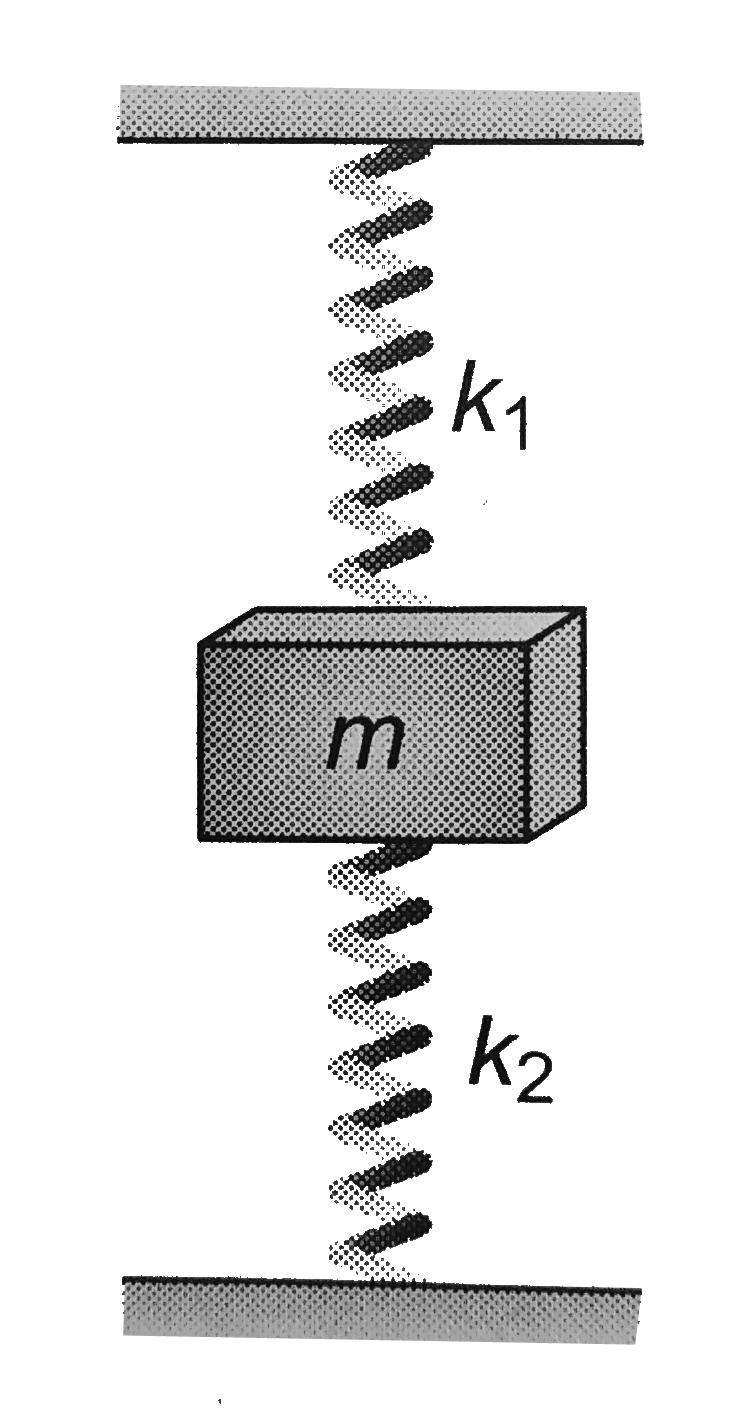 Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated.
Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated.In the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.
 AThe maximum possible speed of the blocks is g(m2−μm1)√k(m1+m2)BThe maximum possible speed of the blocks is g(μm1)√k(m1+m2)CThe maximum possible speed of the blocks if friction is absent is gm2√k(m1+m2)DThe maximum possible speed of the blocks if friction is absent is gm1√k(m1+m2)
AThe maximum possible speed of the blocks is g(m2−μm1)√k(m1+m2)BThe maximum possible speed of the blocks is g(μm1)√k(m1+m2)CThe maximum possible speed of the blocks if friction is absent is gm2√k(m1+m2)DThe maximum possible speed of the blocks if friction is absent is gm1√k(m1+m2)
One end of a spring of force constant k is fixed to a vertical wall and the other to a block of mass m resting on a smooth horizontal surface There is another and wall at a distance x0 from the block The spring is then compressed by 2x0 and released The time taken to at the wall is
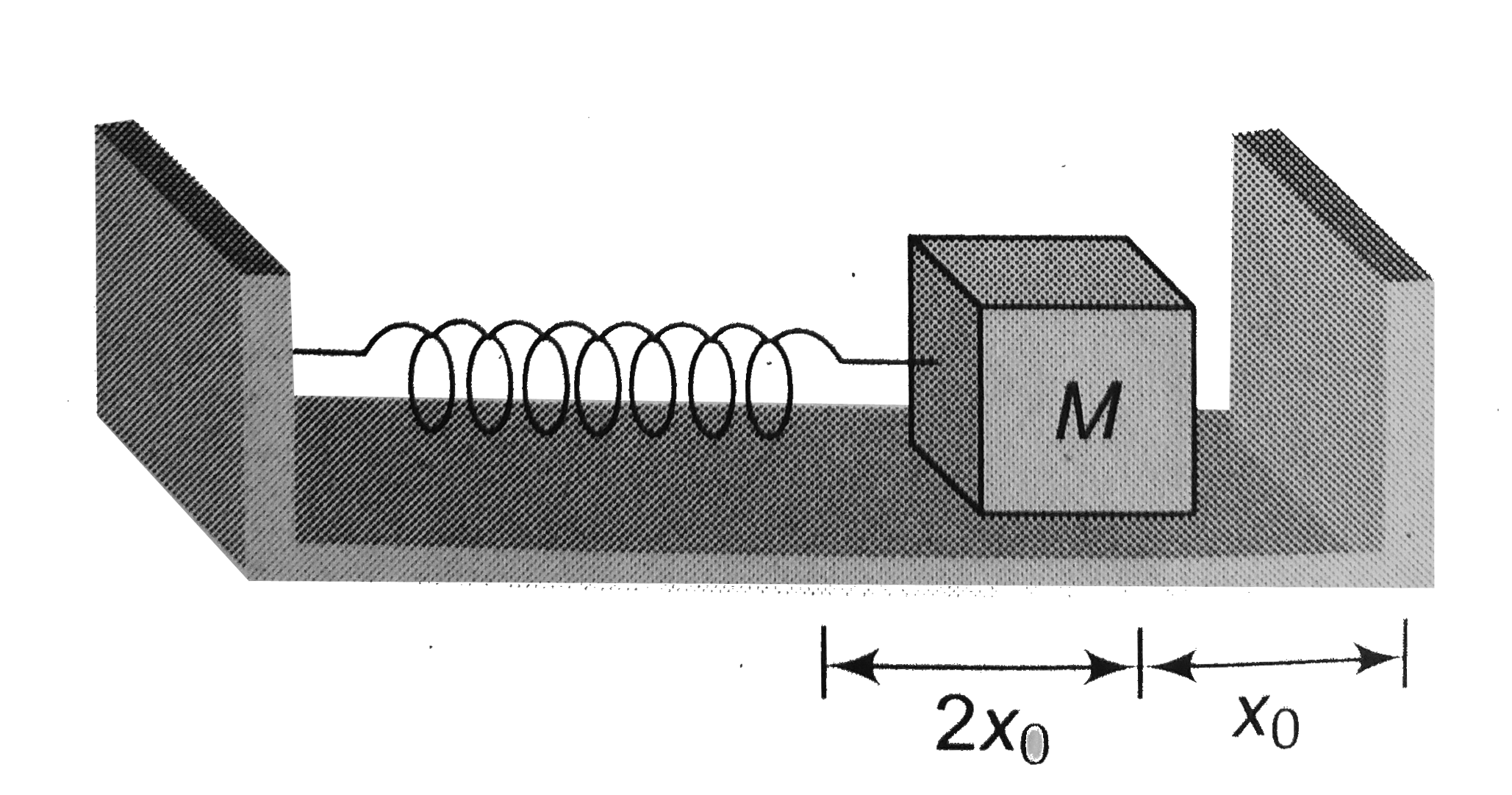
View SolutionA point mass m and charge q is connected with massless spring of natural length L. Initially spring is in its natural length. If a horizontal uniform electric field E is switched on as shown in figure, then the maximum separation between the point mass and the wall is: (Assume all surface are frictionless)

View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When thye spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

View Solution
