A block is released from point A as shown in figure .All surfaces are smooth and there is no loss of mechnical energy anywhere. Find the time period of oscillation of block.

The correct Answer is:A, B, C
As there is no loss of mechanical energy, the block rises upto the same height 'h' on other side also.
AB=hsinα'BC=hsinβ
a1=gsina, a2=gsinβ
uA=uC=0
Using t=√2sa
(with u=0)
:. Time period of oscillation,
T=2tAB+2tCB=2(tAB+tCB)
=2⎡⎢
⎢⎣
⎷2×hsinαgsinα+
⎷2×hsinβgsinβ⎤⎥
⎥⎦
=2√2hg[cosecα+cosecβ]

Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 7
1 Video
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 8
1 Video
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 5
7 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Knowledge Check
In the following figure all surfaces are smooth. The system is released from rest , then :
 Aacceleration of wedge is greater then gtanθBacceleration of m is g√1+2cos2θCacceleration of m is gDacceleration of wedge is gsinθ
Aacceleration of wedge is greater then gtanθBacceleration of m is g√1+2cos2θCacceleration of m is gDacceleration of wedge is gsinθThe right block in figure moces at a speed V towards the left block placed in equilibrium. All the surfaces are smooth and all the collisions are elastic. Find the time period motion. Neglect the width of the blocks.
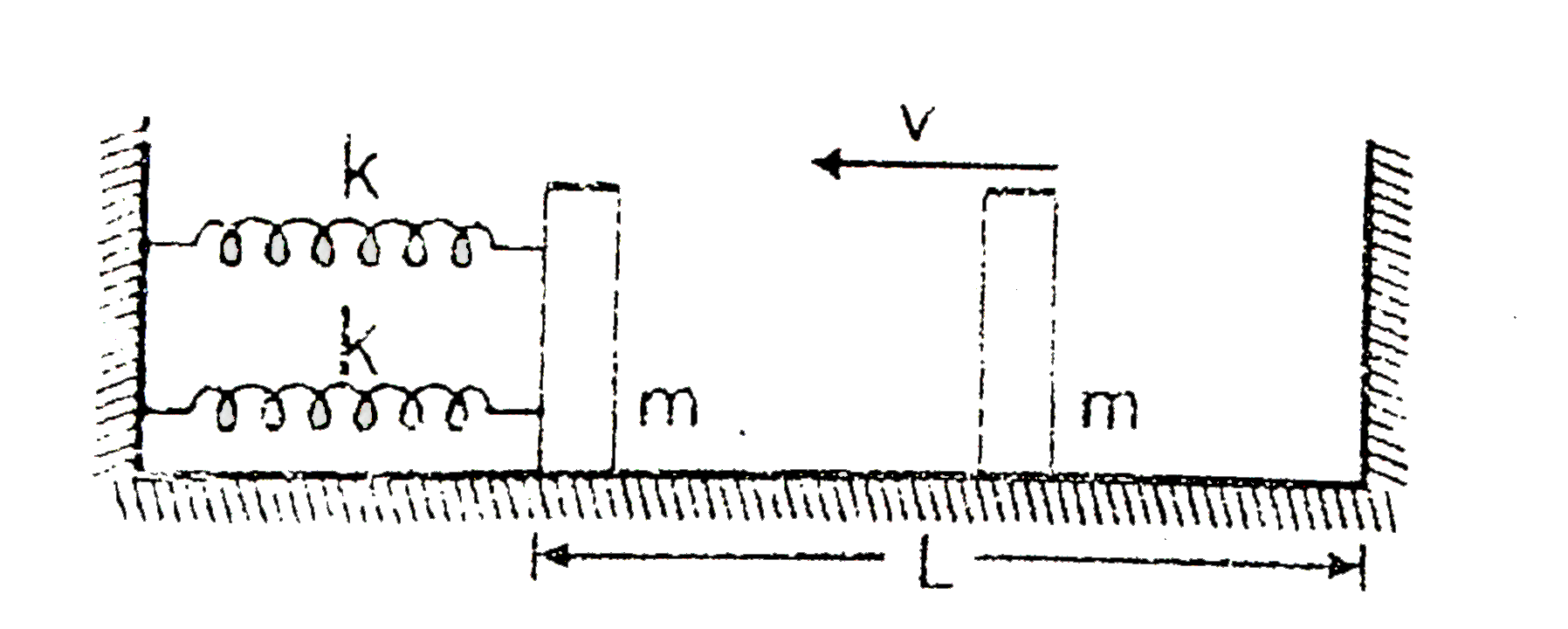 Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+LvThe right block in figure moces at a speed V towards the left block placed in equilibrium. All the surfaces are smooth and all the collisions are elastic. Find the time period motion. Neglect the width of the blocks.
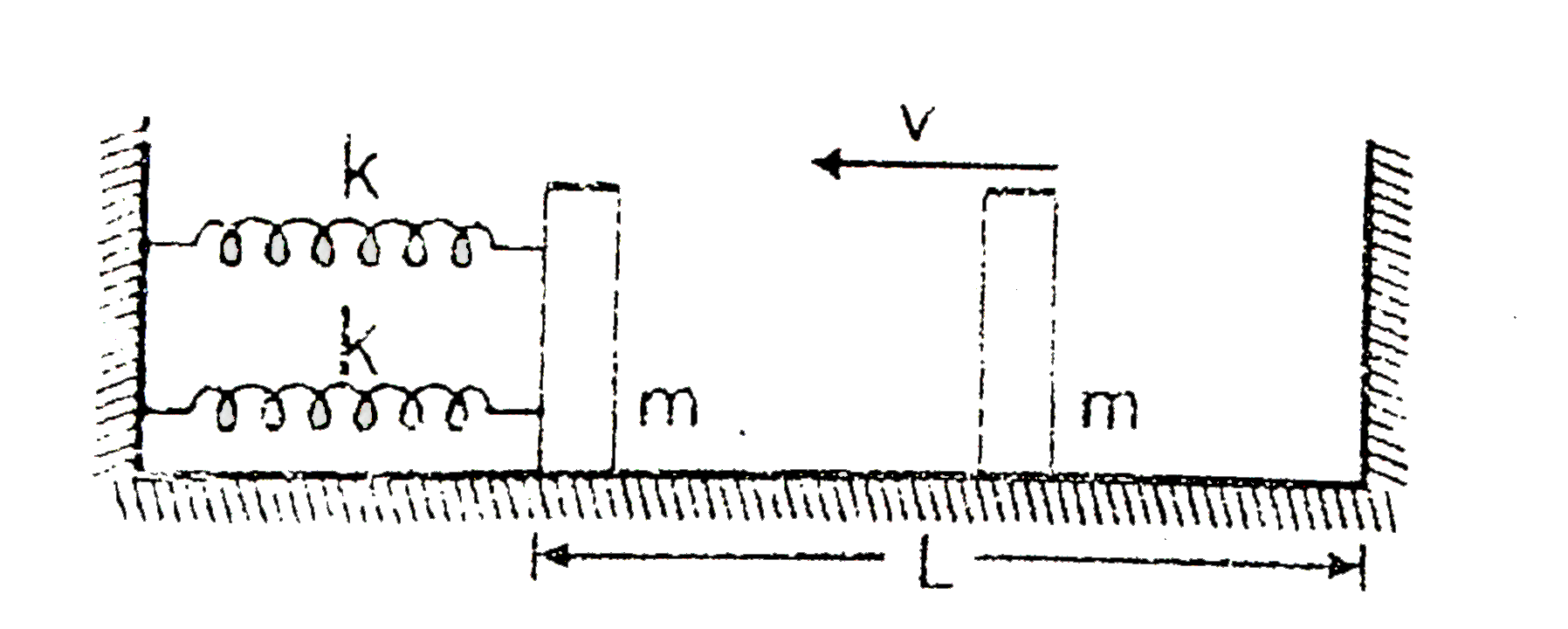 Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
A small block oscillates back and forth on a smooth concave surface of radius R. Find the time period of small oscillation.

View SolutionFigure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards loft so that spring is compressed by a distance 5l/3 and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.

View SolutionAn arrangement is shown in figure. If all the surfaces are smooth and system is released from rest then the relation between accelerations of blocks P(ap)andQ(a_Q) will be
View SolutionIn the device shown in the figure, the block of mass 20 kg is displaced down slighty and released, it starts oscillating. Pulleys are smooth and massless, strings and springs are also massless. Find the time period of oscillation (K1=4N/m,K2=4N/m)
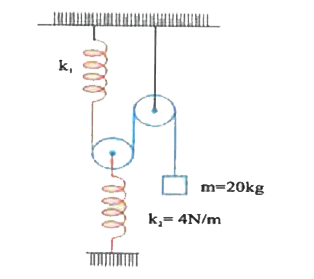
View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

View Solution