A block in SHM starts from +A position. Write S−t equation of the block, if S is measured from −A.
The correct Answer is:A, C
When the block starts from +A and x at any time 't' is measured from the mean position, then
x=Acosωt
In the figure, we can see that
S=A+xor S=A+Acosωt or S=A(1+cosωt)
Check From the equation we can see that,
S=2A at t=0
S=A at t=T4 and ω=2πT⇒ωt=π2
S=0 at T=T2 and ω=2πT⇒ωt=π .
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 9
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 10
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 7
1 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
S-Block
View SolutionA block is performin SHM of amplitude 'A' in vertical direction. When block i8s at 'y' (measured from mean position), it detaches froms spring, so that spring contracts and does not effect the motion of the block. Find 'y⋅' such that block attains maximum height from the mean position. (given Aω2>g)
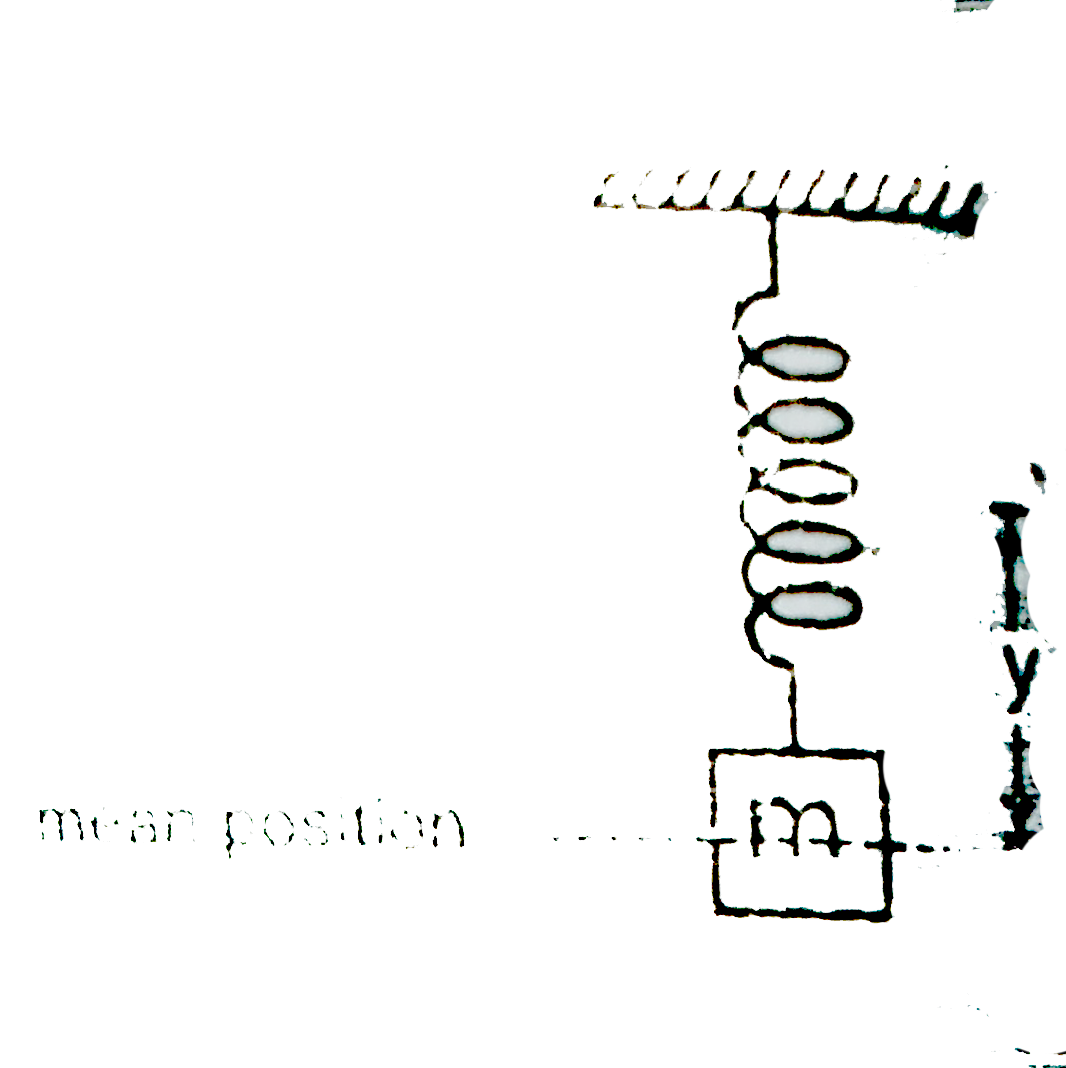
View Solution
Knowledge Check
If the particle in linear S.H.M. starts from the extreme left position, then its equation of motion is given by
Ax=Asin(ωt+π/2)Bx=Asin(ωt−π/2)Cx=−Asin(ωt+π/2)Dx=AcosωtA particle performing SHM starts from mean position. The phase of that particle is π/s when it has
Amaximum displacementBmaximum velocityCmaximum energyDmaximum kinetic energyThe friction force acting on the block at time t=4s will be
A50NB30NC25NDNone
A block is performin SHM of amplitude 'A' in vertical direction. When block i8s at 'y' (measured from mean position), it detaches froms spring, so that spring contracts and does not effect the motion of the block. Find 'y⋅' such that block attains maximum height from the mean position. (given Aω2>g)
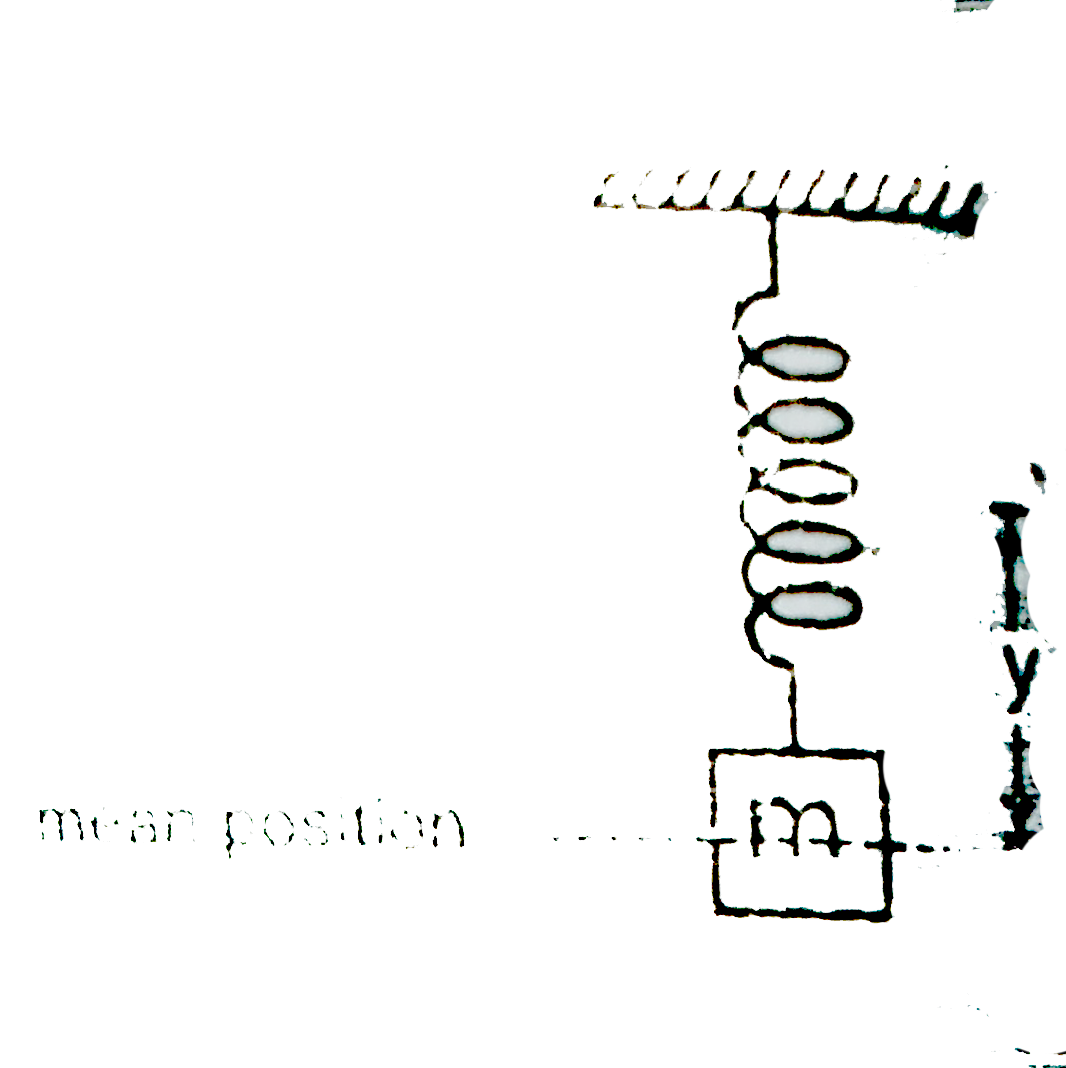
View SolutionA spring block system is kept inside the smooth surface of a trolley as shown in finger.
At t=0 trolley is given an acceleration 'a' in the direction shown in figure. Write S−t equation of the block
(a) with respect to trolley.
(b) with respect to ground.
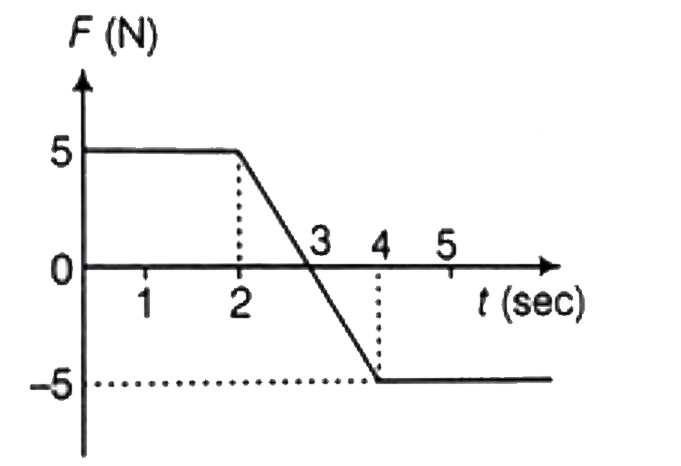
View SolutionA block of the mass of 1 kg is moving on the x -axis. A force F acting on the block is shown. The veloity of the block at time t = 2 s is −3ms−1. What is the speed of the block at time t = 4 s?
View SolutionA 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_052_Q01.png)
Let us now make a slight change to the initial conditions. At t=0, let the block be released from the same position with an initial velocity v1=64cm/s. Position of the block as a function of time can be expressed as
View SolutionThe periodic time of a particle performing a linear S.H.M. is 12 sec. It starts from the mean position. After 2 seconds, its velocity is found to be πcm/sec. What is the amplitude of S.H.M. ?
View Solution