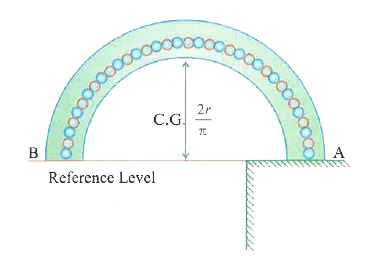
A uniform chain of length of length πr lies inside a smooth semicircular tube (AB) of radius f. Assuming a slight disturbance to start the chain in motion, the velocity it will emerge from the end (B) of the tube will be

√gr(1+29π)
√2gr(2π+π2π)
√gr(π+2)
√πgr
The correct Answer is:B
dm=(mπ)dθ

∴dU=(dm)gh=(mπdθ)grsinθ
Ui=∫π0dU=2mgrπ
Now, Ki+Ui=Kf+Uf
∴0+2mgrπ=12mv2−mg(πr2)
∴v=√2gr(2π+π2).
Similar Questions
A uniform chain of length l and mass m lies on a smooth table. A very small part of this chain hangs from the table. It begins to fall under the weight of hanging part. Find the velocity of chain when the length of hanging part becomes y.
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration of the each element of the chain when its upper end is released? It is assumed that the length of the chain l<(πR2).
View Solution
Knowledge Check
A heavy flexible uniform chain of length πr and mass λπr lies in a smooth semicircular tube AB of radius 'r'. Assuming a slight disturbane to start the chain in motion, find the velocity v with which it will emerge from the end of the tube?
 A√2π+π2B√2rg(2π+π2)C√2rg(1π+π)D√rf(π+2π)
A√2π+π2B√2rg(2π+π2)C√2rg(1π+π)D√rf(π+2π)A smooth semicircular tube AB of radius r is fixed in a vertical plane and contains a heavy flexible chain of length πr and weight Wπr as shown. Assuming a slight disturbance to start the chain in motion, the velocity v with it will emerge from the open end B of the tube is:
 A4grπB2grπC√2gr(2π+π)D√2gr(2π+π2)
A4grπB2grπC√2gr(2π+π)D√2gr(2π+π2)A uniform chain of length l is placed on a smooth horizontal table, such that half of its length hangs over one edge. It is releasedfrom rest, the velocity with which it leaves the table is
A√3gl4B√3gl2C√2gl3D√gl3
A uniform chain of mass m and length l<πR2 is placed on a smooth hemisphere of radius R with on of its ends fixed at the top of the sphere.
(a) Find the gravitational potential energy of chain assuming base of hemisphere as reference.
(b) what will be the tangential acceleraion of the chain when it starts sliding down.
(c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle β.
View SolutionA uniform chain of mass m and length l is placed on a smooth table so that one−third length hanges freely as shown in the figure. Now the chain is released, with what velocity chain slips off the table?

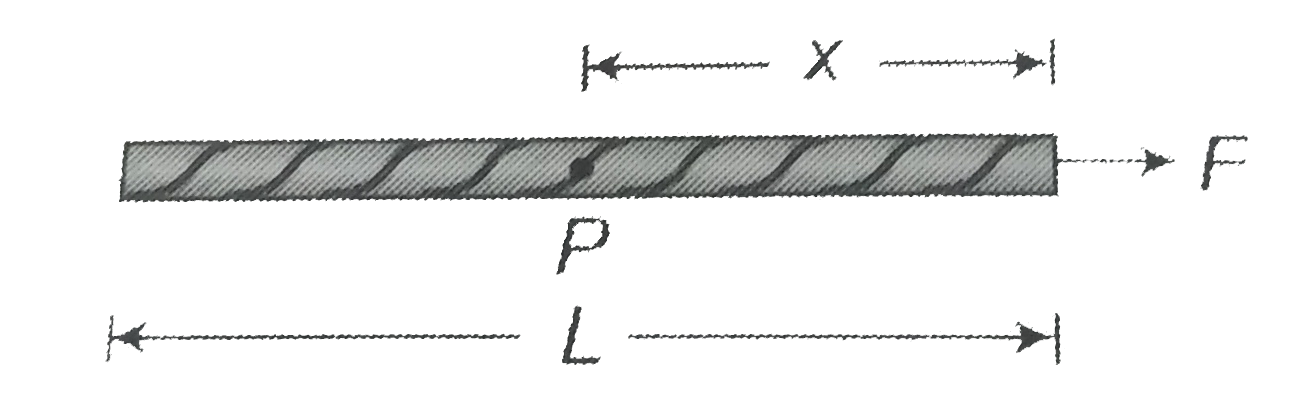
View SolutionA uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
View SolutionA chain AB of length l is located in a smooth horizontal tube so that its fraction of length h hangs freely and touches the surface of the table with its end B(figure). At a certain moment the end A of the chain is set free. With what velocity will this end of the chain slip out of the tube?

View SolutionA uniform chain of length L lies on a smooth horizontal table with its length perpendicular to the edge of the table and a small portion of the chain is hanging over the edge. The chain starts sliding due to the weight of the hanging part
View Solution
