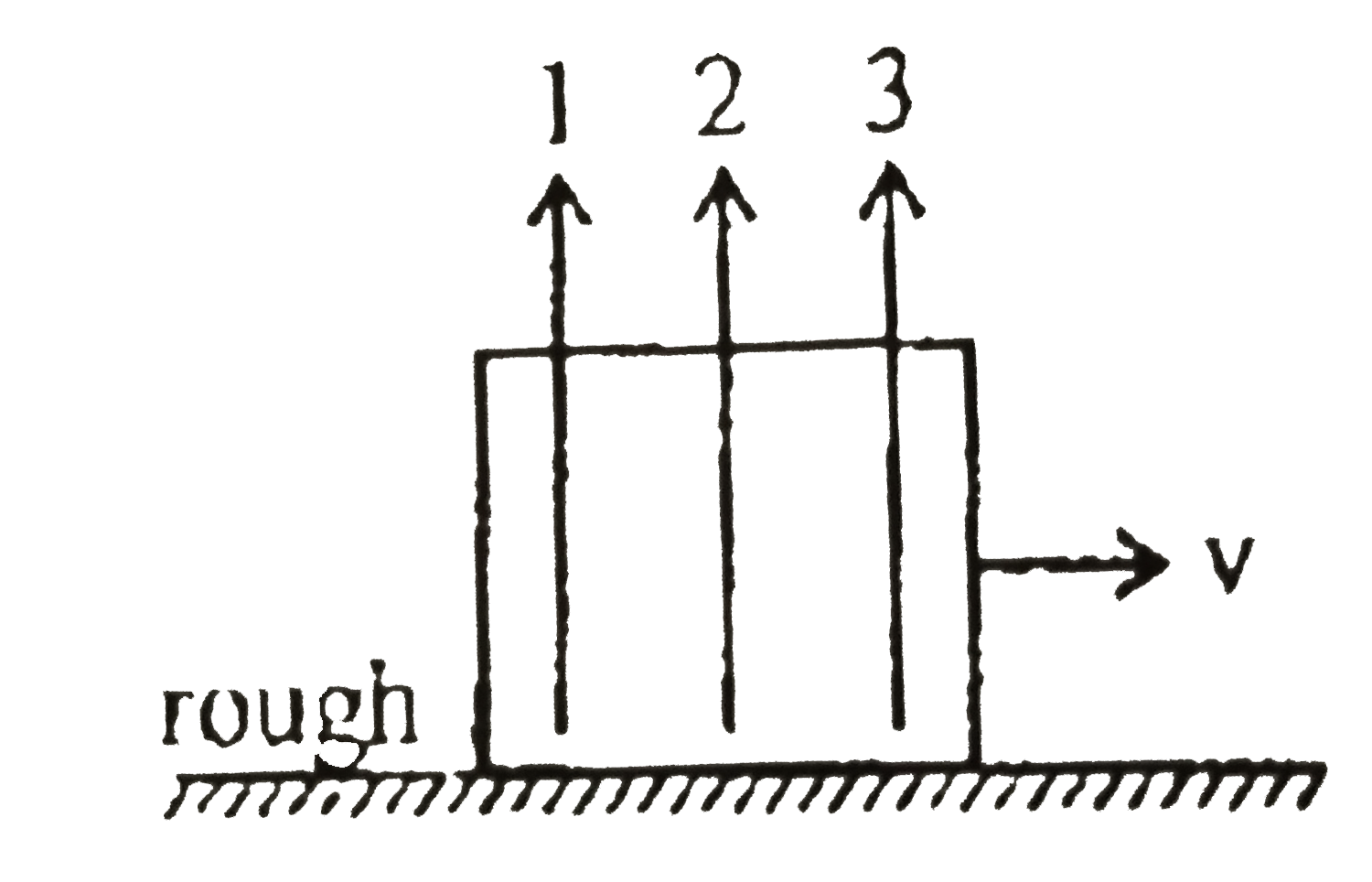
A horizontal force F=mg3 is applied on the upper surface of a uniform cube of mass m and slide a which is resting on a rough horizontal surface having μ=12. The distance between lines of action of mg and normal reation is
a2
a3
a4
None of these
The correct Answer is:B
To solve the problem step by step, we need to analyze the forces acting on the cube and the moments about a point.
1. Identify the Forces Acting on the Cube:
- The weight of the cube, mg, acts downward at the center of the cube.
- The normal force N acts upward at the base of the cube.
- A horizontal force F=mg3 is applied at the top of the cube.
- There is a frictional force f opposing the applied force, which will also be equal to F since the cube is at rest (static equilibrium).
2. Equilibrium Conditions:
- Since the cube is at rest, the net force in both horizontal and vertical directions must be zero.
- In the vertical direction:
N=mg
- In the horizontal direction:
f=F=mg3
3. Determine the Moments about the Center of the Cube:
- Let's denote the center of the cube as point C.
- The distance from the center C to the line of action of the weight mg is 0 (since it acts at the center).
- The distance from the center C to the line of action of the normal force N is x (which we need to find).
- The distance from the center C to the line of action of the applied force F is A2 (where A is the side length of the cube).
4. Setting Up the Moment Equation:
- The moments about point C must sum to zero:
Clockwise moments=Counterclockwise moments
- The friction force f creates a clockwise moment:
f⋅A2=mg3⋅A2
- The normal force N creates a counterclockwise moment:
N⋅x=mg⋅x
5. Equating the Moments:
- The equation becomes:
mg3⋅A2=mg⋅x
- Simplifying this, we can cancel mg from both sides (since mg≠0):
13⋅A2=x
- Thus, we find:
x=A6
6. Finding the Distance Between Lines of Action:
- The distance between the lines of action of mg and N is x.
- Therefore, the distance is:
x=A3
Final Answer:
The distance between the lines of action of mg and the normal reaction N is A3.
- The weight of the cube, mg, acts downward at the center of the cube.
- The normal force N acts upward at the base of the cube.
- A horizontal force F=mg3 is applied at the top of the cube.
- There is a frictional force f opposing the applied force, which will also be equal to F since the cube is at rest (static equilibrium).
- Since the cube is at rest, the net force in both horizontal and vertical directions must be zero.
- In the vertical direction:
N=mg
- In the horizontal direction:
f=F=mg3
- Let's denote the center of the cube as point C.
- The distance from the center C to the line of action of the weight mg is 0 (since it acts at the center).
- The distance from the center C to the line of action of the normal force N is x (which we need to find).
- The distance from the center C to the line of action of the applied force F is A2 (where A is the side length of the cube).
- The moments about point C must sum to zero:
Clockwise moments=Counterclockwise moments
- The friction force f creates a clockwise moment:
f⋅A2=mg3⋅A2
- The normal force N creates a counterclockwise moment:
N⋅x=mg⋅x
- The equation becomes:
mg3⋅A2=mg⋅x
- Simplifying this, we can cancel mg from both sides (since mg≠0):
13⋅A2=x
- Thus, we find:
x=A6
- The distance between the lines of action of mg and N is x.
- Therefore, the distance is:
x=A3
The distance between the lines of action of mg and the normal reaction N is A3.
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Exercise 8.5
Explore 2 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A force (F = Mg) is applied on the top of a circular ring ofmass M and radius R keot on a rough horizontal surface. If the ring rolls without slipping, the minimum coefficient of friction required is
_PHY_214_Q01.png)
View SolutionA uniform cubical block is sliding on rough surface as shown. Find possible line of action of normal reaction acting on the block due to rough horizontal surface.
View Solution
Knowledge Check
A horizontal force F=mg/3 is applied on the surface of a uniform cube of mass 'm' and side 'a' which is resting on a rough horizontal surface having μS=1/2. The distance between lines of action of 'mg' and normal reactiom 'N' is -
Aa/2Ba/3Ca/4DNoneA uniform cube of mass m and slidea is resting in equilibrium on a rough 45∘ inclined surface. The distance point of application of normal reation measured from the lower edge of the cube is
AzeroBa3Ca√2Da4A block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNone
Time varying force horizontal F=K0t is applied on a block of mass placed at rest on a rough horizontal surface ( μ is coefficient of friction).At a time t=3μmgK0 the acceleration of the block is given by a=pμg where p=...........(K0is a positive constant)
View SolutionIf F is the force applied , then acceleration of the body of mass M when body is on rough horizontal surface
View SolutionA body of mass m, having momentum p, is moving on a rough horizontal surface. If it is stopped in a distance x, the coefficient of friction between the body and the surface is given by
View SolutionA block of mass m is pulled slowly by a minimum constant force on a rough (μ) horizontal surface through a distance x. Find work done by force F.
View SolutionA horizontal force of 20 N is applied to a block of 10 kg resting on a rough horizontal surface. How much additional force is required to just move the block, if the coefficient of static friction between the block and the surface is 0.4 ?
View Solution

