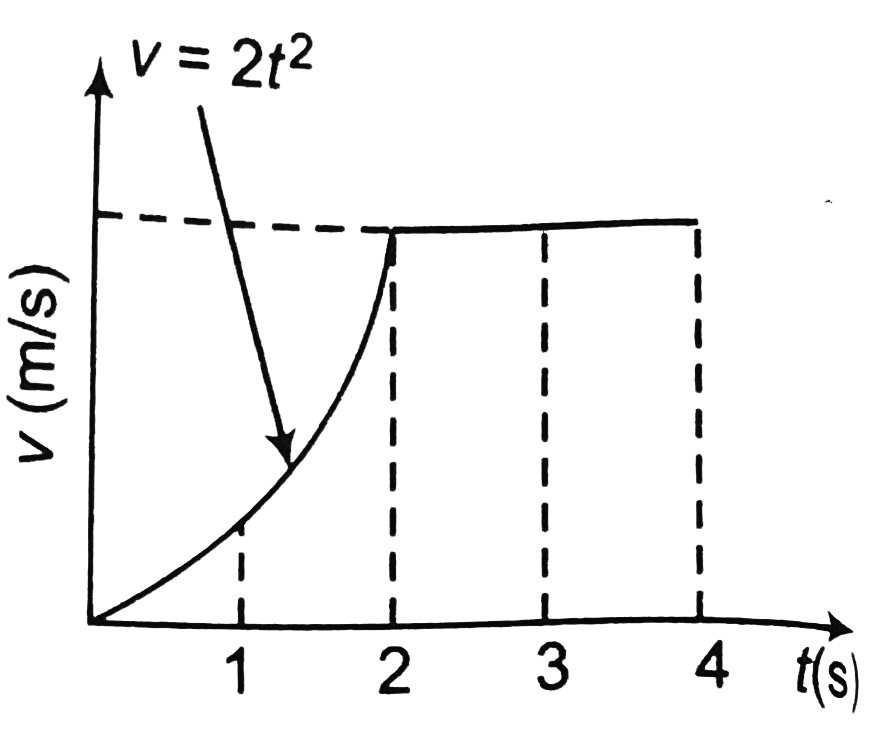
A car begains from rest at time t=0, and then acceleration along a straight track during the interval 0<t≤2s and thereafter with constant velocity as shown in figure in the graph. A coin is initially at rest on the floor of the car. At t=1s, the coin begains to slip and its stops slipping at t=3s . The coefficient of static friction between the floor and the coin is (g=10m/s2)
0.2
0.3
0.4
0.5
The correct Answer is:C
v=2t2
∴a=dvdt=4t At t=1s,
a=4m/s2 …(i)
Limiting value of static friction ,
fL=μSmg
∴ Maximum value of acceleration of coin which can be provided by the friction ,
amax=fLm=μSmg
Equating Eqs. (i) and (ii), we get
4=μS(10)
μS=0.4
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.5
2 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A car starts from rest at time t = 0 and it a-t graph is shown in figure. A coin is initially at rest on the floor of the car. At t = 1 s the coin begins to slip and it stops slipping at t = 3 s. The coefficient of static friction between the floor and the coin is (g = 10 m/s2)
_PHY_E05_188_Q02.png)
View SolutionA long plank begins to move at t=0 and accelerates along a straight track wit a speed given by v=2t2 for 0≤t≤2 (where v is in m/s and t is in second). After 2 sec the plane continues to move at the constant speed acquired. A small initially at rest on the plank begins to slip at t=1 sec and stops sliding at t=3 sec. If the coefficient of static friction and kinetic friction between the plank and the block is 0.s and 0.k (where s and k are digits) respectively, find s+k (take g=10m/s2)
View Solution
Knowledge Check
The velocity-time plot is shown in figure. Find the average speed in time interval t=0 to t=40s during the period.
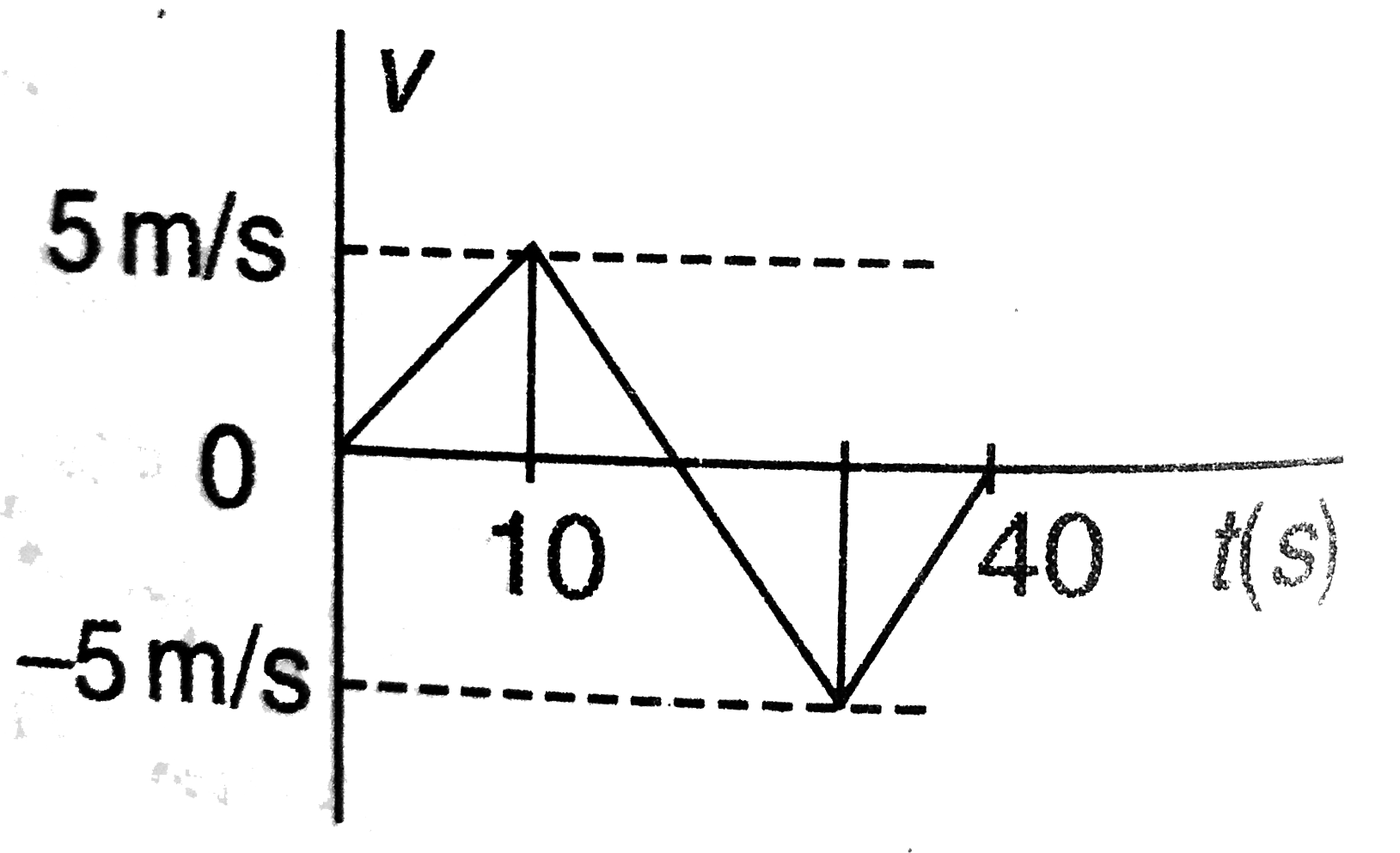AzeroB2.5m/sC5m/sDnoneA car starts from rest and moves with uniform acceleration a on a straight road from time t=0 to t=T. After that, a constant deceleration brings it to rest. In this process the average speed of the car is
AaT4B3aT2CaT2DaTA body starts from rest at time t=0 , the acceleration time graph is shown in the figure . The maximum velocity attained by the body will be
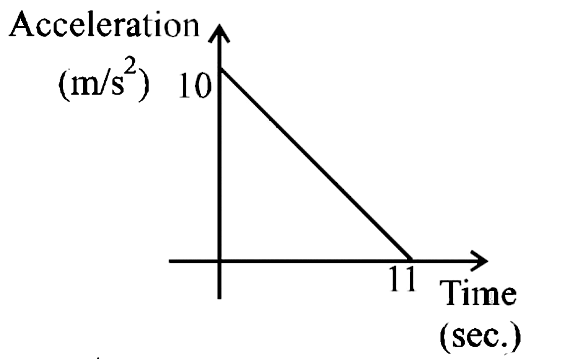A110m/sB55m/sC650m/s(a)D550m/s
A long plank begins to move at t=0 and accelerates along a straight track wit a speed given by v=2t2 for 0≤t≤2 (where v is in m/s and t is in second). After 2 sec the plane continues to move at the constant speed acquired. A small initially at rest on the plank begins to slip at t=1 sec and stops sliding at t=3 sec. If the coefficient of static friction and kinetic friction between the plank and the block is 0.s and 0.k (where s and k are digits) respectively, find s+k (take g=10m/s2)
View SolutionA car accelerates from rest with 2ms−2 for 2s and then decelerates constantly with 4ms−2 for t0 second to come to rest. The graph for the motion is shown in figure.
a. Find the maximum speed attained by the car.
b. Find the value of t0.
View SolutionAn experimental car in fig (a) starts from rest and travels along a straight track such that it accelerates at a constant rate for 10 s and then decelerates at a constant rate draw the v-t and s-t graphs and determine the time t' needed to stop the car. how far has the car travelled.?
View SolutionA particle starts from rest and moves with a constant acceleration along a straight path to attain 64 m s−1 in t s. If at t = (t + 3)s the speed is 76 ms−1, then find the acceleration of the particle and 't'.
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
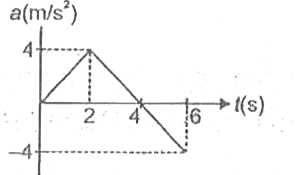
View Solution