If F is the force applied , then acceleration of the body of mass M when body is on rough horizontal surface
fkM
F−fkM
FM
None of these
The correct Answer is:B
To find the acceleration of a body of mass M on a rough horizontal surface when a force F is applied, we can follow these steps:
Step 1: Identify the forces acting on the body
When a force F is applied to the body on a rough surface, two main forces are acting on it:
- The applied force F (in the direction of motion)
- The frictional force Fk (acting in the opposite direction to the applied force)
Step 2: Determine the type of friction
Since the body is moving, we will consider kinetic friction. The kinetic friction force Fk can be calculated using the formula:
Fk=μk⋅N
where μk is the coefficient of kinetic friction and N is the normal force. On a horizontal surface, the normal force N is equal to the weight of the body, which is M⋅g (where g is the acceleration due to gravity).
Thus, we have:
Fk=μk⋅(M⋅g)
Step 3: Apply Newton's second law of motion
According to Newton's second law, the net force acting on the body is equal to the mass of the body multiplied by its acceleration a:
Fnet=M⋅a
The net force Fnet can be expressed as the difference between the applied force and the frictional force:
Fnet=F−Fk
Step 4: Set up the equation
Combining the equations from Steps 2 and 3, we can write:
F−Fk=M⋅a
Substituting for Fk:
F−μk⋅(M⋅g)=M⋅a
Step 5: Solve for acceleration a
Rearranging the equation to solve for acceleration a:
a=F−μk⋅(M⋅g)M
Final Result
Thus, the acceleration a of the body of mass M on a rough horizontal surface when a force F is applied is given by:
a=F−μk⋅(M⋅g)M
When a force F is applied to the body on a rough surface, two main forces are acting on it:
- The applied force F (in the direction of motion)
- The frictional force Fk (acting in the opposite direction to the applied force)
Since the body is moving, we will consider kinetic friction. The kinetic friction force Fk can be calculated using the formula:
Fk=μk⋅N
where μk is the coefficient of kinetic friction and N is the normal force. On a horizontal surface, the normal force N is equal to the weight of the body, which is M⋅g (where g is the acceleration due to gravity).
Fk=μk⋅(M⋅g)
According to Newton's second law, the net force acting on the body is equal to the mass of the body multiplied by its acceleration a:
Fnet=M⋅a
The net force Fnet can be expressed as the difference between the applied force and the frictional force:
Fnet=F−Fk
Combining the equations from Steps 2 and 3, we can write:
F−Fk=M⋅a
Substituting for Fk:
F−μk⋅(M⋅g)=M⋅a
Rearranging the equation to solve for acceleration a:
a=F−μk⋅(M⋅g)M
Thus, the acceleration a of the body of mass M on a rough horizontal surface when a force F is applied is given by:
a=F−μk⋅(M⋅g)M
Similar Questions
A tangential force 'F' is applied at the topmost point of a spherical shell of mass 'm' kept on a rough horizontal surface. If it rolls without slipping, it's acceleration is 6Fxm then 'x'
View SolutionAt the instant t=0, a force F=kt (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is
View Solution
Knowledge Check
A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 AF2 towards rightBF3 towards leftC2F3 towards rightDZero
AF2 towards rightBF3 towards leftC2F3 towards rightDZeroA body kept on a smooth horizontal surface is pulled by a constant horizontal force applied at the top point of the body. If the body rolls purely on the surface, its shape can be-
Athin pipeBuniform cylinderCuniform sphereDthin spherical shellA constant force of 20N is applied to pull a body of mass 10 k, kept on a smooth horizontal surface. What is the increase in its kinetic energy if the body starts from rest and covers a distance of 5m?
A100JB150JC80JD60J
A force of 19.6 N when applied parallel to the surface just moves a body of mass 10 kg kept on a horizontal surface. If a 5 kg mass is kept on the first mass, the orce applied parallel to the surface to just move the combined body is
View SolutionA plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank

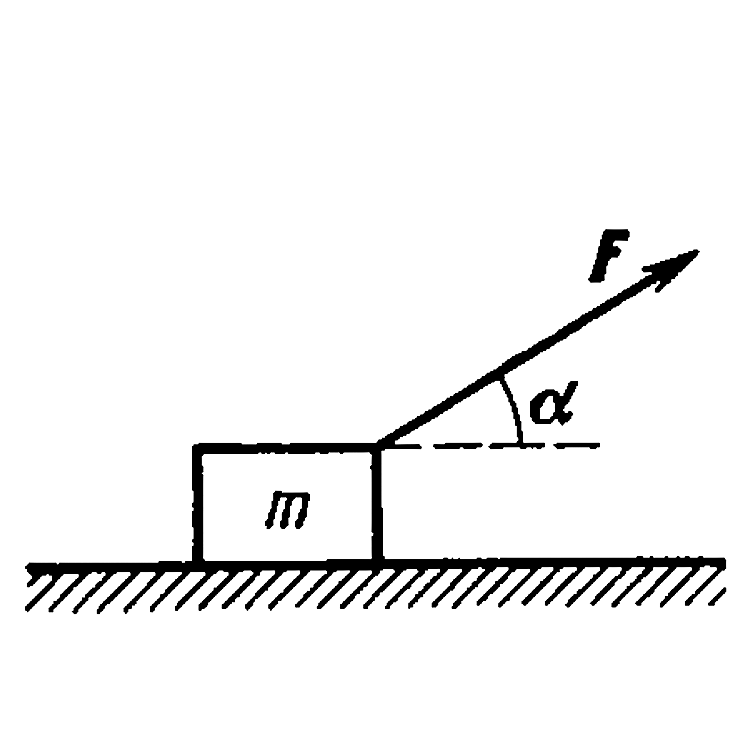
View SolutionAt the moment t=0 the force F=at is applied to a small body of mass m resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle α with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
View SolutionA body of mass 8kg lies on a rough horizontal table. It is observed that a certain horizontal force gives the body an acceleration of the body is 16ms−2 . The coefficient of friction is.
View SolutionA body of mass M is applying horizontal force to slide a box of mass M1 on a rough horizontal surface The coefficient of friction between the shoe of the boy and the floor is μ and that between the box and the floor is 'μ1' In which of the following cases is it certainly not possible to slide the box ? .
View Solution

