A horizontal force of 20 N is applied to a block of 10 kg resting on a rough horizontal surface. How much additional force is required to just move the block, if the coefficient of static friction between the block and the surface is 0.4 ?
15.5 N
10.3 N
8.5 N
19.2 N
The correct Answer is:D
To solve the problem, we need to determine how much additional force is required to just move a block resting on a rough horizontal surface when a horizontal force of 20 N is already applied. The coefficient of static friction between the block and the surface is given as 0.4.
Step 1: Calculate the weight of the block.
The weight (W) of the block can be calculated using the formula:
W=m⋅g
where:
- m=10kg (mass of the block)
- g=9.8m/s2 (acceleration due to gravity)
Calculating the weight:
W=10kg⋅9.8m/s2=98N
Step 2: Calculate the normal force (N).
On a horizontal surface, the normal force is equal to the weight of the block:
N=W=98N
Step 3: Calculate the maximum static friction force (Fs).
The maximum static friction force can be calculated using the formula:
Fs=μ⋅N
where:
- μ=0.4 (coefficient of static friction)
Calculating the static friction force:
Fs=0.4⋅98N=39.2N
Step 4: Determine the total force required to overcome static friction.
To just move the block, the total applied force must equal the static friction force. The total force (F_total) applied is the sum of the already applied force (F1) and the additional force (F2):
Ftotal=F1+F2
Given that F1=20N:
Ftotal=20N+F2
Setting this equal to the static friction force:
20N+F2=39.2N
Step 5: Solve for the additional force (F2).
Rearranging the equation to find F2:
F2=39.2N−20N=19.2N
Final Answer:
The additional force required to just move the block is 19.2 N.
---
The weight (W) of the block can be calculated using the formula:
W=m⋅g
where:
- m=10kg (mass of the block)
- g=9.8m/s2 (acceleration due to gravity)
W=10kg⋅9.8m/s2=98N
On a horizontal surface, the normal force is equal to the weight of the block:
N=W=98N
The maximum static friction force can be calculated using the formula:
Fs=μ⋅N
where:
- μ=0.4 (coefficient of static friction)
Fs=0.4⋅98N=39.2N
To just move the block, the total applied force must equal the static friction force. The total force (F_total) applied is the sum of the already applied force (F1) and the additional force (F2):
Ftotal=F1+F2
Ftotal=20N+F2
20N+F2=39.2N
Rearranging the equation to find F2:
F2=39.2N−20N=19.2N
The additional force required to just move the block is 19.2 N.
Topper's Solved these Questions
- FRICTIONAL IN SOLIDS AND LIQUIDS Book:MARVEL PUBLICATIONChapter:FRICTIONAL IN SOLIDS AND LIQUIDS Exercise:TEST YOUR GRASP
Explore 10 Videos
- FORCE, WORK AND TORQUEBook:MARVEL PUBLICATIONChapter:FORCE, WORK AND TORQUEExercise:TEST YOUR GRASP
Explore 10 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT Book:MARVEL PUBLICATIONChapter:MAGNETIC EFFECT OF ELECTRIC CURRENT Exercise:TEST YOUR GRASP
Explore 10 Videos
Similar Questions
A block of weight 200N is pulled along a rough horizontal surface at contant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is .
View SolutionA block of mass 4 kg is resting on a horizontal table and a force of 10 N is applied on it in the horizontal direction. The coefficient of kinetic friction between the block and the table is 0.1. The work done in √20 s
View Solution
Knowledge Check
A block of 50 kg rests on a table. A horizontal force of 294 N is required to just move the block, the coefficient of static friction between the surfaces in contant (μs) is
A5.88B1.67C0.6D0.17A wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
AFM(cosϕ+μsinϕ)−μgBFsin(ϕ)MCμFcosϕD,uFsinϕA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
A0.25B1√2C√2D1
A homogenous block of mass m, width b and height h is resting on a rough horizontal surface A horizontal force F is applied to it , which makes it to move with a constant velocity . The coefficient of friction between block and surface is μ Find the greatest height at which force F may be applied to slide the block with out tipping over
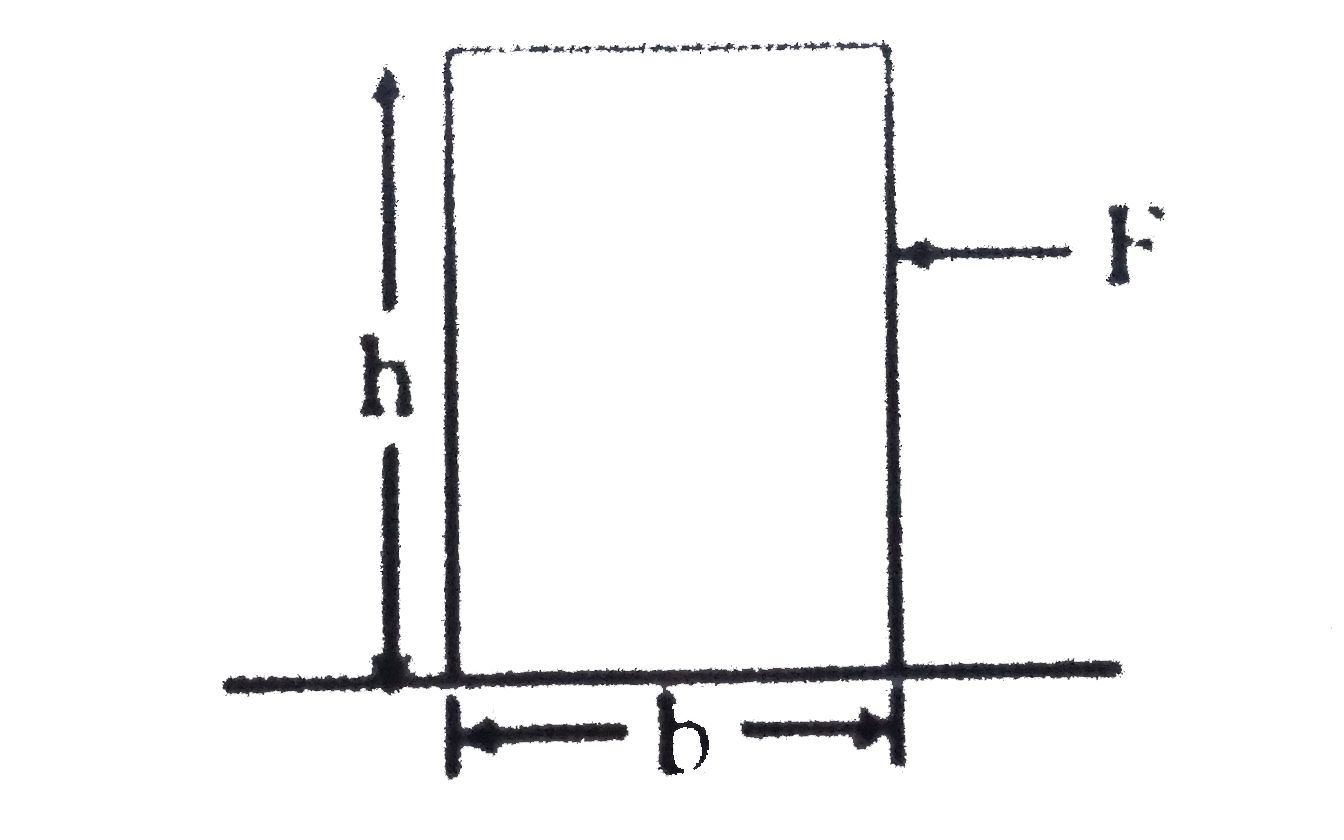
View SolutionA block of weight 200N is pulled along a rough horizontal surface at constant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is
View SolutionA force of 49 N just able to move a block of wood weighing 10 kg on a rough horizontal surface , then coefficient of friction is
View SolutionA horizontal force of 20 N i sapplied to a block of mass 4 kg resting on a rough horiozontal table. If the blcok does not move on the table, how much fricrtional force the table is applying on the blockgt What can be said about the coefficient of static friction between the block and the table? Takeg=ms2.
View SolutionA block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
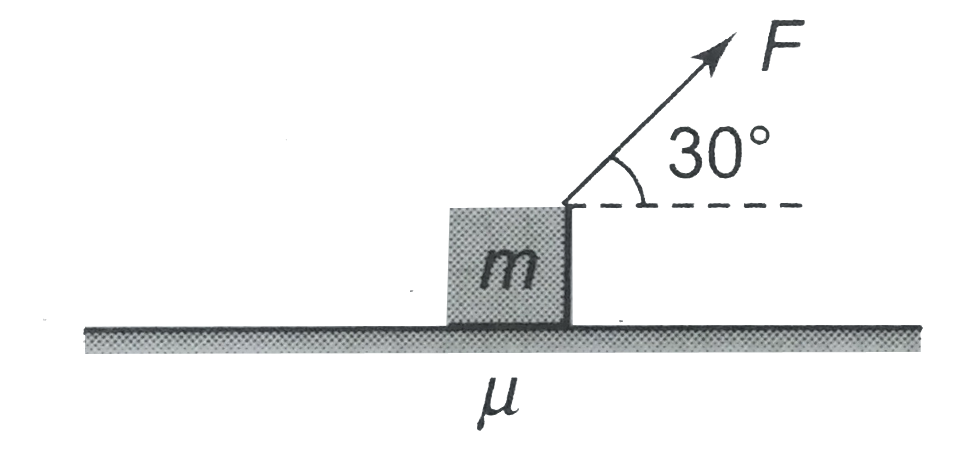
View Solution

