ABCD एक समांतर चतुर्भुज है जिसके विकर्ण O पर प्रतिच्छेद करते है। यदि BO पर कोई बिंदु P हो तो सिद्ध कीजिए कि :
(i)ar(ΔADO)=ar(ΔCDO) (ii)ar(ΔABP)=ar(ΔCBP)
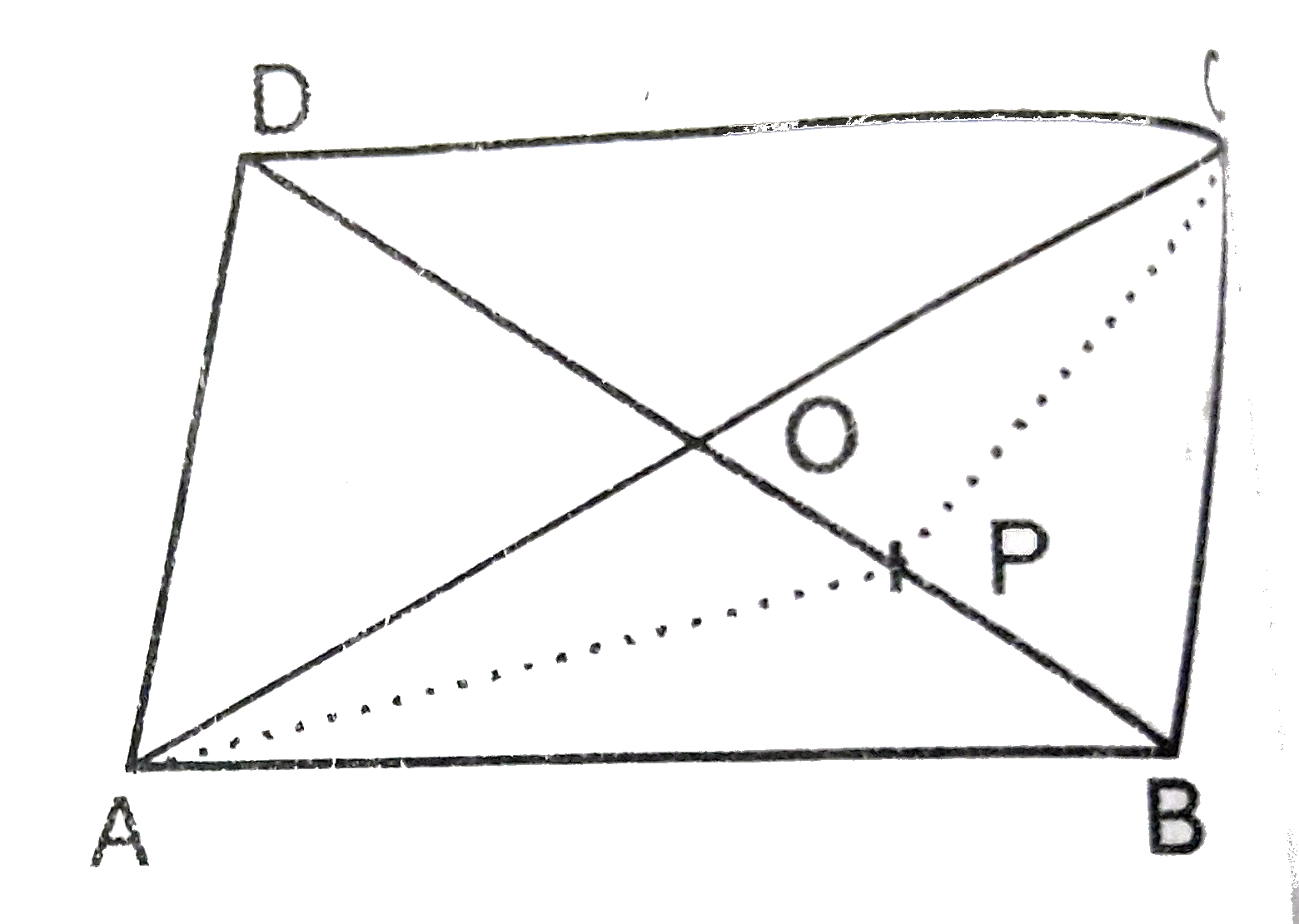
(i) चूँकि किसी समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते है अतः O , AC और BD का मध्य बिंदु है ।
ΔACD में, DO माध्यिका है।
∴ar(ΔADO)=ar(ΔCDO)
(ii) चूँकि O , AC का मध्यबिंदु है। अतः OP तथा OB क्रमशः त्रिभुज APC और ABC की माध्यिकाएँ है।
∴ar(ΔAOP)=ar(ΔCOP) और ar(ΔAOB)=ar(ΔCOB)
⇒ar(ΔAOB)−ar(ΔAOP)=ar(ΔCOB)−ar(ΔCOP)
⇒ar(ΔABP)=ar(ΔCBP)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:अति लघुत्तरात्मक प्रश्न
Explore 9 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:बहु विकल्पीय प्रश्न
Explore 20 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 15.2
Explore 4 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण Book:RD SHARMAChapter:संख्यिकीय आंकड़ों का आलेखीय निरूपण Exercise:बहु विकल्पीय प्रश्न
Explore 8 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:बहु विकल्पीय प्रश्न
Explore 17 Videos
Similar Questions
यदि ABC व BDE दो समबाहु त्रिभुज इस प्रकार है कि बिंदु D भुजा BC का मध्य बिंदु है, तो त्रिभुज ABC और त्रिभुज BDE के क्षेत्रफल का अनुपात ज्ञात करो।
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है। AE⊥DC तथा CF⊥AD । यदि AB = 16 सेमी, AE = 8 सेमी तथा CF = 10 सेमी , तो AD का मान ज्ञात कीजिये ।
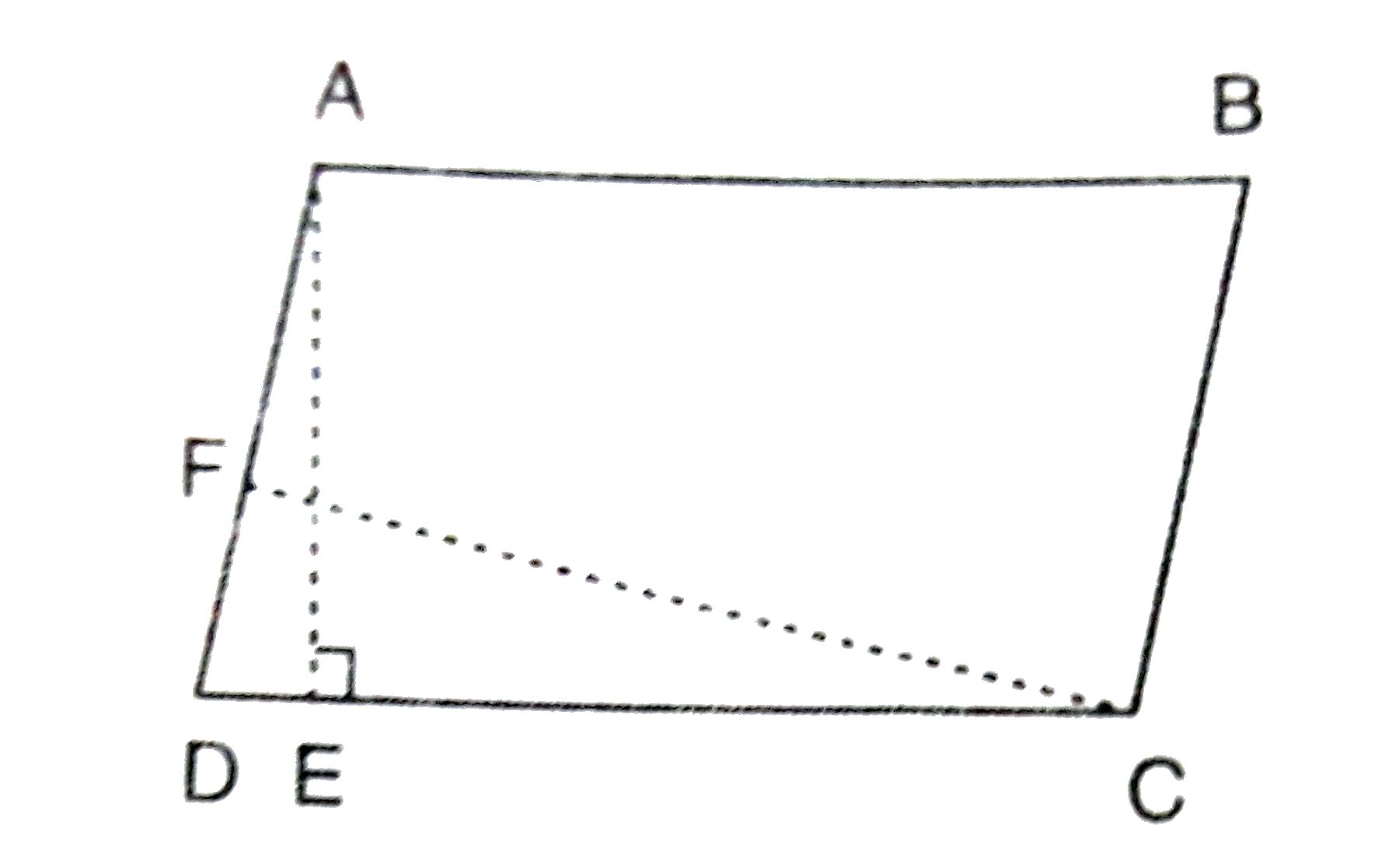
View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
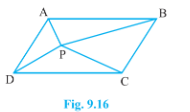
View Solutionआकृति में में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(APB)+ar(PCD)=12ar(ABCD)
(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
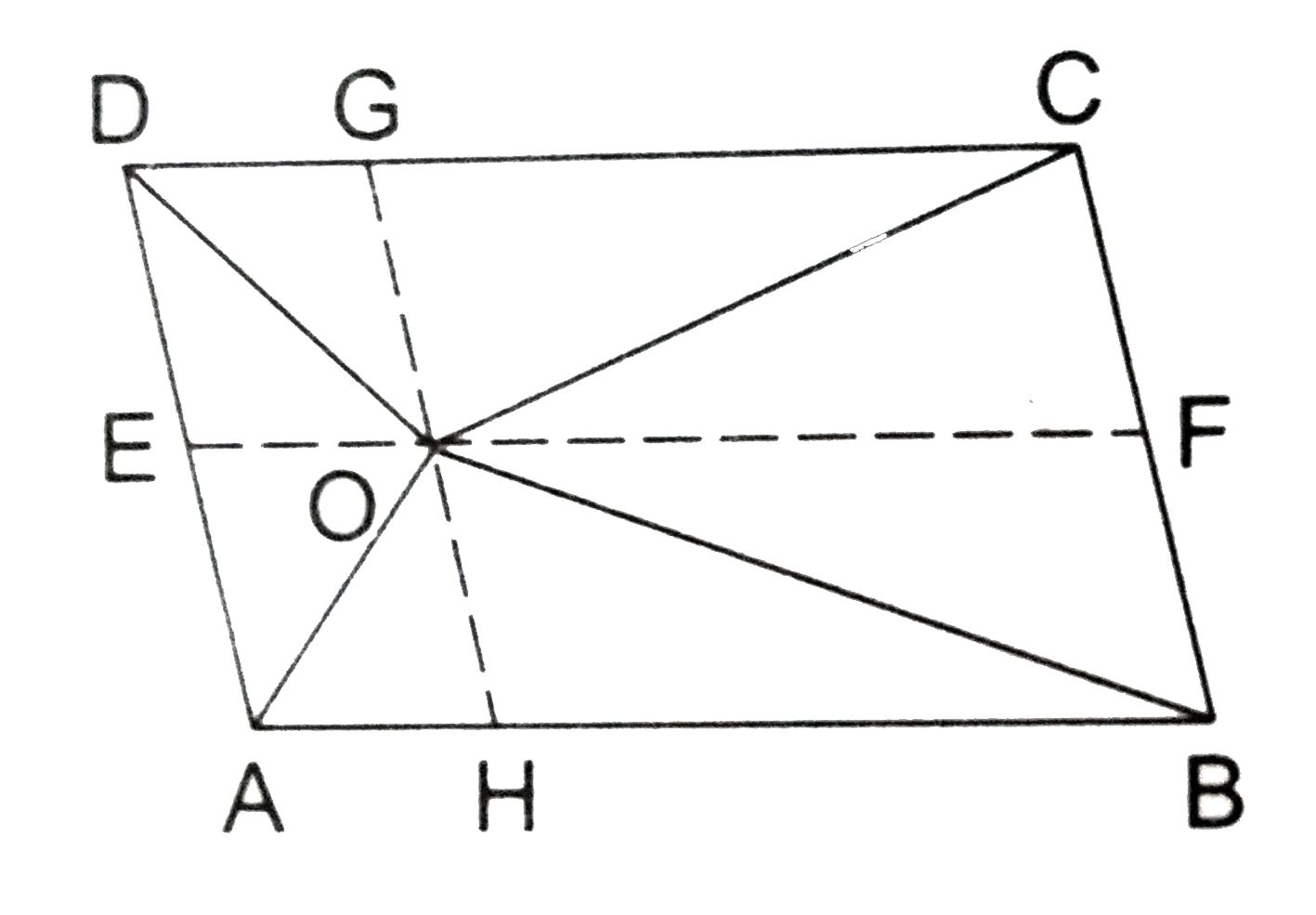
View SolutionABCD एक समांतर चतुर्भुज है तथा O इसके अन्तः क्षेत्र में स्थित कोई बिंदु है सिद्ध कीजिए कि
(i) ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
(ii) ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View Solutionदिए गए चित्र में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है |दर्शाइए की
(i)ar(APB)+ar(PCD)=12ar(ABCD)
ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

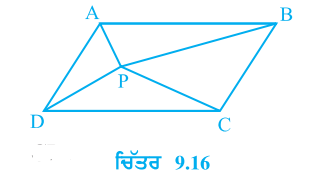
View SolutionIn P is a point in the interior of a parallelogram ABCD. Show that<br>(ii)ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
View SolutionIN the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = 12 ar (ABCD)
(ii) ar (APD) + ar(PBC) = ar(APB) + ar (PCD)
View SolutionIn the given figure, ABED is a parallelogram and DE and EC . Prove that ar (ABF)=ar(BEC)

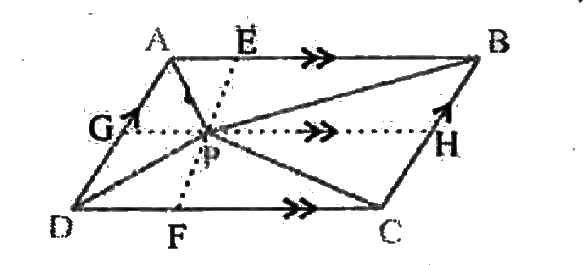
View Solutionਚਿੱਤਰ 9.16 ਵਿਚ, ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੇ ਅੰਦਰ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ P ਹੈ। ਦਰਸਾਉ ਕਿ (i) ar(APB)+ar(PCD)=12ar(ABCD) (ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD) [ਸੰਕੇਤ:-P ਵਿੱਚੋਂ ਲੰਘਦੀ AB ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ।]
View Solution

