चित्र में, ABC एक समकोण त्रिभुज A पर समकोण है। इसकी भुजाओं BC , CA तथा AB पर क्रमशः BCED , ACFG तथा ABMN वर्ग है। रेखाखण्ड , भुजा BC को Y पर मिलती है। सिद्ध कीजिए कि
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
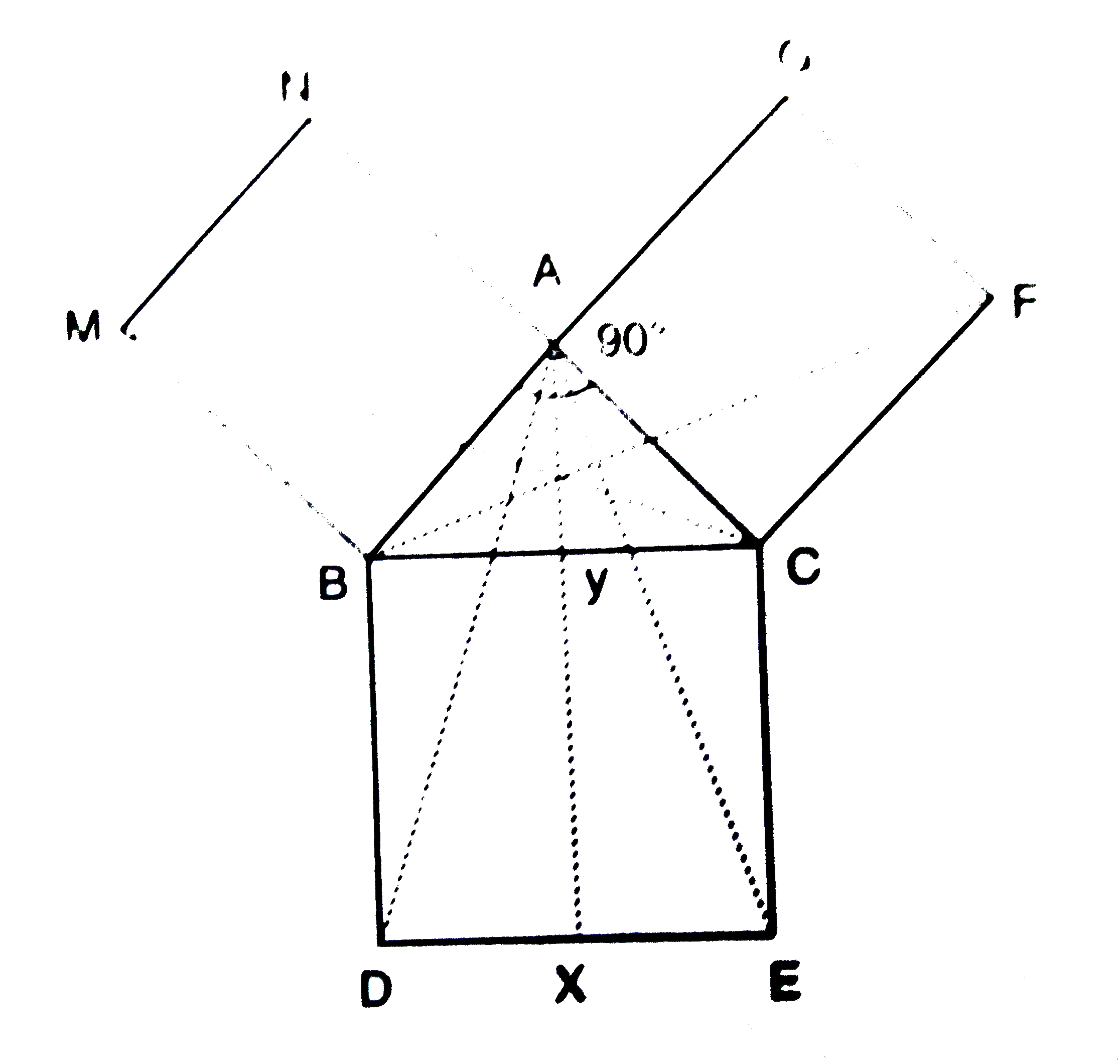
(i) और में,
तथा
अतः भुजा-कोण-भुजा सर्वांगसमता अभिगृहित से,
...(i)
(ii ) स्पष्ट है कि ABD और आयत BYXD एक ही आधार BD और एक हे समांतर रेखाओं AX और BD के बीच स्थित है।
(आयत BYXD)
ar( आयत BYXD)
ar( आयत BYXD)
(iii) चूँकि त्रिभुज MBC और वर्ग MBAN एक ही आधार MB और एक ही समांतर रेखाओं AB एवं NC के बीच स्थित है।
...(iii)
(ii ) और (iii ) से,
ar(वर्ग MBAN) = ar( आयत BYXD)
(iv ) त्रिभुज FCB और ACE में,
तथा
अतः भुजा-कोण-भुजा सर्वांगसमता अभिगृहित से,
(v ) स्पष्ट है कि
स्पष्ट है कि और आयत CYXE एक ही आधार CE और एक ही समांतर रेखाओं CE और AX के बीच स्थित है।
...(iv)
(vi ) स्पष्ट है, कि एवं आयत FCAG एक ही आधार FC और एक ही समांतर रेखाओं FC और BG के बीच स्थित है।
(iv ) और (v ) से,
(vii ) में, पाइथागोरस प्रमेय के प्रयोग से
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:अति लघुत्तरात्मक प्रश्न
Explore 9 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:बहु विकल्पीय प्रश्न
Explore 20 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 15.2
Explore 4 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण Book:RD SHARMAChapter:संख्यिकीय आंकड़ों का आलेखीय निरूपण Exercise:बहु विकल्पीय प्रश्न
Explore 8 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:बहु विकल्पीय प्रश्न
Explore 17 Videos
Similar Questions
यदि ABC व BDE दो समबाहु त्रिभुज इस प्रकार है कि बिंदु D भुजा BC का मध्य बिंदु है, तो त्रिभुज ABC और त्रिभुज BDE के क्षेत्रफल का अनुपात ज्ञात करो।
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है। AE⊥DC तथा CF⊥AD । यदि AB = 16 सेमी, AE = 8 सेमी तथा CF = 10 सेमी , तो AD का मान ज्ञात कीजिये ।
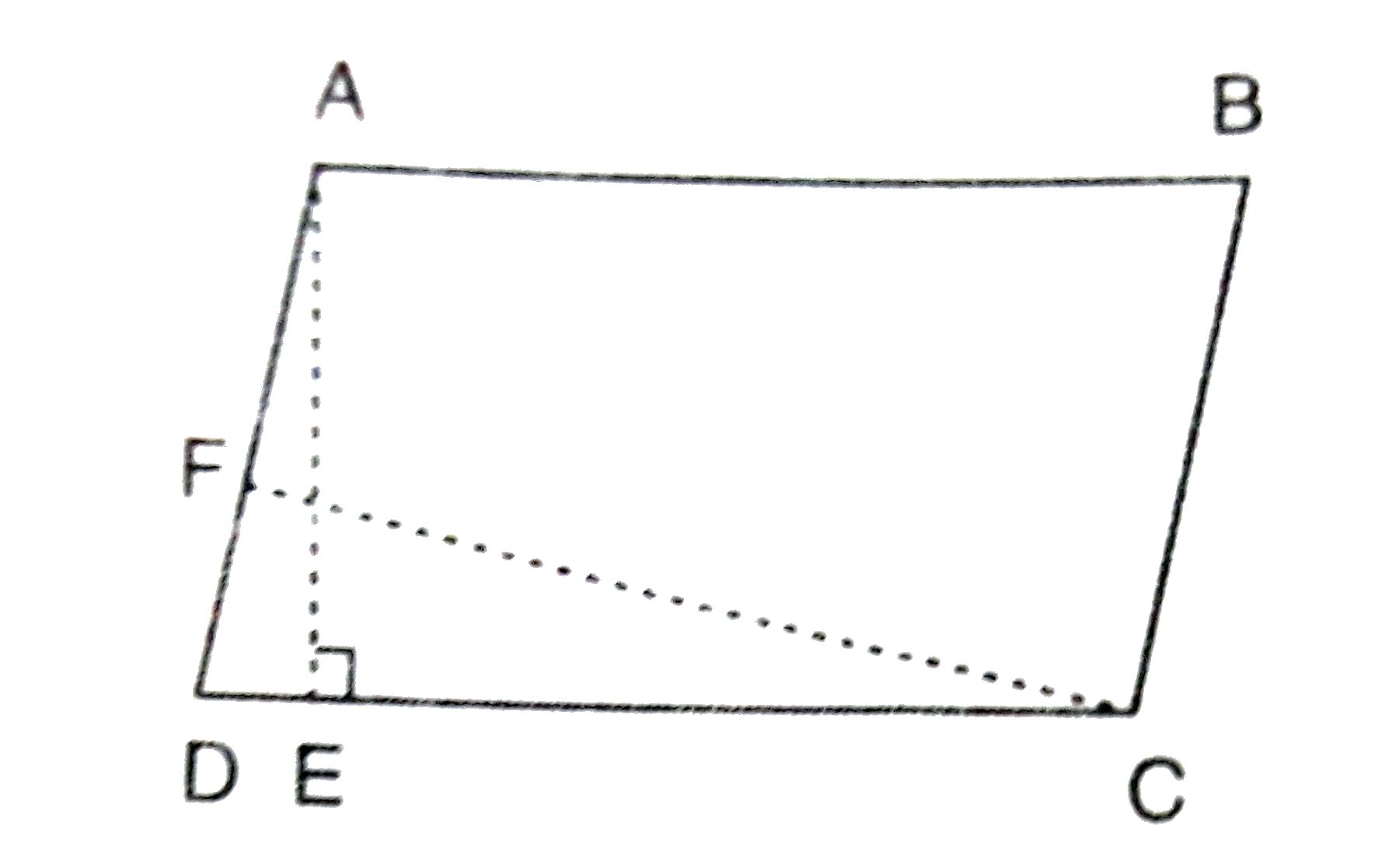
View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
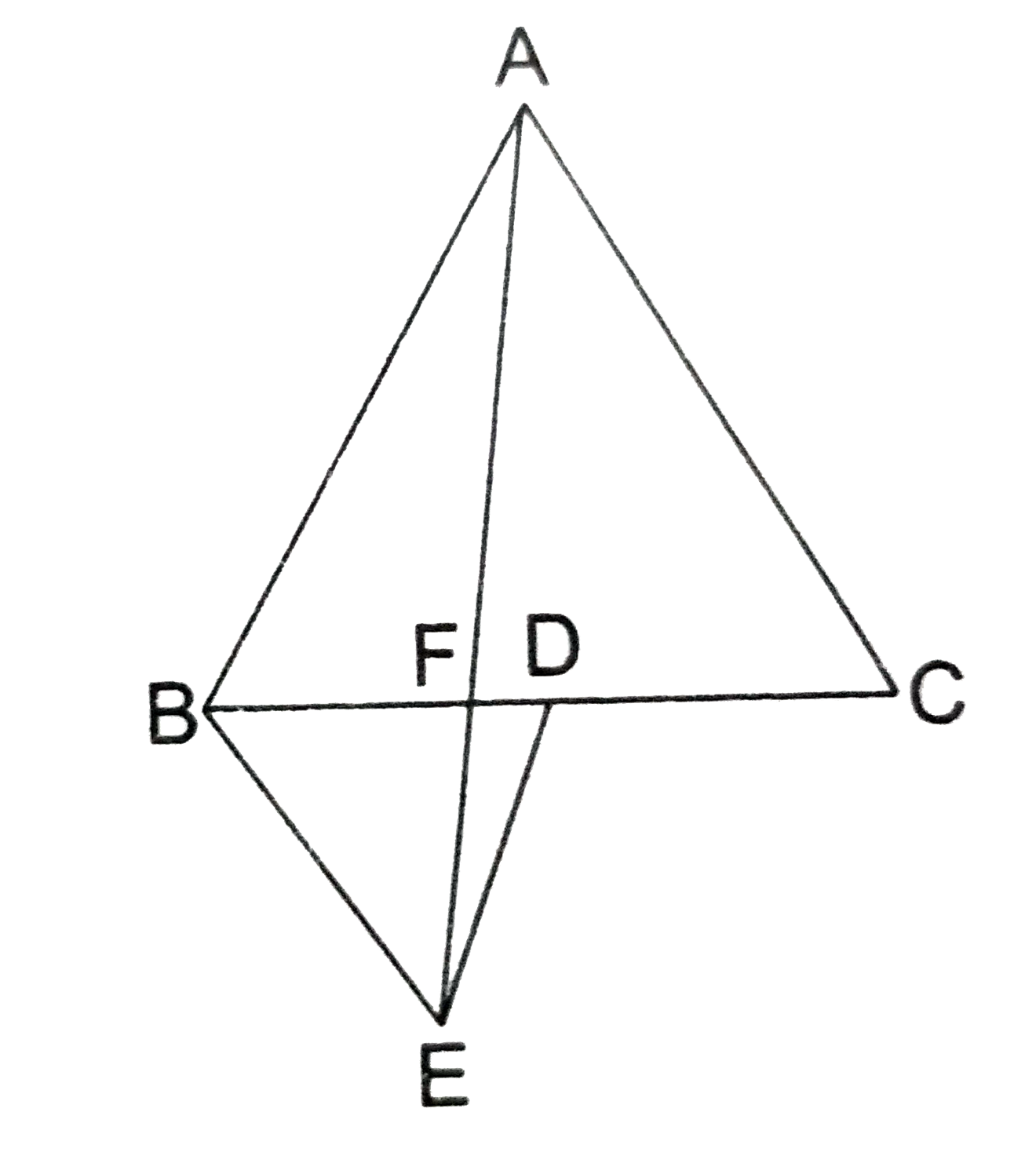
View Solutionदी गए आकृति में ABC एक समकोण त्रिभुज है जिसके कोण A समकोण है | BCED,ACFG और ABMN क्रमशः भुजाओं BC ,CA और AB पर बने वर्ग है| रेखाखण्ड AX⊥DE भुजा BC से बिंदु Y पर मिलता हैं |दर्शाइए की :
(i)ΔMBC≡ΔABD
(ii)ar(BYXD)=2ar(MBC)
(iii)ar(BYXD)=ar(ABMN)
(iv) ΔFCB=ΔACE
(v)ar(CYXE)=2ar(FCB)
(vi)ar(CYXE)=ar(ACFG)
(vii)ar(BCED)=ar(ABMN)+ar(ACFG)
(viii)BC2=AB2+AC2
(##KCSHINMATIXC11SLV032_Q01##)
View SolutionF,Cl, Br ,I and Ar are collectively known as ____________.
View SolutionFactorise:
ar+br+at+bt
View SolutionIn the following figure , ABC is a right triangle right angled at A. BCED ACFG and ABMN and squares on the sides BC, CA and AB respectively , Line segement AX ⊥ DE meets BC at Y. Show that
(i) ti⟩MBC=ti⟩(MBC)
(ii) ar (BXYD) = 2 ar (MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ti⟩FCB=ti⟩ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE ) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
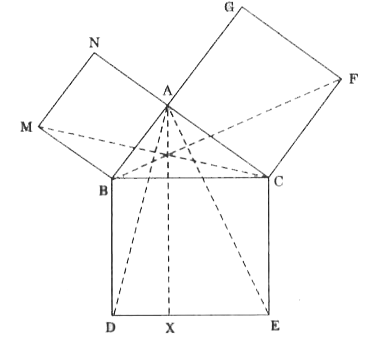
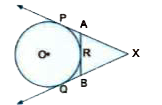
View SolutionIn the Fig Prove that XA+AR=XB+BR.
View Solutionगुणनखण्ड निकालें:
ar+br+at+bt
View Solutionar + br + at + bt = __
View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BYXD) =2 ar (MBC)
View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BYXD) = ar (ABMN)
View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BCED) =ar (ABMN) + ar (ACFG)
View Solution

