यदि त्रिभुज ABC की AD एक माध्यिका है, तो सिद्ध करो कि त्रिभुज ADB और त्रिभुज ADC का क्षेत्रफल बराबर है । यदि माध्यिका AD का मध्य बिंदु G हो, तो सिद्ध करो कि
ar(ΔBGC)=2ar(ΔAGC) है।
AM⊥BC खींचिए।
चूँकि AD,ΔABC की माध्यिका है।
∴BD=DC
⇒BD×AM=DC×AM
⇒12(BD×AM)=12(DC×AM)
⇒ar(ΔABD)=ar(ΔACD) ... (i)
पुनः ΔBGC में, GD एक माध्यिका है।
∴ar(BGD)=ar(CGD) ...(ii)
तथा ΔACD में CG एक माध्यिका है।
∴ar(AGC)=ar(ΔCGD) ... (ii)
(ii) तथा (iii ) से
ar(ΔBGD)=ar(ΔAGC) ...(ii)
किन्तु ar(ΔBGC)=2ar(BGD)
∴ar(BGC)=2ar(ΔAGC)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:अति लघुत्तरात्मक प्रश्न
Explore 9 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:बहु विकल्पीय प्रश्न
Explore 20 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 15.2
Explore 4 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण Book:RD SHARMAChapter:संख्यिकीय आंकड़ों का आलेखीय निरूपण Exercise:बहु विकल्पीय प्रश्न
Explore 8 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:बहु विकल्पीय प्रश्न
Explore 17 Videos
Similar Questions
यदि ABC व BDE दो समबाहु त्रिभुज इस प्रकार है कि बिंदु D भुजा BC का मध्य बिंदु है, तो त्रिभुज ABC और त्रिभुज BDE के क्षेत्रफल का अनुपात ज्ञात करो।
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है। AE⊥DC तथा CF⊥AD । यदि AB = 16 सेमी, AE = 8 सेमी तथा CF = 10 सेमी , तो AD का मान ज्ञात कीजिये ।
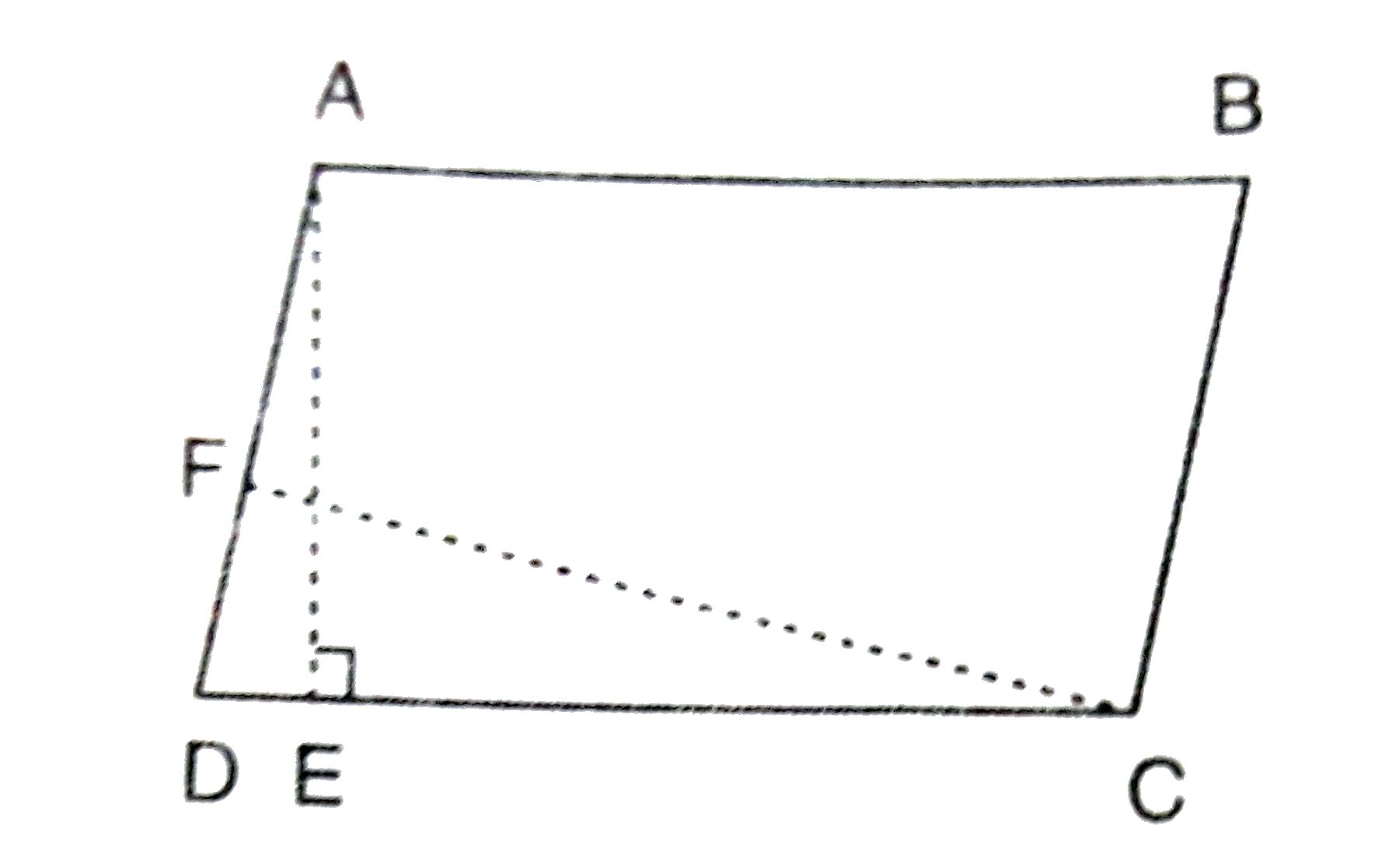
View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View Solutionत्रिभुज ABC में कोण C समकोण है । यदि बिंदु A और B निर्देशांक क्रमशः (−3,4) और (3,−4)हो , तो सिद्ध कीजिये की ΔABC के परिवृत्त का समीकरण x2+y2=25 होगा ।
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionयदि A सममित आव्यूह हो, तो सिद्ध करो कि M'AM भी सममित आव्यूह होगा|
View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात किजिए जिसके शीर्ष बिंदु A(1,1,1),B(1,2,3) और C(2,3,4) है।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि A, B, C, D समष्टि (space) में चार बिन्दु हैं, तो सिद्ध कीजिए कि |AB×CD+BC×AD+CA×BD|=4 ( त्रिभुज ABC का क्षेत्रफल )
View Solutionएक ΔABC में, AB = ri + j, AC =si-j, यदि त्रिभुज का क्षेत्रफल इकाई परिमाण का है। तब,
View SolutionIn triangle ABC AD, BE, CF are medians. If the area of the triangle DGC is 20cm^2 , then the area of triangle AGF + the area of triangle BGF is equal to: त्रिभुज ABC में, AD, BE और CF मध्यरेखा हैं और G त्रिभुज का केन्द्रक है। यदि त्रिभुज DGC का क्षेत्रफल 20cm^2 है, तो त्रिभुज AGF का क्षेत्रफल+ त्रिभुज BGF का क्षेत्रफल किसके बराबर है:
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. If the area of triangle ABC is 136 cm^2 , then the area of triangle BDE is equal to: ABC और BDE दो समबाहु त्रिभुज हैं जेसे D, BC का मध्य-बिंदु है। यदि त्रिभुज ABC का क्षेत्रफल 136 cm^2 , है, तो त्रिभुज BDE का क्षेत्रफल ज्ञात करे
View Solution

