ABCD एक समांतर चतुर्भुज है तथा O इसके अन्तः क्षेत्र में स्थित कोई बिंदु है सिद्ध कीजिए कि
(i) ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
(ii) ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)
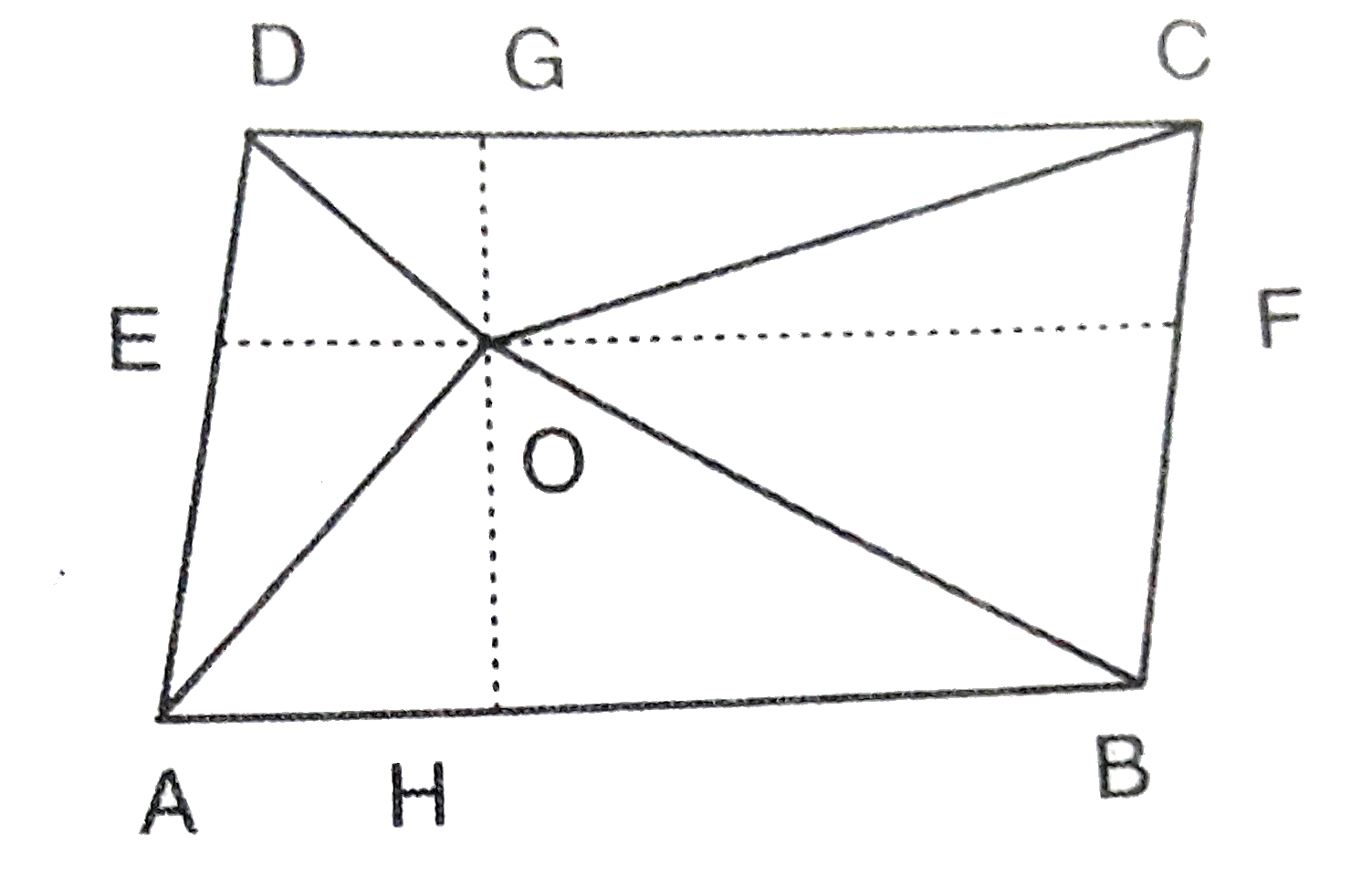
दिया है : एक समांतर चतुर्भुज ABCD तह इसके अन्तः क्षेत्र में स्थित कोई बिंदु O है ।
सिद्ध करना है : ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
रचना : EOF ।। AB तथा GOH ।। AD खींचिए ।
उपपत्ति : चूँकि
GH ।। AD तथा EF ।। DC
∴ OG ।। DE तथा OE ।। GD
⇒ EOGD एक समांतर चतुर्भुज है।
इसी प्रकार, EAHO , HBFO तथा FOGC समांतर चतुर्भुज है।
चूँकि समांतर चतुर्भुज EOGD का एक विकर्ण OD है।
⇒ar(ΔEOD)=ar(ΔDOG) ...(i)
समांतर चतुर्भुज EAHO का विकर्ण OA है।
⇒ar(ΔEOA)=ar(ΔAOH) ... (ii)
समांतर चतुर्भुज HBFO का विकर्ण OB है।
⇒ar(ΔBOF)=ar(ΔBOH) .... (iii)
समांतर चतुर्भुज FOGC का विकर्ण OC है।
ar(ΔFOC)=ar(ΔCOG) ...(iv)
(i), (ii), (iii) तथा (iv ) के सांगत पक्षों को जोड़ने पर,
ar(ΔEOD)+ar(ΔEOA)+ar(ΔBOF)+ar(ΔFOC)
=ar(ΔDOG+ar(ΔAOH)+ar(ΔBOH)+ar(ΔCOG)
⇒ar(ΔAOD)+ar(ΔBOC)=ar(ΔAOB)+ar(ΔCOD)
(ii ) चूँकि ΔAOB तथा समांतर चतुर्भुज ABFE एक ही आधार AB तथा दो समांतर रेखाओं AB तथा EF के बीच स्थित है।
∴ar(ΔAOB)=12ar(।।gmABFE) ... (v)
इसी प्रकार,
ar(ΔCOD)=12ar(।।gmDEFC) ...(vi)
(v ) तथा (vi ) के संगत पक्षों को जोड़ने पर
ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:व्याख्यात्मक उदाहरण
Explore 1 Video
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 15.1
Explore 6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण Book:RD SHARMAChapter:संख्यिकीय आंकड़ों का आलेखीय निरूपण Exercise:बहु विकल्पीय प्रश्न
Explore 8 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:बहु विकल्पीय प्रश्न
Explore 17 Videos
Similar Questions
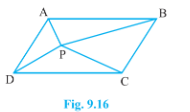
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View Solutionआकृति में में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(APB)+ar(PCD)=12ar(ABCD)
(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View Solutionसमलम्ब ABCD में यदि AB=13CD और ar(ΔAOB)=21cm2 तो ar(ΔCOD) ज्ञात कीजिए।
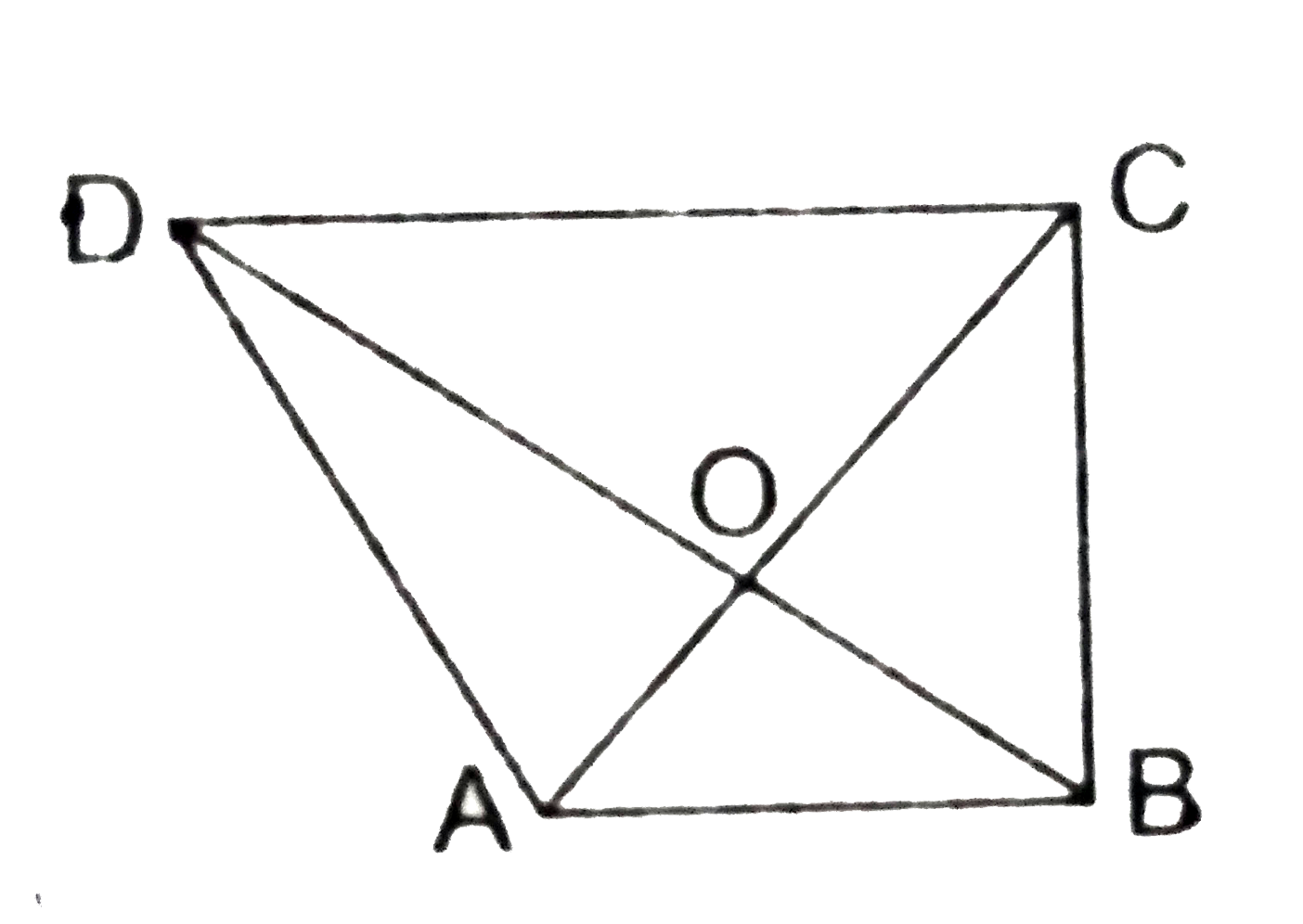
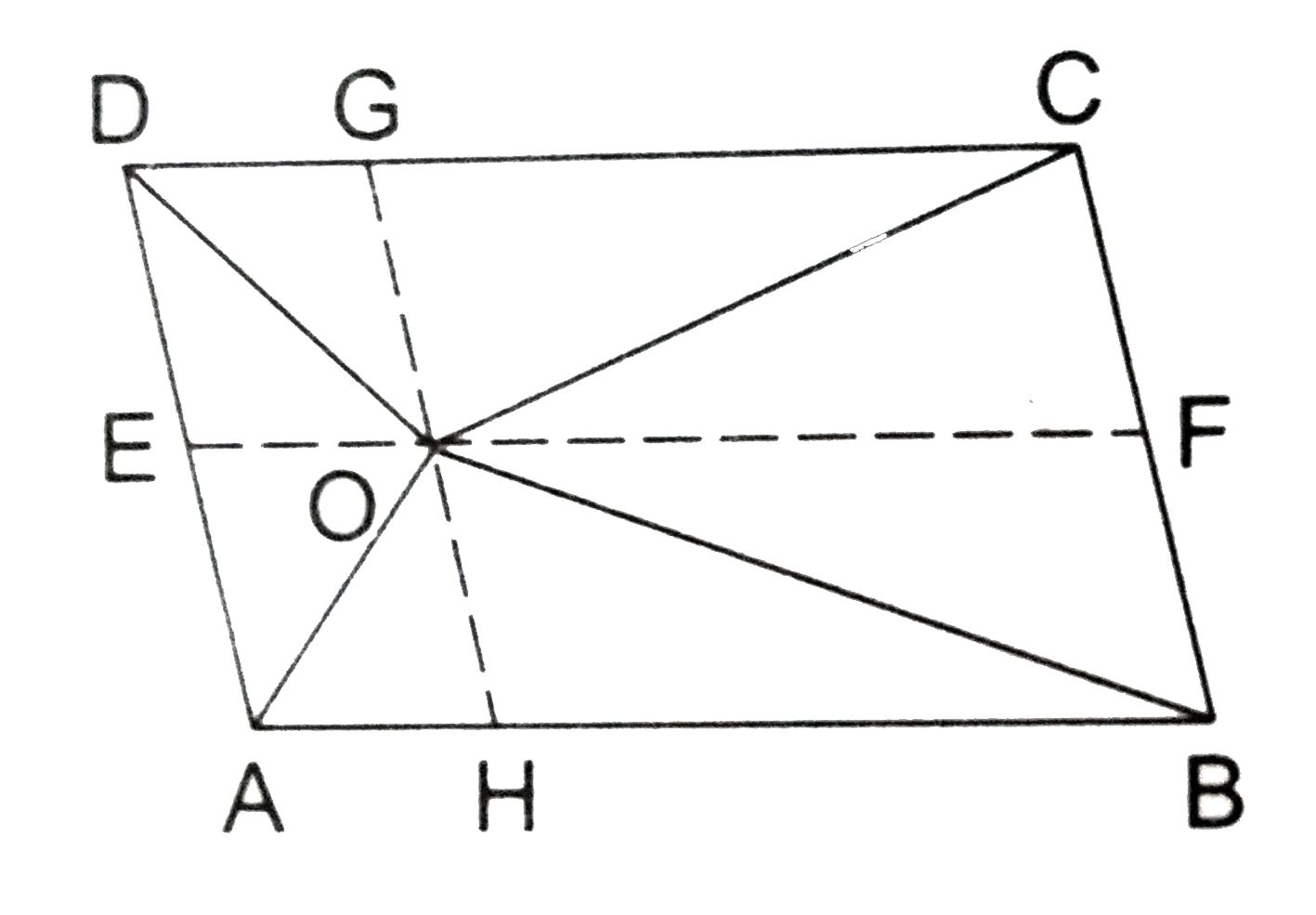
View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
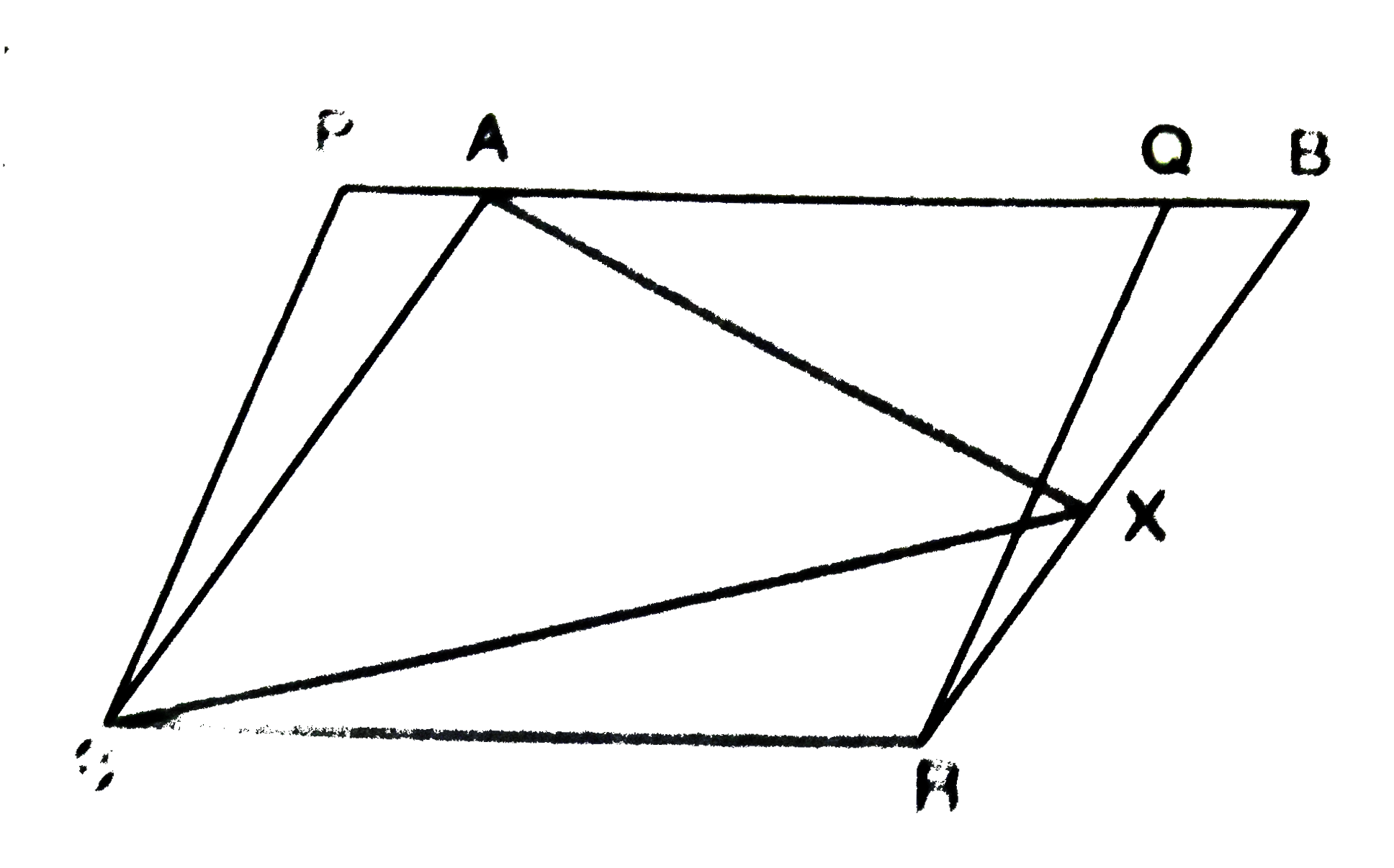
View Solutionचित्र में PQRS तथा ABRS समान्तर चतुर्भुज है तथा X भुजा BR पर स्थित कोई बिंदु है। दर्शाए कि
(i)ar(||gmPQRS)=ar(||gmABRS) (ii)ar(ΔAXS)=12ar(||gmPQRS)
View Solutionएक चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर इस प्रकार प्रतिच्छेद करते हैं कि ar(ΔAOD)=ar(ΔBOC) है । सिद्ध करों कि ABCD एक समलम्ब है।
View Solutionचित्र में, चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर प्रतिच्छेद इस प्रकार करते है कि OB = OD है। यदि AB = CD हो तो दर्शाइए कि
(i) ar(ΔAOD)=ar(ΔBOC)
(ii) ar(ΔABD)=ar(ΔABC)
(iii) DA ।। CB अथवा, ABCD एक समांतर चतुर्भुज है।
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
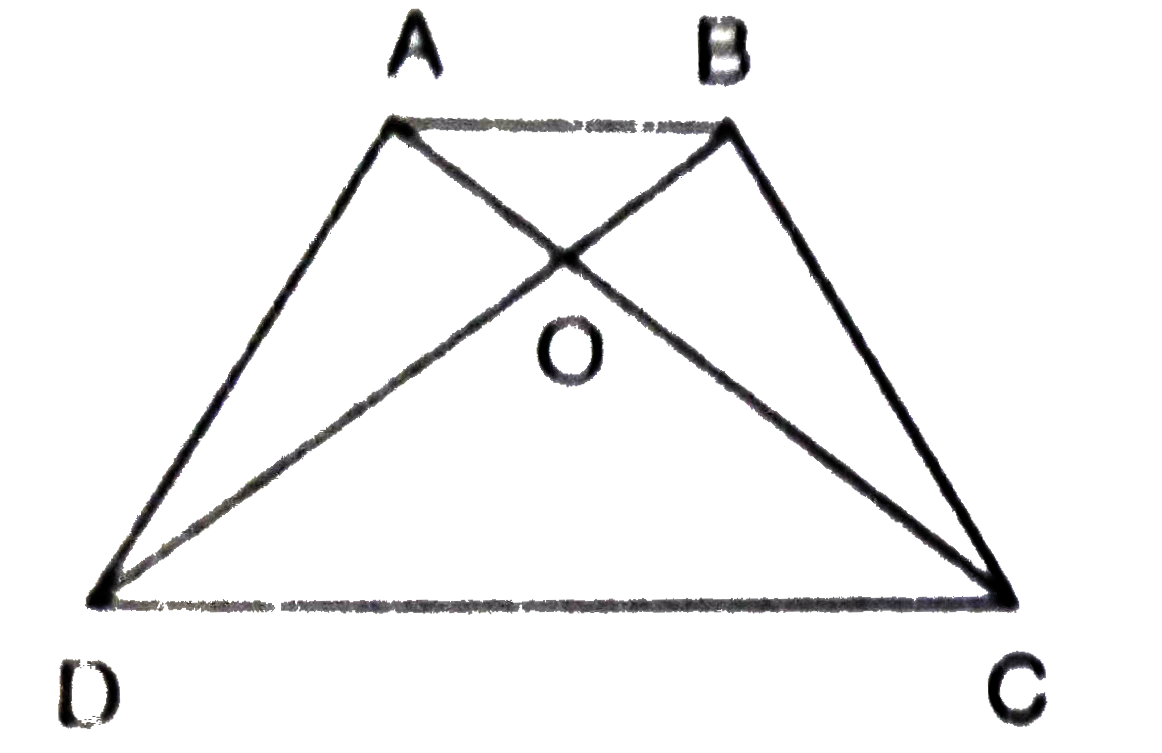
View Solutionचित्र में, यदि ABCD एक समलम्ब है जिसमें AB ।। DC तो सिद्ध कीजिए कि
ar(ΔAOD)=ar(ΔBOC)
View SolutionABCD एक समांतर चतुर्भुज है जिसके विकर्ण O पर प्रतिच्छेद करते है। यदि BO पर कोई बिंदु P हो तो सिद्ध कीजिए कि :
(i)ar(ΔADO)=ar(ΔCDO) (ii)ar(ΔABP)=ar(ΔCBP)
View Solution

