चित्र में, चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर इस प्रकार प्रतिच्छेद करते हैं। कि OB = OD है। यदि AB = CD हो, तो दर्शाइए कि
(i) ar(ΔAOB)=ar(ΔDOC)
(ii) ar(ΔACB)=ar(ΔDCB)
(iii) DA ।। CB अथवा, ABCD एक समांतर चतुर्भुज है।
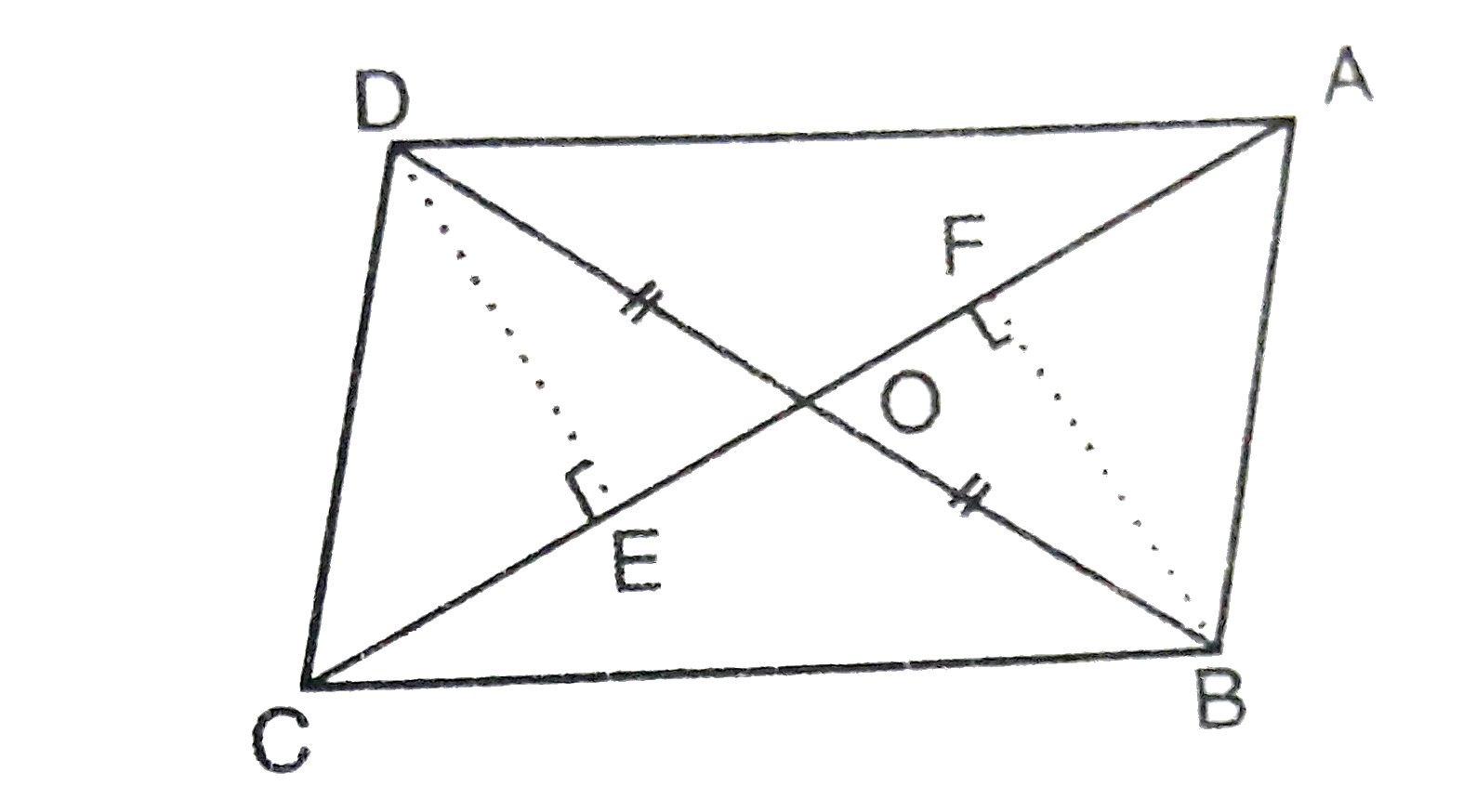
(i ) त्रिभुज DOE तथा BOF में,
OB=OD [दिया है]
∠DOE=∠BOF [शीर्षाभिमुख कोण]
∠DEO=∠BFO
अतः कोण-कोण-भुजा सर्वांगसमता अभिग्रहित से,
ΔDOE=ΔBOF
⇒ar(ΔDOE)=ar(ΔBOF)andDE=BF ... (i)
त्रिभुज DEC तथा BFA में,
∠DEC=∠BFA=90∘
DE=BF
तथा CD=AB
अतः RHS सर्वांगसम अभिग्रहित से,
ΔCDE≅ΔABF
⇒ar(ΔCDE)=ar(ΔABF)and∠DCE=∠BAF ... (ii)
(i ) तथा (ii ) से,
ar(ΔDOE)+ar(ΔCDE)=ar(ΔBOF)+ar(ΔABF)
⇒(ΔCOD)=ar(ΔAOB)
(ii) दिया है,
ar(ΔAOB)=ar(ΔCOD)
⇒(ΔAOB)+ar(ΔBOC)=ar(ΔCOD)+ar(ΔBOC)
⇒ar(ΔACB)=ar(ΔDCB)
(iii) स्पष्ट है कि
∠DCE=∠BAF [(ii) से ]
⇒∠ACD=∠CAB
⇒ DC ।। AB
तथा DC=AB [दिया है]
अतः ABCD एक समांतर चतुर्भुज है।
अतः DA ।। CB
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण
1 Video
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.1
6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionMatch the following Column A to Column B

View Solutionआकृति में चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB=OD है । यदि AB=CD है , तो दर्शाइए कि
(i) ar(DOC)=ar(AOB)
(ii) ar(DCB)=ar(ACB)
(iii) DA∣∣CB या ABCD एक समांतर चतुर्भुज है ।
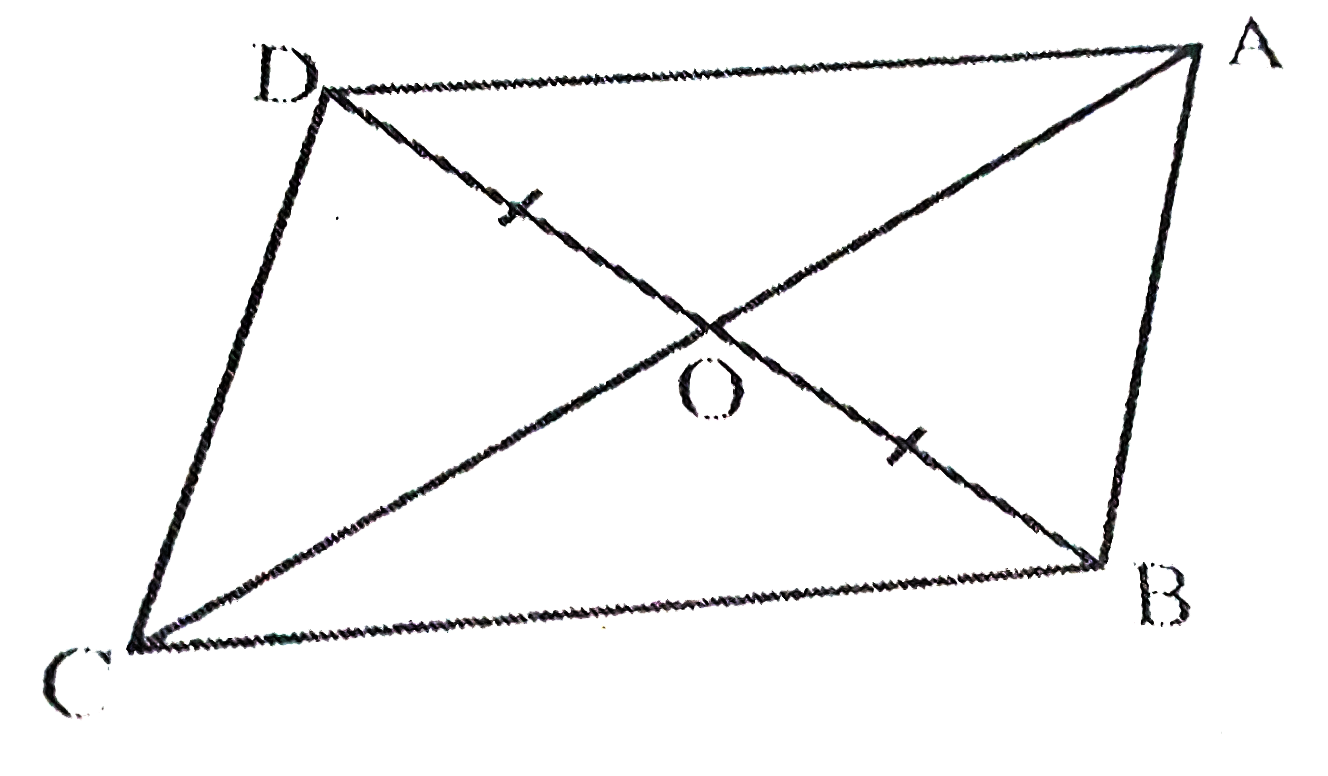
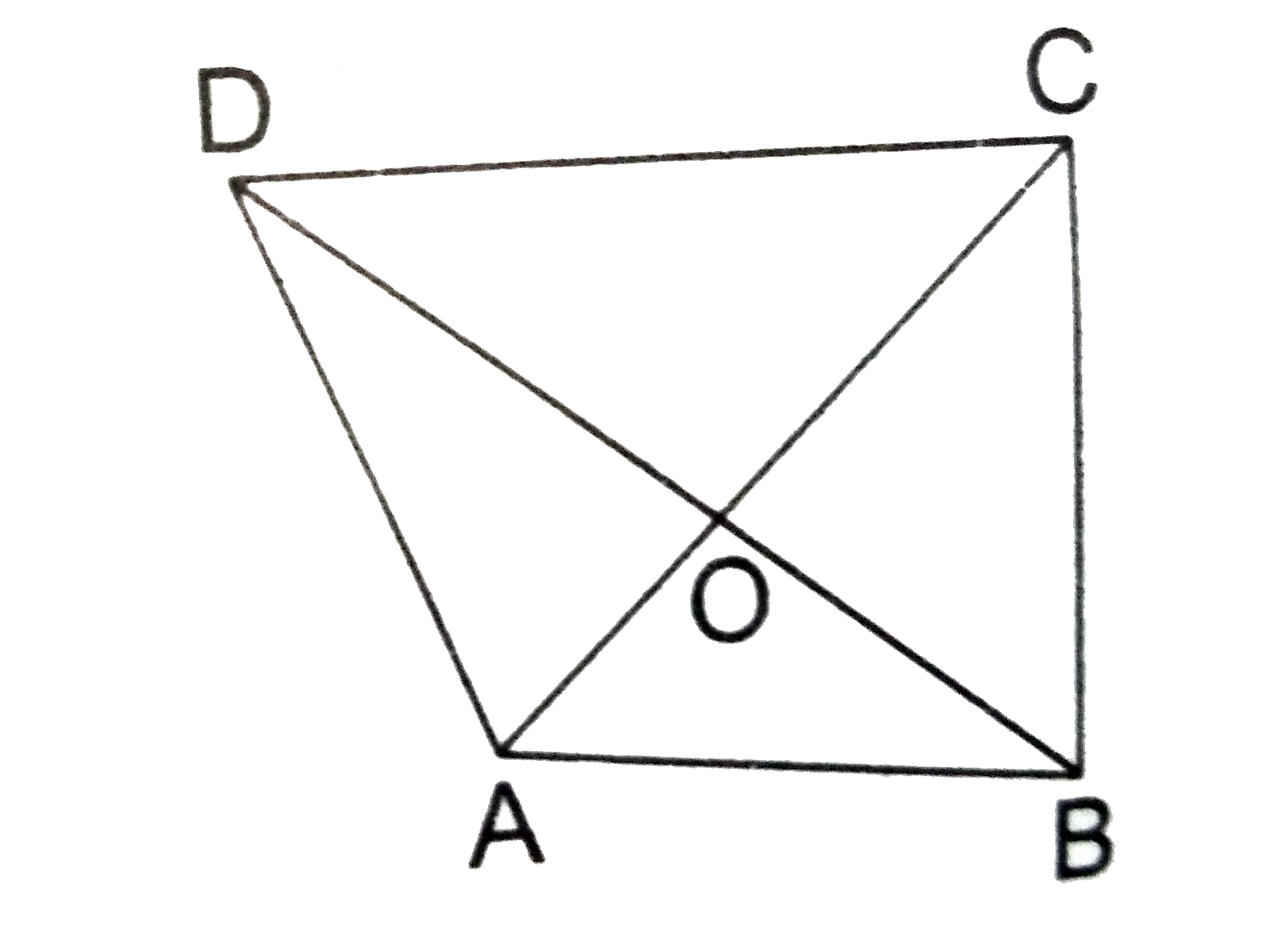
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
View Solutionचित्र में, चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर प्रतिच्छेद इस प्रकार करते है कि OB = OD है। यदि AB = CD हो तो दर्शाइए कि
(i) ar(ΔAOD)=ar(ΔBOC)
(ii) ar(ΔABD)=ar(ΔABC)
(iii) DA ।। CB अथवा, ABCD एक समांतर चतुर्भुज है।
View SolutionABCD एक समांतर चतुर्भुज है तथा O इसके अन्तः क्षेत्र में स्थित कोई बिंदु है सिद्ध कीजिए कि
(i) ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
(ii) ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)
View Solutionदिए गए चित्र में चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते है की OB = OD है|यदि AB =CD है ,तो दर्शाइए की
(i)ar(DOC)=ar(AOB)
(ii)ar(DCB)=ar(ACB)
(iii)DA∣∣CB या ABCD एक समांतर चतुर्भुज है|
(##KCSHINMATIXC11SLV028_Q01##)
View SolutionF,Cl, Br ,I and Ar are collectively known as ____________.
View SolutionFactorise:
ar+br+at+bt
View SolutionIn the given figure, diagonals AC and BD of quadrilateral ABCD interset at O such that OB = OD. If AB = CD, then show that :
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram .
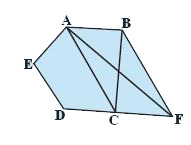
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB)=ar(ΔACF)
(ii) ar(AEDF)=ar(ABCDE)
View Solutionगुणनखण्ड निकालें:
ar+br+at+bt
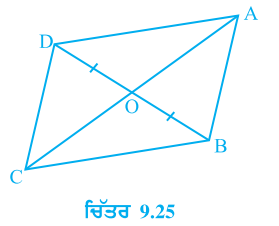
View Solutionਚਿੱਤਰ 9.25 ਵਿੱਚ, ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿਚ ਬਿੰਦੂ O ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦੇ ਹਨ ਕਿ OB=OD ਹੈ। ਜੇਕਰ AB=CD ਹੋਵੇ ਤਾਂ ਦਰਸਾਓ ਕਿ ar (DOC) = ar (AOB) [ਸੰਕੇਤ:- D ਅਤੇ B ਤੋਂ AC ਉੱਤੇ ਲੰਬ ਖਿਚੋ।]
View Solution
