दिए गए चित्र में चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते है की OB = OD है|यदि AB =CD है ,तो दर्शाइए की
(i)ar(DOC)=ar(AOB)
(ii)ar(DCB)=ar(ACB)
(iii)DA∣∣CB या ABCD एक समांतर चतुर्भुज है|
(##KCSHINMATIXC11SLV028_Q01##)
बनावट : D से, DL⊥AC तथा B से BM⊥AC खिंचा|
प्रमाण :(i ) ΔDOL और ΔBOM में
OD=OM [दिया है]
∠DOL=∠BOM [सम्मुख कोण ]
∠DOL=∠BMO [प्रत्येक =90∘ ]
∴ ΔDOL=ΔBOM [ ASA सर्वांगसमता नियम से ]
∴ DL=BM के साथ ही ar(ΔDOL)=ar(ΔBOM) ...(i)
पुनः समकोण ΔDLC और ΔBMA में ltBrgt ∠DLC=∠BMC=90∘
कर्ण CD =कर्ण AB [दिया है ]
तथा DL=BM [ऊपर सिद्ध किया जा चूका है]
∴ ΔDLC≡ΔBMA [RHS सर्वांसमता नियम से]
अतः ar(ΔDLC)=ar(ΔBMA) ...(ii)
ar(ΔDOL)+ar(ΔDLC)=ar(ΔBOM)+ar(ΔBMA)
अर्थात ar(ΔDOC)=ar(ΔAOB) ...(iii)
(ii) समीकरण (iii ) के दोनों तरफ ar(ΔAOB) जोड़ देने पर
ar(ΔDOC)+ar(ΔCOB)=ar(ΔAOB)+ar(ΔCOB)
⇒ ar(ΔDCB)=ar(ΔACB)
(iii) चूँकि ΔDCB और ΔACB एक ही आधार CB पर खड़े है तथा (iv ) से उनके क्षेत्रफल बराबर है, इसलिए वे एक ही समांतर रेखाओं के बीच स्थित होंगें|
∴ DA∣∣CB
फिर ∵ ΔDOL≡ΔBOM∴OL=OM
तथा ΔDLC≡ΔBMA∴LC=MA
जोड़ने पर OL+LC=OM+MA अर्थात OC=OA इस प्रकार चतुर्भुज के कर्ण एक-दूसरे को O बिंदु पर समद्विभाजित करते है अतः ABCD एक समांतर चतुर्भुज है|
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 11.1
24 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न
7 Videos
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - वस्तुनिष्ठ प्रश्न
9 Videos
- हीरोन का सूत्र BOOK - KC SINHACHAPTER - हीरोन का सूत्र EXERCISE - वस्तुनिष्ठ प्रश्न
13 Videos
Similar Questions
रिक्त स्थान को भरें :
(i) सर्वांगसम आयतों के क्षेत्रफल ...........होते है|
(ii) किसी समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का .....होता है
(iii) समलम्ब का क्षेत्रफल उसके समांतर भुजाओं के बीच की दुरी तथा समांतर भुजाओं के योग के गुणनफल का ......होता है|
(iv) सर्वांगसम त्रिभुजों के क्षेत्रफल ........होते है|
(v) एक ही आधार तथा एक ही समांतर रेखाओं के मध्य बने त्रिभुज क्षेत्रफल में ...........होते है|
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
View Solutionयदि किसी ΔABC में BC=a,CA=b AB=c हो तो ΔABC की अर्धपरिमिति है
View Solutionआकृति में चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB=OD है । यदि AB=CD है , तो दर्शाइए कि
(i) ar(DOC)=ar(AOB)
(ii) ar(DCB)=ar(ACB)
(iii) DA∣∣CB या ABCD एक समांतर चतुर्भुज है ।
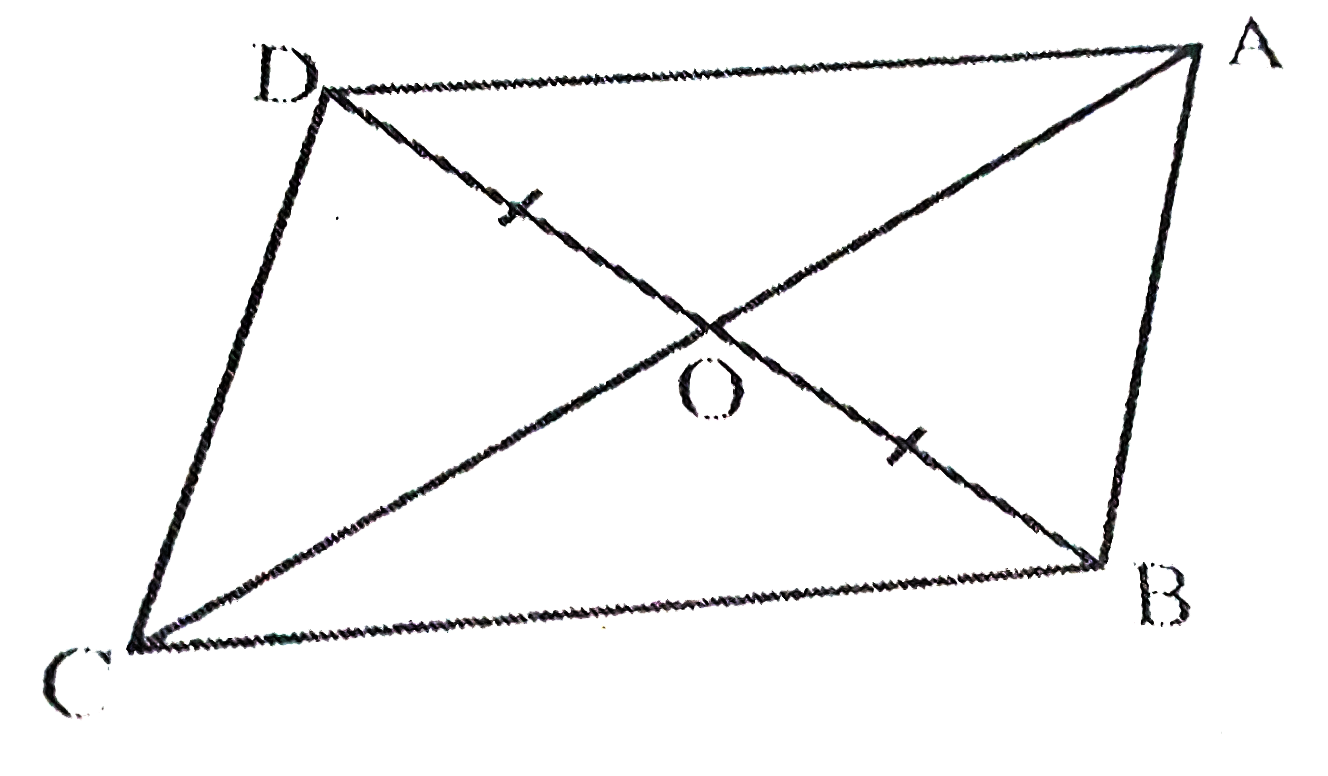
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
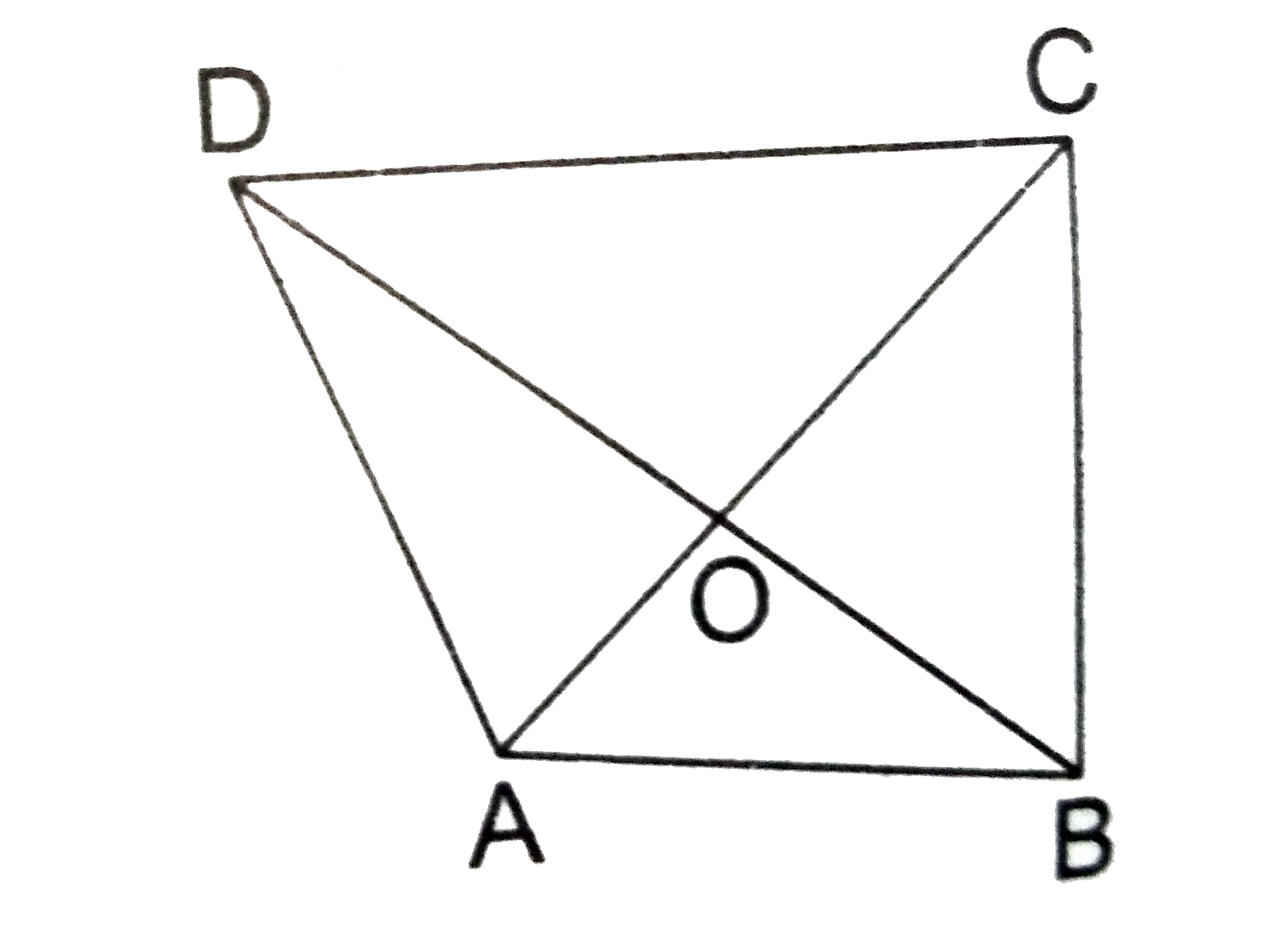
View Solutionचित्र में, चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर प्रतिच्छेद इस प्रकार करते है कि OB = OD है। यदि AB = CD हो तो दर्शाइए कि
(i) ar(ΔAOD)=ar(ΔBOC)
(ii) ar(ΔABD)=ar(ΔABC)
(iii) DA ।। CB अथवा, ABCD एक समांतर चतुर्भुज है।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View SolutionFactorise:
ar+br+at+bt
View SolutionIn the given figure, diagonals AC and BD of quadrilateral ABCD interset at O such that OB = OD. If AB = CD, then show that :
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram .
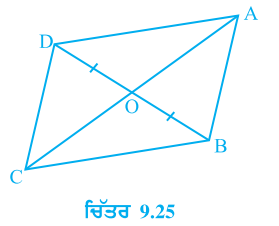
View Solutionਚਿੱਤਰ 9.25 ਵਿੱਚ, ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿਚ ਬਿੰਦੂ O ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦੇ ਹਨ ਕਿ OB=OD ਹੈ। ਜੇਕਰ AB=CD ਹੋਵੇ ਤਾਂ ਦਰਸਾਓ ਕਿ ar (DOC) = ar (AOB) [ਸੰਕੇਤ:- D ਅਤੇ B ਤੋਂ AC ਉੱਤੇ ਲੰਬ ਖਿਚੋ।]
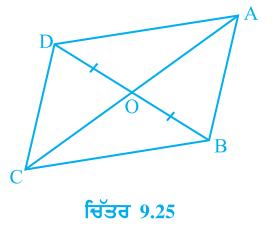
View Solutionਚਿੱਤਰ 9.25 ਵਿੱਚ, ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿਚ ਬਿੰਦੂ O ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦੇ ਹਨ ਕਿ OB=OD ਹੈ। ਜੇਕਰ AB=CD ਹੋਵੇ ਤਾਂ ਦਰਸਾਓ ਕਿ ar (DCB) = ar (ACB) [ਸੰਕੇਤ:- D ਅਤੇ B ਤੋਂ AC ਉੱਤੇ ਲੰਬ ਖਿਚੋ।]
View Solutionar + br + at + bt = __
View SolutionA cyclic Quadrilateral ABCD is such that AB=BC, AD=DC and AC and BD intersect at O. If angle CAD= 46^@ , then the measure of angle AOB is equal to: एक चक्रीय चतुर्भुज ABCD इस प्रकार है की AB = BC, AD = DC और AC और BD पर O पर प्रतिच्छेदित करती है । यदि angle CAD= 46^@ है, तो angle AOB का माप है:
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle ADC = 148^@ . what is the measure of the angle BAC ? ABCD एक चक्रीय चतुर्भुज है, इस प्रकार की AB इसके अंदर वृत्त का व्यास है और angle ADC = 148^@ है। angle BAC का माप कया है
View Solution