In the given figure, the diagonals AC and BD intersects at point O. If OB=OD and AB//DC, prove that :
(i) Area(ΔDOC)=Area(ΔAOB).
(ii) Area(ΔDCB)=Area(ΔACB).
(iii) ABCD is a parallelogram.
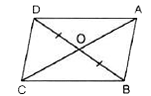
Step by step video & image solution for In the given figure, the diagonals AC and BD intersects at point O. If OB=OD and AB////DC, prove that : (i) "Area" (DeltaDOC)= "Area" (DeltaAOB). (ii) "Area" (DeltaDCB)= "Area" (DeltaACB). (iii) ABCD is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)16videos
AREA THEOREMS
- BOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)12videos
AREA AND PERIMETER OF PLANE FIGURES
- BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA12videos
CHAPTER REVISION (STAGE 2)
Similar Questions
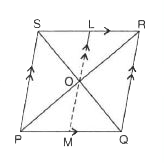
In the given figure, diagonals PR and QS of thr parallelogram PQRS intersect at point O and LM is parallel to PS. Show that :
(i) 2Area(ΔPOS)=Area(//gmPMLS)
(ii) Area(ΔPOS)+Area(ΔQOR)
=12Area(//gmPQRS)
(iii) Area(ΔPOS)+Area(ΔQOR)
=Area(ΔPOQ)+Area(tΔSOR)
 View Solution
View Solution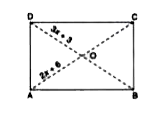
In the given figure, the diagonals AC and BD of a rectangle ABCD intersect each other at point O.
If OA=2x+6 and OD=3x+3, find the value of x.View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO:OD=4:7, find
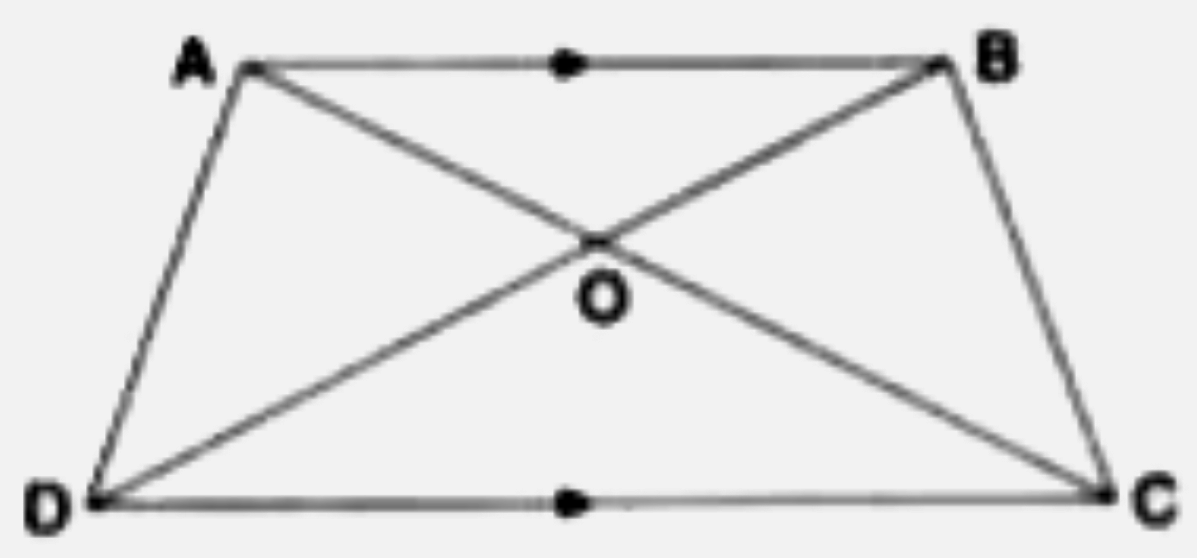
ΔDOC:ΔAOBView SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)
 View Solution
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
ΔAOB is similar to ΔCOD.View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
OA×OD=OB×OC.View SolutionIn the figure, the area of parallelogram ABCD is
 View Solution
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO:OD=4:7, find

ΔAOB:ΔACBView SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO:OD=4:7, find

ΔAOD:ΔAOBView SolutionThe medians of a triangle ABC intersect each other at point G. If one of its medians is AD, Prove that :
(i) Area (ΔABD)=3x Area(ΔBGD)
(ii) Area (ΔACD)=3x Area(ΔCGD)
(iii) Area (ΔBGC)=(1)/(3)x Area(ΔABC)View Solution
