A longitudinal standing wave ℰ = a cos kx- cos ωt is maintained in a homogeneous medium of density ρ. Find the expressions for the space density of a potential energy wp x t; b kinetic energy wk x t. Plot the space density distribution of the total energy ω in the space between the displacement nodes at the moments t = 0 and t = T/4 where T is the oscillation period.
Given ℰ = a cos k x cos ωt a The potential energy density per unit volume is the energy of longitudinal strain. This isb The kinetic energy density is On plotting we get Fig. 37 given in the book p. 332. For example at t = 0and the displacement nodes are at so we do get the figure.
Related Solutions
A longitudinal standing wave is maintained in a homogeneous medium of density . Find the expressions for the space density of
potential energy
kinetic energy
Plot the space density distribution of the total energy in the space between the displacement nodes at the moments and , where is oscillation period.
View SolutionThe equation of a plane standing wave in a homogeneous elastic medium has the form . Plot
(a) and as functions of at the moments and , where is the oscillation period,
the distribution of density of the medium at the moments and in the case of longitudinal oscillation ,
the velocity distribution of particles of the medium at the moment , indicate the directions of velocities at the antinodes, both for longitudinal and transverse oscillation.
View SolutionA longitudinal standing wave is maintained in a homogeneious medium of density . Here is the angular speed and , the wave number and is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the potential energy at a point in this space is
View SolutionA longitudinal standing wave y = a cos kx cos omega t is maintained in a homogeneious medium of density rho . Here omega is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space. The space density of the potential energy PE = E_(p)(x , t) at a point (x , t) in this space is
View SolutionA longitudinal standing wave y = a cos kx cos omega t is maintained in a homogeneious medium of density rho . Here omega is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space. If a graph E ( = E_(p) + E_(k)) versus t , i.e., total space energy density verus time were drawn at the instants of time t = 0 and t = T//4 , between two successive nodes separated by distance lambda//2 which of the following graphs correctly shows the total energy (E) distribution at the two instants.
View SolutionA longitudinal standing wave y = a cos kx cos omega t is maintained in a homogeneious medium of density rho . Here omega is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space. If a graph E ( = E_(p) + E_(k)) versus t , i.e., total space energy density verus time were drawn at the instants of time t = 0 and t = T//4 , between two successive nodes separated by distance lambda//2 which of the following graphs correctly shows the total energy (E) distribution at the two instants.
View SolutionA longitudinal standing wave is maintained in a homogeneious medium of density . Here is the angular speed and , the wave number and is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the kinetic energy . at the point is given by
View SolutionA longitudinal standing wave y = a cos kx cos omega t is maintained in a homogeneious medium of density rho . Here omega is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space. The space density of the kinetic energy . KE = E_(k) ( x, t) at the point (x, t) is given by
View SolutionStanding wave is maintained in a homogeneous rod with cross-sectional area S and density . Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
View SolutionA plane undamped harmonic wave progates in a medium. Find the mean space density of energy becomes equal to at an instant , where is the instant when amplitude is maximum at this location and T is the time period of oscillation.
View SolutionA plane undamped harmonic wave progates in a medium. Find the mean space density of energy becomes equal to W_(0) at an instant t=t(0)+T//6 , where t_(0) is the instant when amplitude is maximum at this location and T is the time period of oscillation.
View SolutionIn a uniform magnetic field of 10^(-5) T in free space, the energy density is u . The electric field which will produce the same energy density in free space is
View SolutionA plane wave xi = a cos ( omega t- kx) propagates in a homongeneous elastic medium, For the moment t=0 draw (a) the plots of xi, delta xi // delta t, and delta xi // deltax vs x, (b) velocity medium direction of the particle of the medium at the points where xi = 0 , for the cases of longitudinal and transverse waves, (c) the approximate plot of density distribution rho (x) of the medium for the case of longitudinal waves.
View Solutionएक दोलक का वायु में आवर्तकाल T है तथा जब यह जल में दोलन करता है तब इसका आवर्तकाल हो जाता है। दोलक के गोलक का घनत्व है (जल का घनत्व = 1)
View Solutioni.The acceleration versus time graph of a partical SHM is shown in the figure . Plot the displacement versus time graph
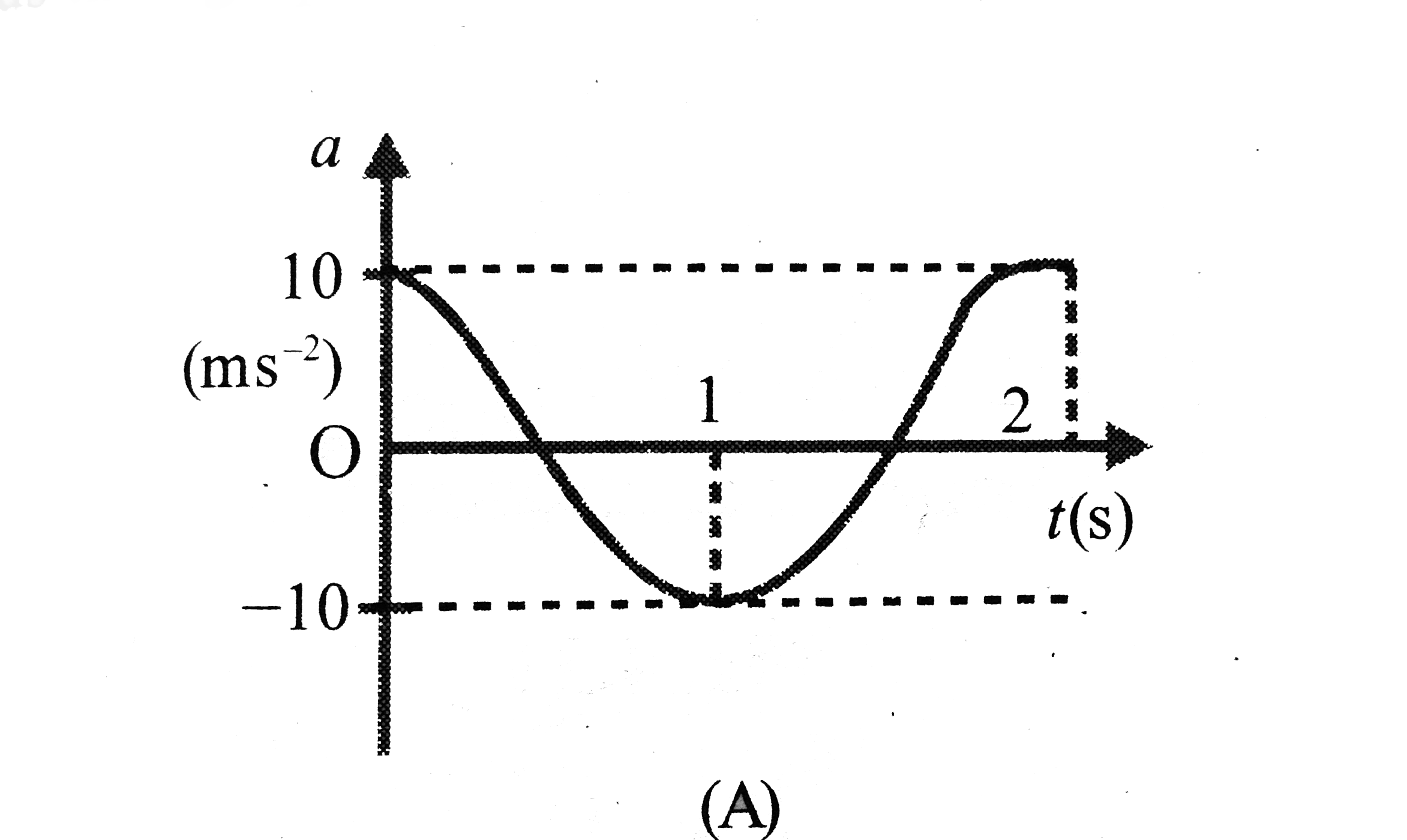
ii. The frequency of oscillation is……..
iii. The displacement amplitude is ………
iv. At , the velocity of the partical is ......
v. The kinetic energy of the partical is maximum at ....... and t = ......
vi. The potential energy is maximum at t = ....... : t = ..... ans t = .........
View Solutioni.The acceleration versus time graph of a partical SHM is shown in the figure . Plot the displacement versus time graph ii. The frection of oscillation is…….. iii. The displacement amplitude is ……… iv. At t = 0 , the velocity of the partical is ...... v. The kinetic energy of the partical is maximum at t = ....... and t = ...... vi. The potential energy is maximum at t = ....... : t = ..... ans t = .........
View SolutionA plane undamped harmonic wave propagates in a medium. Find the mean space density of the total oscillation energy ( :w: ) , if at any point of the medium the space density of the total oscillation energy becomes equal to w_(0) one - sixth of an oscillation perio after passing the displacement maximum
View SolutionStanding wave is maintained in a homogeneous rod with cross-sectional area S and density . Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
View SolutionA standing wave is maintained in a homogeneous rod with cross sectional area and density . Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
View SolutionA standing wave xi= a sin kx. Cos omegat is maintained in a homogeneous rod with cross - sectional area S and density rho . Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
View Solution