A horizontally oriented copper rod of length l= 1.0 m is rotated about a vertical axis passing through its middle. What is the number of rps at which this rod ruptures?
Let us consider an element of rod at a distance x from its rotation axis Fig.. From Newton’s second law in projection form directed towards the rotation axis
Related Solutions
A horizontally oriented copper rod of length / is rotating about a vertical axis passing through its middle. Calculate the rotation frequency at which the rod ruptures. Breaking or rupture strength of copper is sigma and density of copper is rho .
View SolutionA horizontally orientied unifrom copper rod of length is rotating about a vertical axis passing through its centre. Calculate the rotated frequency at which the rod ruptures. Breaking or rupture strength of copper is and density of copper is .
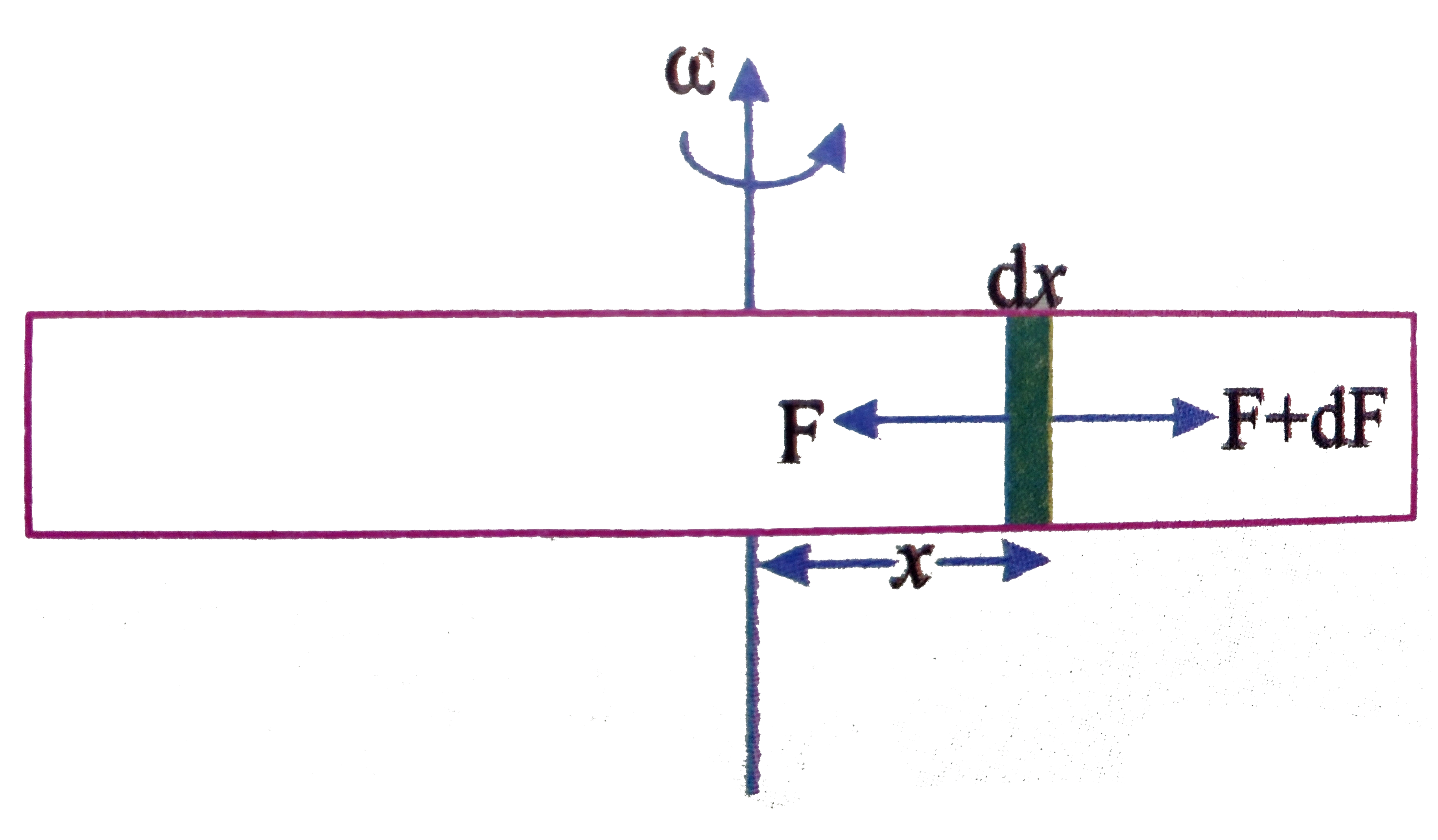
View SolutionA horizontally orientied unifrom copper rod of length l is rotating about a vertical axis passing through its centre. Calculate the rotated frequency at which the rod ruptures. Breaking or rupture strength of copper is sigma and density of copper is rho .
View SolutionWhat will be the breaking strength of the material if a horizontal rod of density and length unity, which is rotating about a vertical axis (passing through its cnetre), ruptures at 10 rps.
View SolutionWhat will be the breaking strength of the material if a horizontal rod of density and length unity, which is rotating about a vertical axis (passing through its centre ), ruptures at 10 rps.
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionMoment of inertia of a thin rod of mass 'M' and length 'L' about the axis perpendicular to the rod and passing through its centre is ............
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass and length rotates in a horizontal plane with an angular velocity about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod is released from rest in the Position shown by slightly displacing it clockwise. Find the hinge reaction at the axis of rotation at the instant the rod turns through. 90^@
View SolutionA rod PQ of mass m and length L is rotated about an axis through P as shown in figure. Find the moment of inertia of the rod about the axis of rotation.

View SolutionCalculate the radius of gyration of a uniform thin rod of mass M and length L about an axis of rotation perpendicular to its length and passing through its centre.
View SolutionCalculate the radius of gyration of a cylindrical rod of mass M and length L about an axis of rotation perpendicular to its length and passing through its centre.
View SolutionA weightless rod of length 2l carries two equal masses 'm' , one secured at lower end A and the other at the middle of the rod at B . The rod can rotate in vertical plane about a fixed horizontal axis passing through C . What horizontal velocity must be imparted to the mass at A so that it just completes the vertical circle.
View SolutionA uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View Solution