A weightless rod of length 2l carries two equal masses 'm' , one secured at lower end A and the other at the middle of the rod at B. The rod can rotate in vertical plane about a fixed horizontal axis passing through C. What horizontal velocity must be imparted to the mass at A so that it just completes the vertical circle.
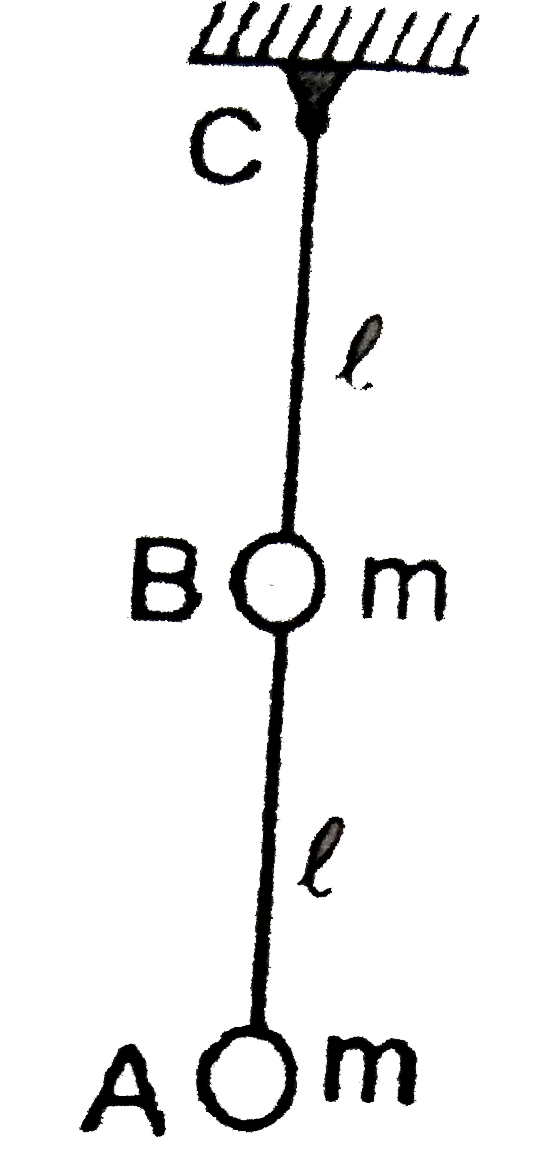
The correct Answer is:u=√485gl
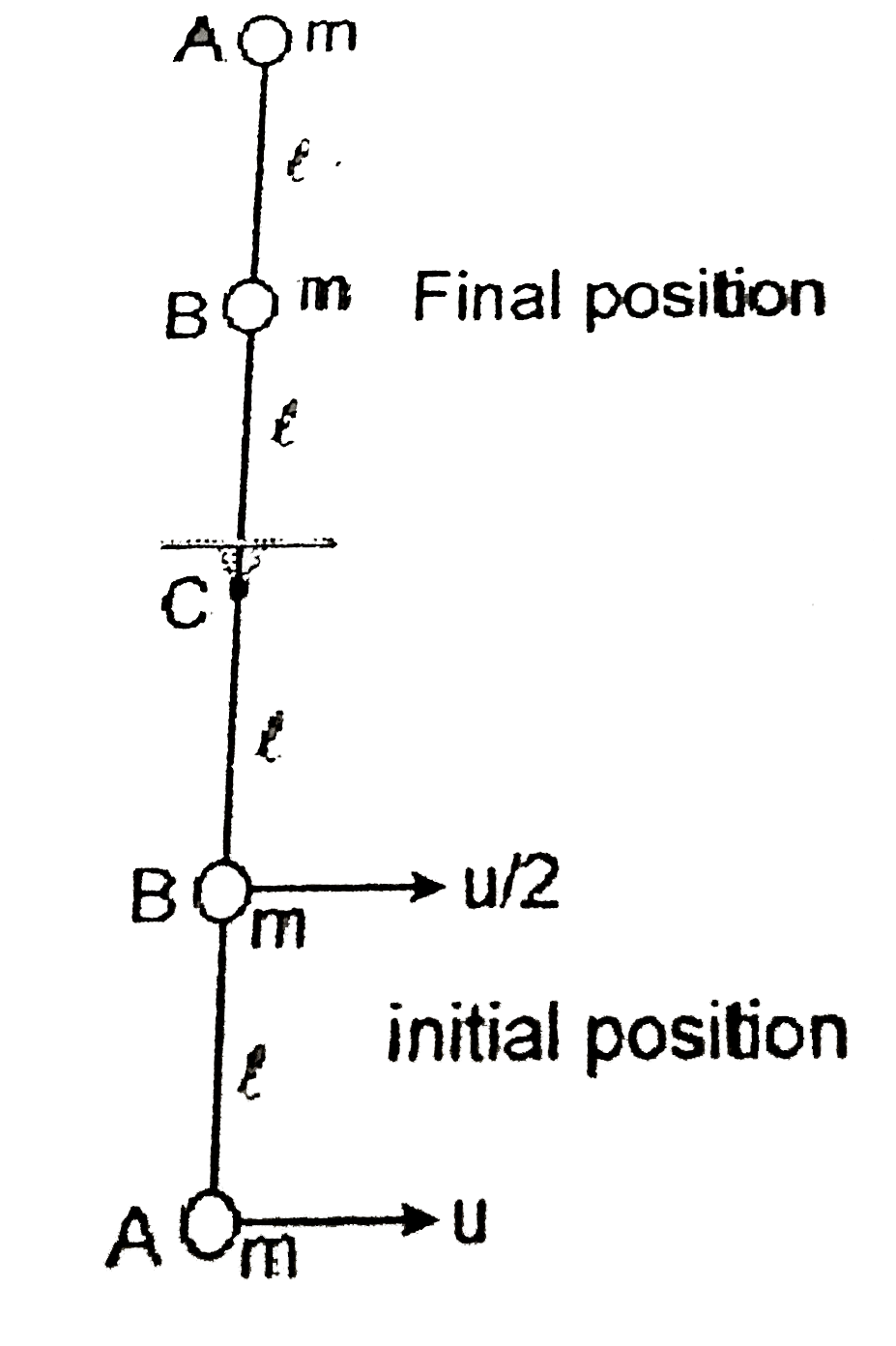
Let the initial given to the mass at A be u. Then the velocity of mass at B is u/2
As the system moves from initial the final position Increase in potential energy is 4ml+2mgl Decrease in kinetic energy.
=12mu2+12m(u2)2=52mu2
From conservation of energy
58mu2=6mloru=√485gl
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 44
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 45
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 42
Explore 7 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
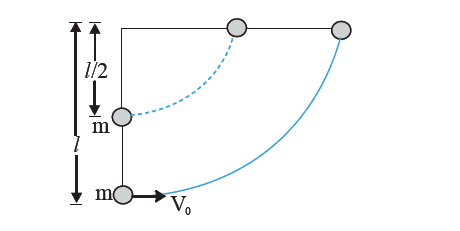
Two point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
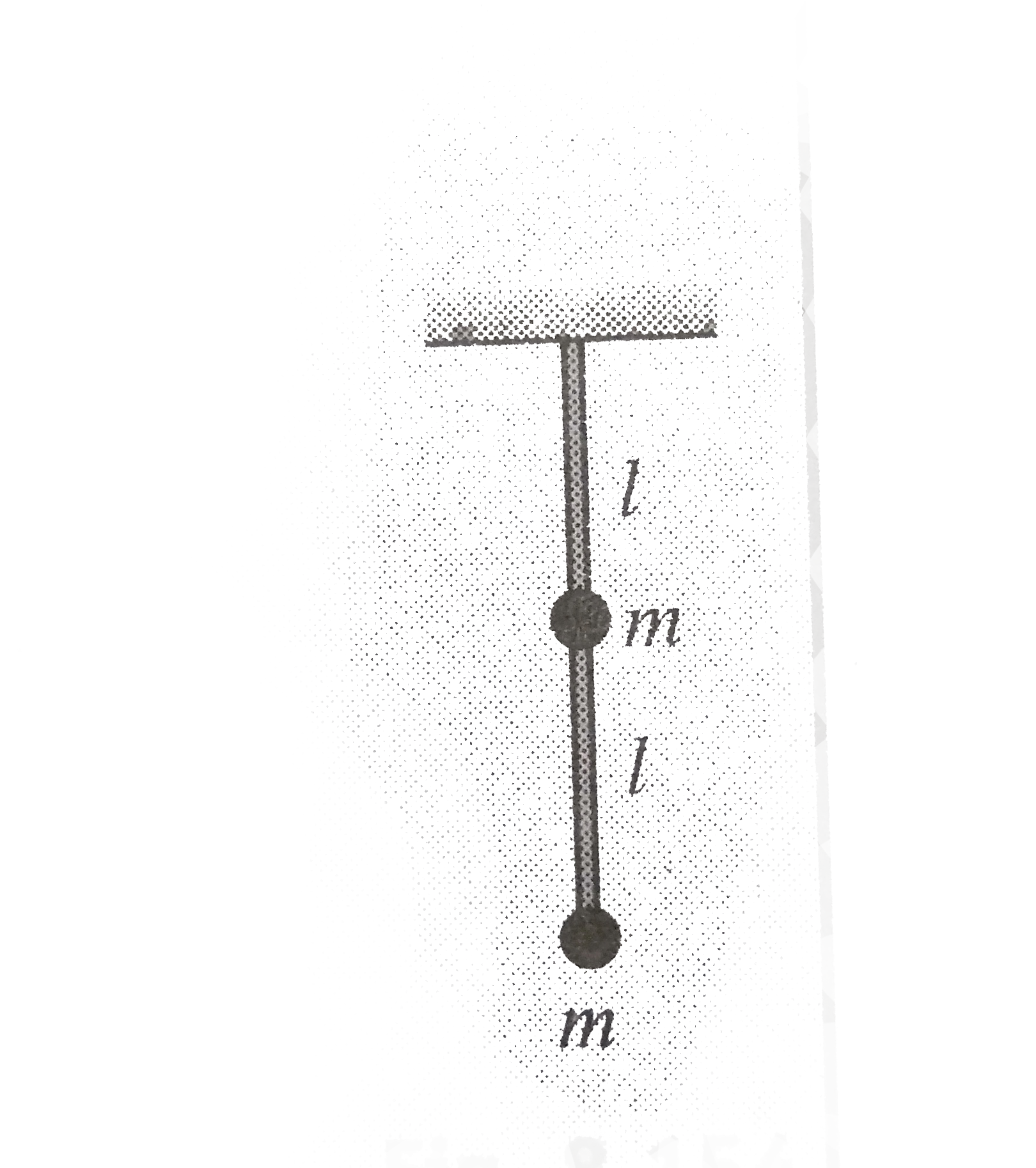
View SolutionA light rod of length l is pivoted at the upper end. Two masses (each m), are attached to the rod, one at the middle and the other at the free end. What horizontal velocity must be imparted to the lower end mass, so that the rod may just take up the horizontal position ?
View Solution
Knowledge Check
A weightless rod of length 2l carries two equal masses 'm', one tied at lower end A and the other at the middle of the rod at B. The rod can rotate in vertical plane about a fixed horizontal axis passing thriugh C . The rod of is released from rest in horizontal possion. The speed of the mass B at the instant rod become vertical is:
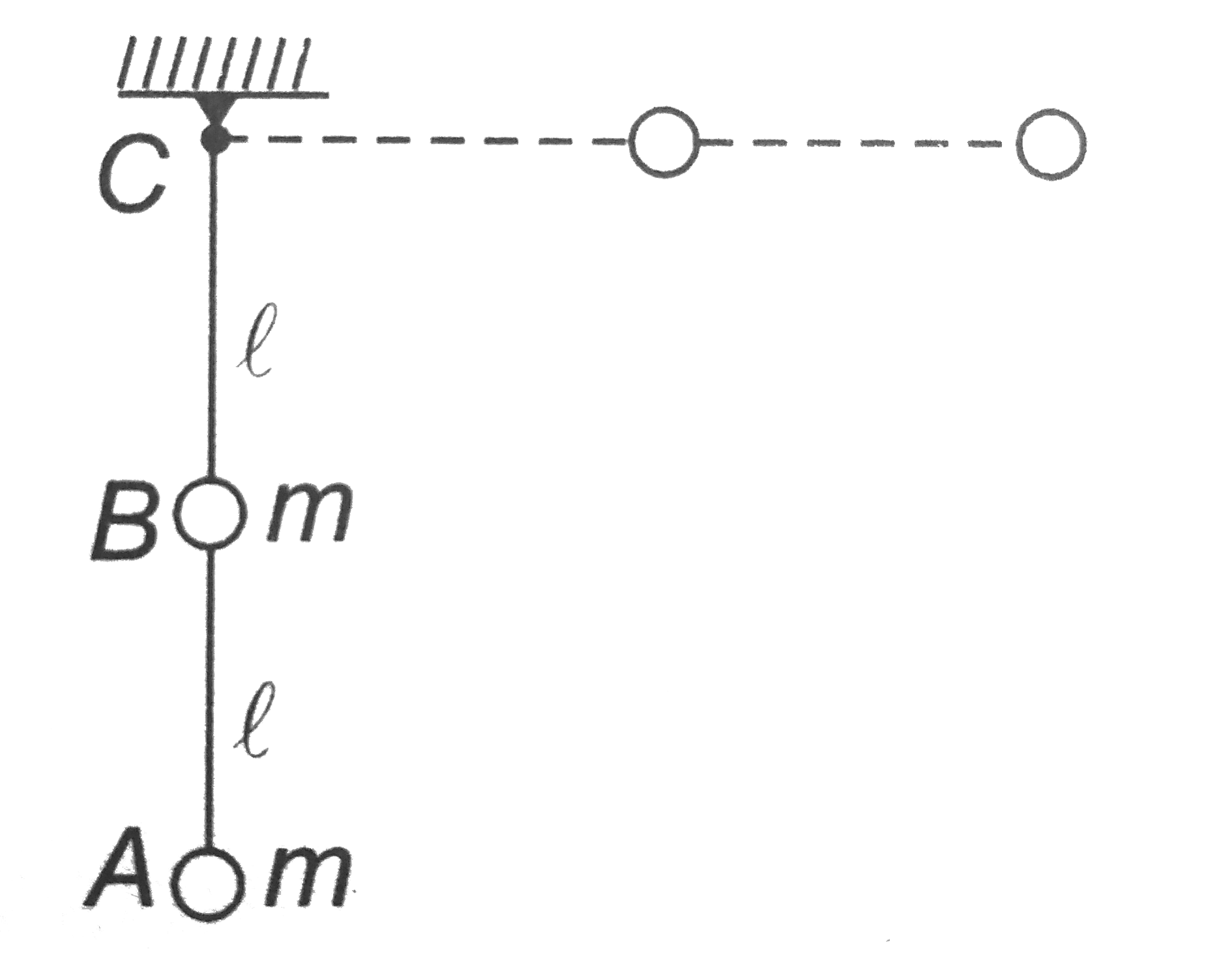 A√3gl5B√4gl5C√6gl5D√7gl5
A√3gl5B√4gl5C√6gl5D√7gl5A weightless rod of length l carries two equal masses m one fixed at the end and other in the middle ofhte rod. The rod can revolve in a vertical plane about A. Then, horizontal velocity which must be imparted to end C of rod to deflect it to horizontal position is
 A√125glB√3glC√165glD√2gl
A√125glB√3glC√165glD√2glA weightless rigid rod AB of length / connects two equal masses m one particle is fixed at the end B and the other at the middle ofthe rod as shown in the figure-5.131. The rod can rotate in the vertical plane freely around the hinge point/4. Choose the correct option(s)
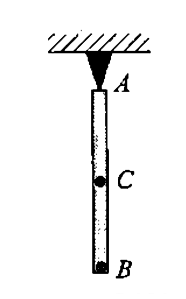 AThe minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circleisBThe minimum horizontal velocity required to begivento the particle B so as to make the rod go around in the complete vertical circle isCThe ratio of compressive force in the rods AC and BC is 2 : 1 when the masses are at highest point.DThe ratio of compressive force in the rodsA
AThe minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circleisBThe minimum horizontal velocity required to begivento the particle B so as to make the rod go around in the complete vertical circle isCThe ratio of compressive force in the rods AC and BC is 2 : 1 when the masses are at highest point.DThe ratio of compressive force in the rodsA
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View SolutionA thin uniform heavy rod of length l hangs from a horizontal axis passing through one end. The initial angular velocity ω that must be imparted to it to rotate it through 90∘ is :
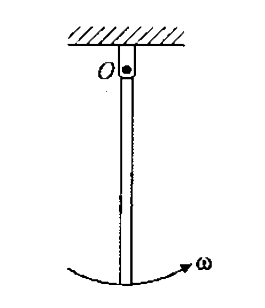
View SolutionA light rod of length l is pivoted at the upper end. Two masses (each m), are attached to the rod, one at the middle and the other at the free end. What horizontal velocity must be imparted to the lower end mass, so that the rod may just take up the horizontal position?

View SolutionA thin uniform rod is free to rotate about a fixed smooth horizontal axis as shown. A point mass hits horizontally with velocity v0 to the one end B of the rod. When it hits, it sticks to the rod, then :

View SolutionA ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?

View Solution

