A thin uniform rod is free to rotate about a fixed smooth horizontal axis as shown. A point mass hits horizontally with velocity v0 to the one end B of the rod. When it hits, it sticks to the rod, then :

Minimum value of v0 for the rod to rotate by an angle π2is2√gL .
Angular acceleration of the rod when the rod is horizontal is 9g8L .
Force applied by the axis on the rod in the horizontal state is 5mg/6 .
for a small velue of v0 the rod performes small oscillations with a period of 43π√lg
The correct Answer is:A, B, C
A thin ………….
(A) Conserving angular momentum about A
mv0L=(mL23+mL2)ω
⇒ω=3v04L
Now, applying energy conservation
12.(4mL2)(3)ω2=mgL+mgL2
Put ω
∴v0=2√gL
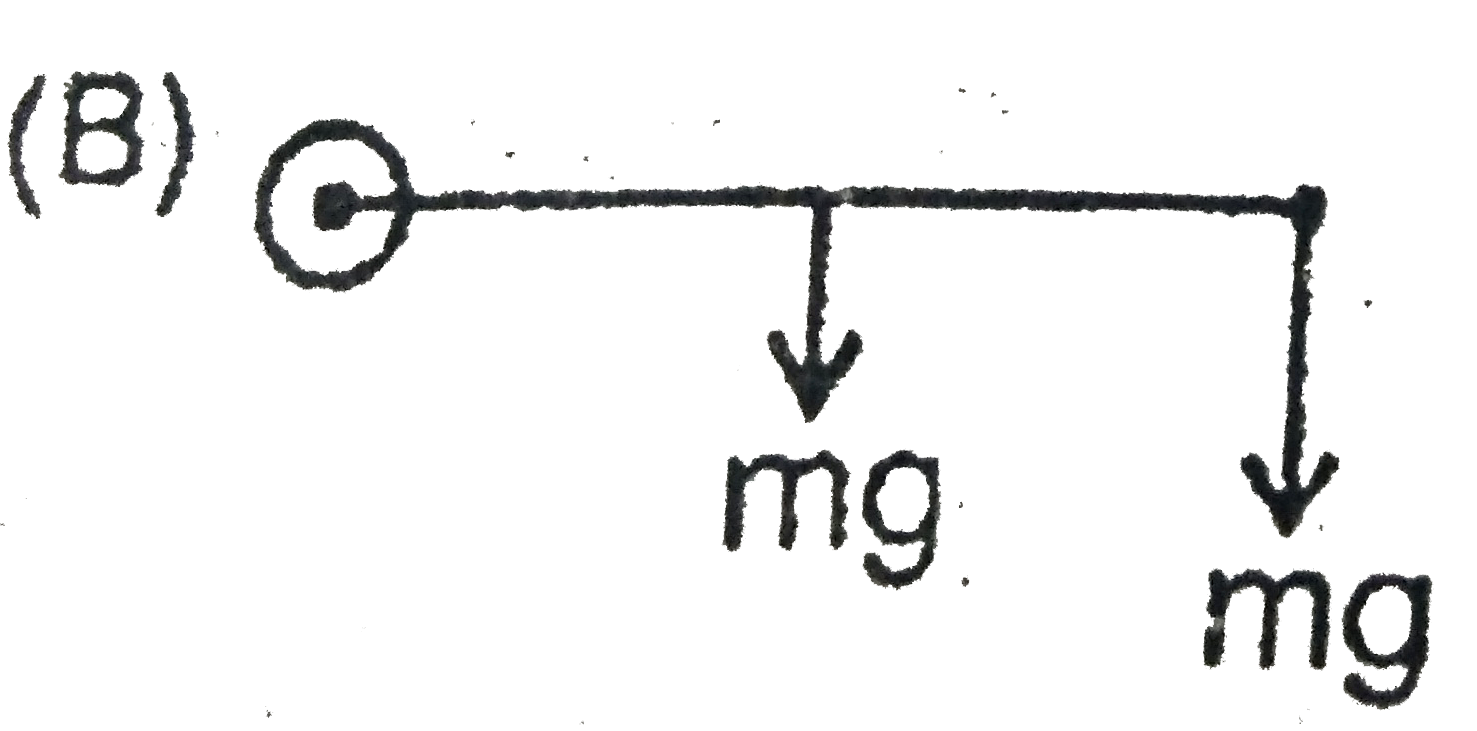
mgL+mgL2=4mL23.α
α=9g8L
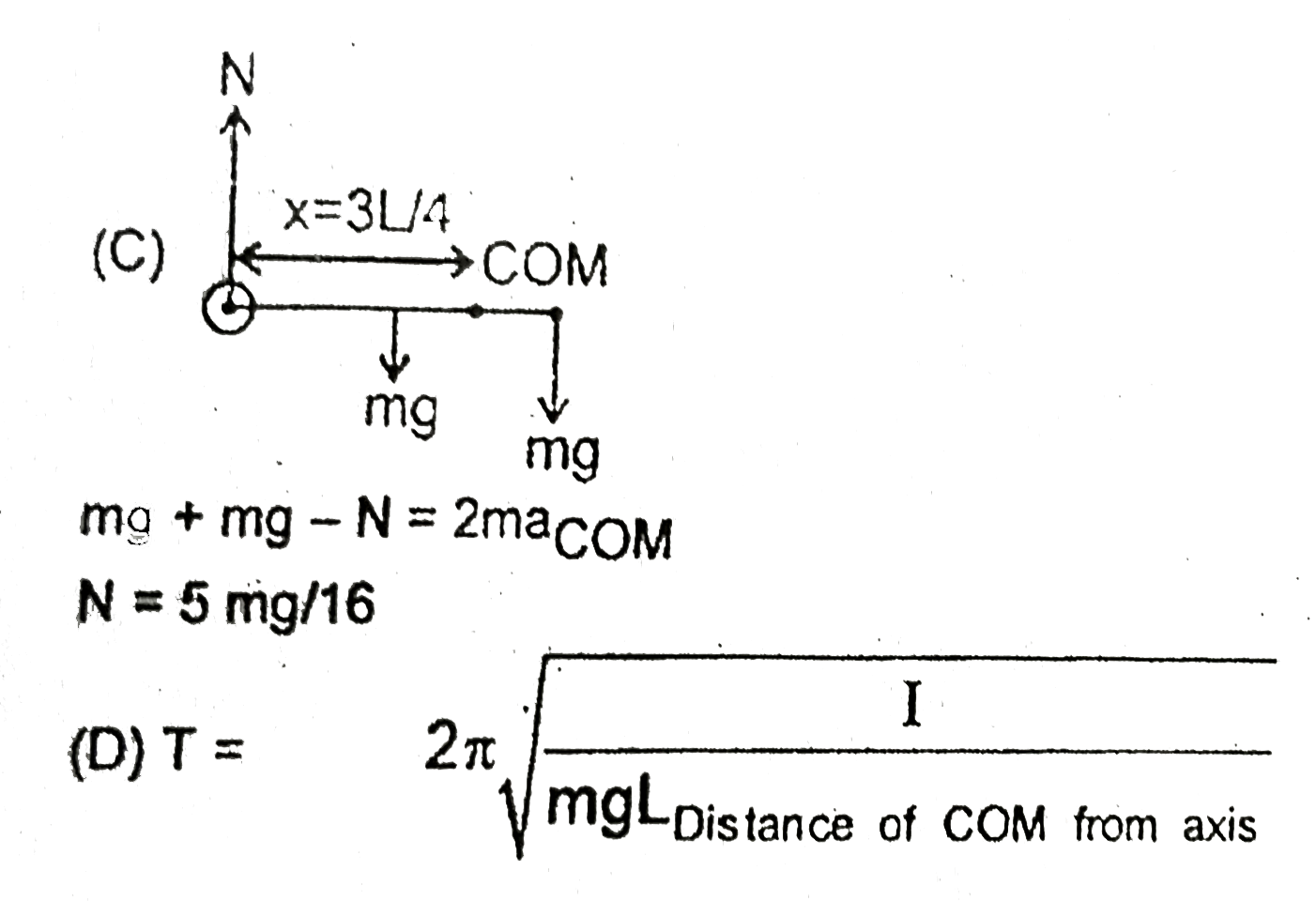
mg+mg−N=2maCOM
N=5mg/16
(D) T=2π√ImgLDistance of COM from axis
23π√2lg
Similar Questions
A uniform rod of length l and mass 2m rest on a smooth horizontal table. A points mass m moving horizontally at right angles to the rod with an initial velocity v collides with one end of the rod and sticks to it.
Determine
(a) the angular velocity of the system after collision,
(b) the position of the point on the rod which remains stationary immediately after collision,
(c) the chabge in kinetic energy of the system as a result of the collision.
View SolutionA thin bar of mass M and length L is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position and then released. The axis is perpendicular to the rod. The angular velocity when it reaches the lowest point is
View Solution
Knowledge Check
A uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
Aangular velocity of the system after collision is vlBangular velocity of the system after collision is v2lCthe loss in kinetic enerlgy of the system as a whole as a result of the collision is mv26Dthe loss in kinetic energy of the system as a whole as a result of the collision is 7mv224A uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
Aangular velocity of the system after collision is 25vlBangular velocity of the system after collision is v2lCThe loss in kinetic energy of the system as a whole as a result of the collision 310mv2DThe loss in kinetic energy of the system as a whole as a result of the collision 7mv224A uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.AThe point is a distance (1/3)l from the end where the mass strikes.BThe point is a distance (2/3)l from the end where the mass strikes.CThe point is a distance (2/5)l from the end where the mass strikesDThe point is a distance(1/5)l from the end where the mass strikes
A uniform rod of mass m and length l is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity v0 collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionA rod of length L whose lower end is fixed along the horizontal plane starts to topple from the vertical position. The velocity of the upper end of the rod when it hits the ground is
View SolutionRod of m and length l is free to rotate about point U in vertical plane. A particle having same mass m moving horizontally with velocity v0 his the rod perpendicular at distance l4 from the top end 'O' and stops. Find impulse due to hinge on the rod due to collision.
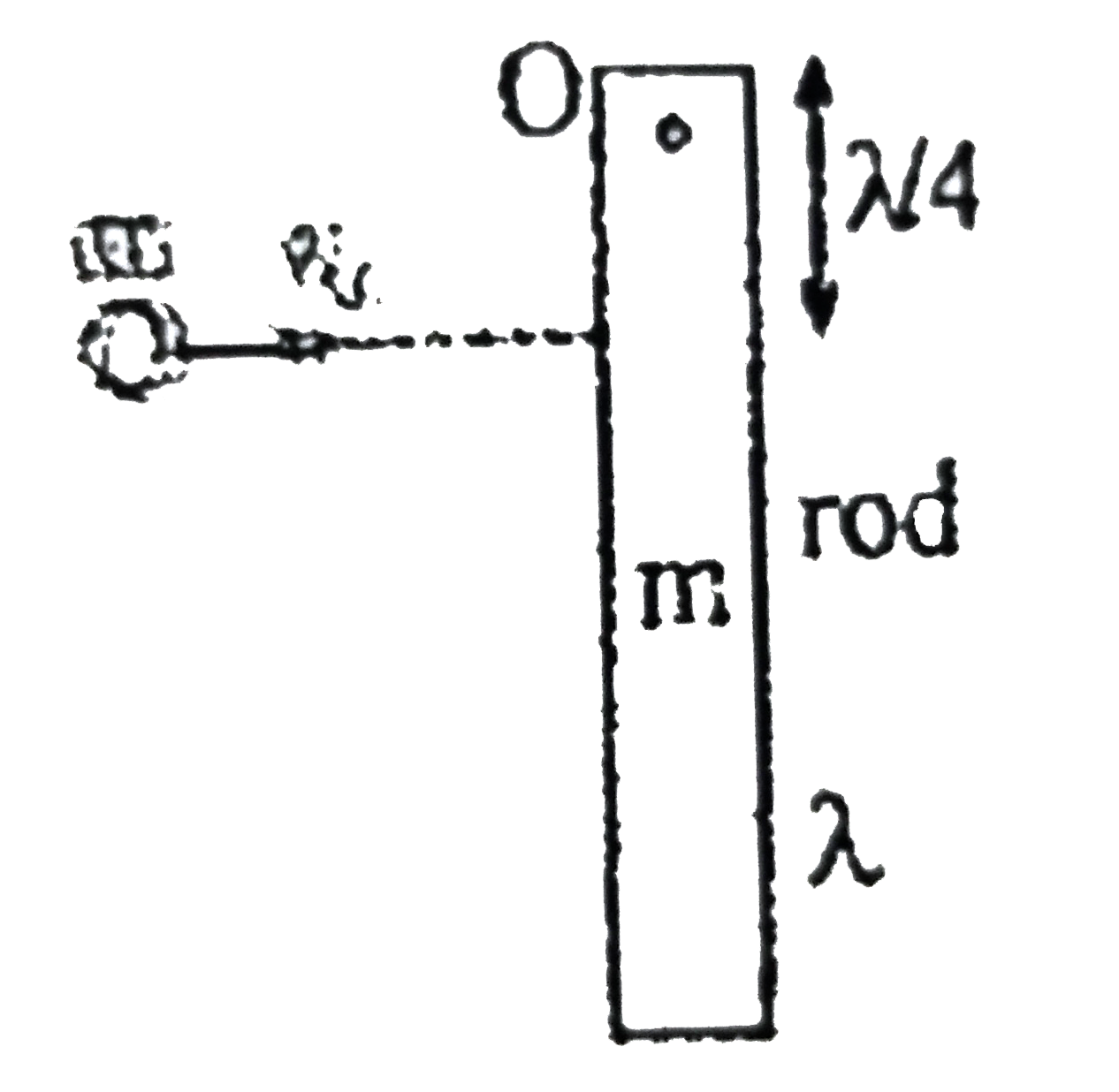
View SolutionA uniform rod is resting freely over a smooth horizontal plane. A particle moving horizontally strikes at one end of the rod normally and gets stuck. Then
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View Solution
