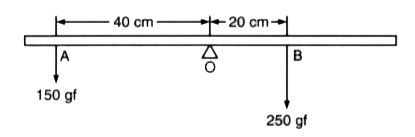
The diagram in Fig 1.38 shows a uniform metre rule weighing 100gf pivoted as its centre O. two weights 150 gf and 250 gf hang from the metre rule as shown.Calculate:i the total anticlockwise moment about o ii the total clockwise moment about O iii the difference of anticlockwise and clockwise moments andiv the distance from O where a 100 gf weight should be placed to balance the metre rule.
i Total anticlockwise moment about O= 150 gf × 40 cm = 6000 gf cmii Total clockwise moment about O = 250gf × 20 cm = 5000 gf cmiii The difference of anticlockwise and clockwise moment = 6000 – 5000 = 1000gf cmiv From the principle of moments Anticlockwise moment = Clockwise moment To balance it 100gf weight should be kept on right hand side so as to produce a clockwise moment about the O. Let its distance from the point O be d cm. Then 150gf × 40 cm = 250gf × 20 cm + 100gf × d6000gf cm = 5000gf cm + 100gf × d1000gf cm = 100 gf × dSo d= 1000gf cm/100gf= 10 cm on the right side of O.
Related Solutions
The diagram in Fig.1.34 shows a uniform metre rule weighing 100gf, pivoted at its centre O. Two weights 150 gf and 250 gf hang from the points A and B respectively of the metre rule such that OA= 40cm and OB=20cm . Calculate (i) the total anticlockwise moment about O, (ii) the total clockwise moment about O, (iii) the difference of anticlockwise and clockwise moments, and (iv) the distance from O where a 100gf weight should be placed to balanced the metre rule.
View SolutionA uniform metre rule is pivoted at its mid-point. A weight of 50 gf is suspended at one end. Where should be a weight of 100 gf suspended to keep the rule horizontal?
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find: the position of another weight of 50 gf to balance the rule in part (ii).
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
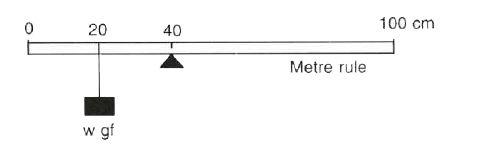
the value of w.
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
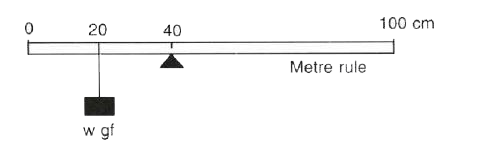
the resultant moment and its direction if the weight w is moved to the mark 30 cm.
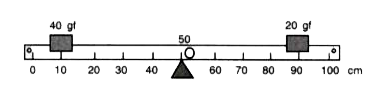
View SolutionFig.1.33 shows a uniform metre rule placed on a fulcrum at its mid point O and having a weight 40gf at the 10cm mark and a weight of 20gf at the 90cm mark. (i) Is the metre rule in equilibrium? If not , how will the turn?
(ii) How can the rule be brought in equilibrium by using an additional weight of 40 gf?
View SolutionA half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below.
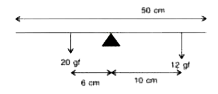
Which of the two forces acting on the rigid rod causes clockwise moment?
View SolutionA uniform metre scale of weight 20 gf is supported on a wedge placed at 60 cm mark. If a weight of 30 gf is suspended at 15 cm mark, where should a weight 200 gf be suspended in order to balance the metre scale?
View SolutionA uniform metre rule is pivoted as its mid point. A weight of 50gf is suspended at one end of it. Where should a weight of 100gf be suspended to keep the rule horizontal?
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end. What is the weight of the half metre rule ?
View SolutionA half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below:
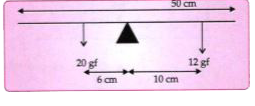
Is the rod in equilibrium ?
View SolutionA uniform metre rod is balanced at the 70 cm mark by suspending a weight of 50 gf at the 40 cm mark and 200 gf at the 95 cm mark. Draw a diagram of the arrangement and calculate the weight of the metre rod.
View SolutionA half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below: The direction of 20 kgf force is reversed. What is the magnitude of the resultant moment of the forces on the rod ?
View SolutionThe moment of force in clockwise direction is _________ the moment in the anticlockwise direction.
View SolutionBy convention, the clockwise moments are taken as ………………………………. and the anticlockwise moments are taken as ……………………………….
View SolutionBy convention , the clockwise moments are taken as __________ and the anticlockwise moments are taken as __________.
View SolutionBy convention, the clockwise moments are taken as ________ and the anticlockwise moments are taken as ____________.
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
Draw a diagram of the arrangement.
View SolutionThe algebraic sum of the moments in the clockwise direction is ________ to the algebraic sum moments in the anticlockwise .
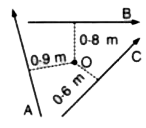
View SolutionA, B and C are three forces each of magnitude 4N acting in the plane of paper as shown in fig.1.26 Point O lies in the same plane.
(i) Which force has the least moment about O? Give reason.
(ii) Which force has the greatest moment about O? Give reason.
(iii) Name the forces producing (a) clockwise , (b) anticlockwise moments.
(iv) What is the resultant torque about the point O?
View Solution