In Fig. 12.11 the feasible region shaded for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y
Hence the maximum and minimum value of Z are 9 and 22/7 respectively.
Related Solutions
In the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of
View SolutionThe feasible region for an LPP is shown shaded in the figure 12.47. Determine the maximum and minimum values of Z=x+2y.
View SolutionIn the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y

View SolutionIn Figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of z = x + 2y.
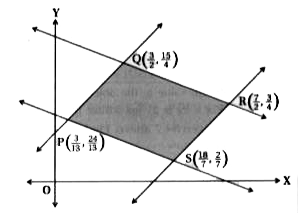
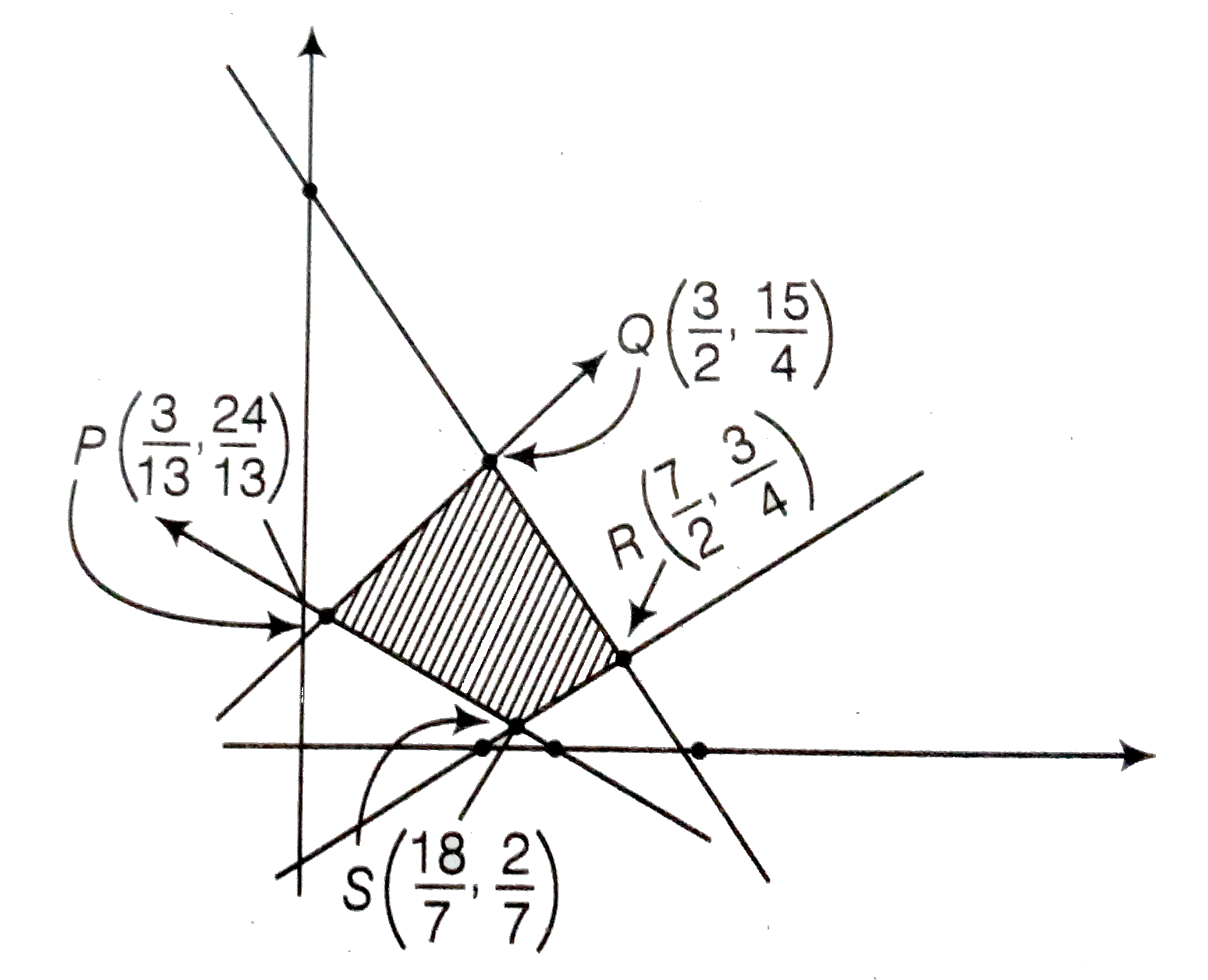
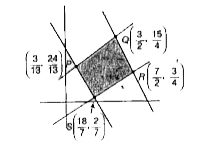
View SolutionIn the following figure, the feasible region for a LPP is shown.
Determine the maximum and minimum value of
.
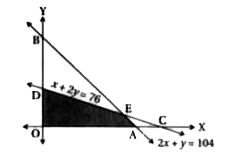
View SolutionDetermine the maximum value of z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure.
View SolutionDetermine the maximum value of z = 4x + 3y if the feasible region for an LPP is
shown shaded in the figure
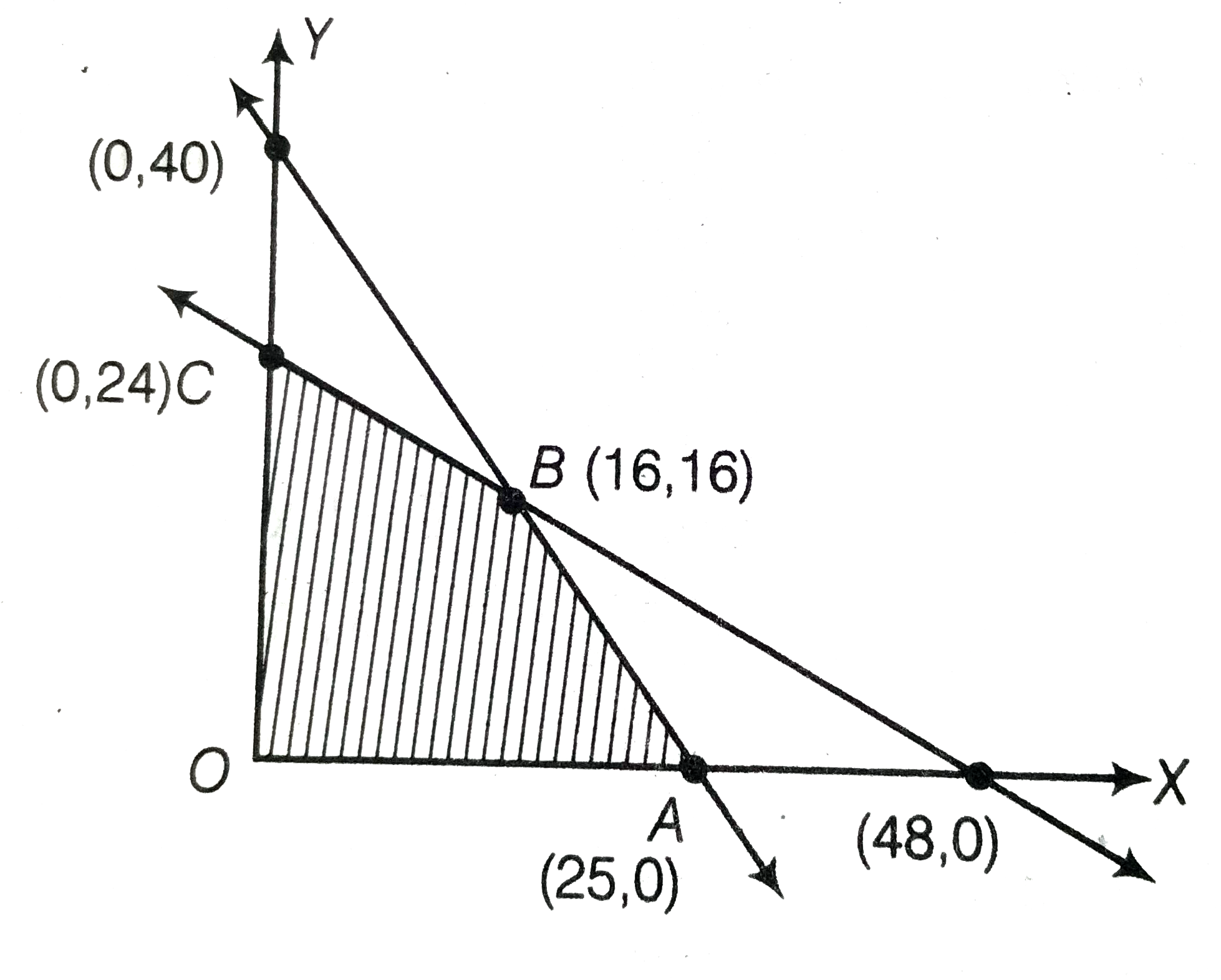
View SolutionThe feasible region (shaded) of an LLP is shown in the figure. Find the maximum and minimum values of Z = x + 2y.
View SolutionDetermine the minimum value of (if any), if the feasible region for an LPP is shown in figure:
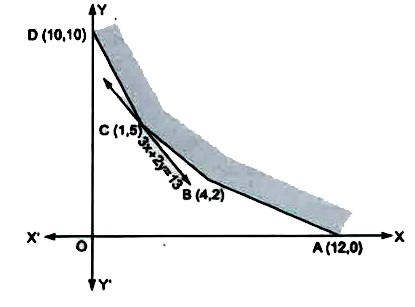
View SolutionThe feasible region for LPP is shown shaded in the figure . Find the minimum value of the objective function z = 11x + 7y.
View SolutionThe feasible region for an LPP is shown shaded in the figure 12.48 find the minimum value of Z=4x+y.
View SolutionFeasible region (shaded) for a LPP is shown in Figure Maximise z = 5x + 7y.
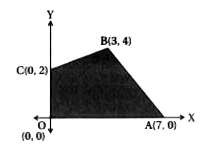
View SolutionDetermine the maximum value of Z=3x+4y, if the feasible reigon (shaded) for a LPP is shown in following figure
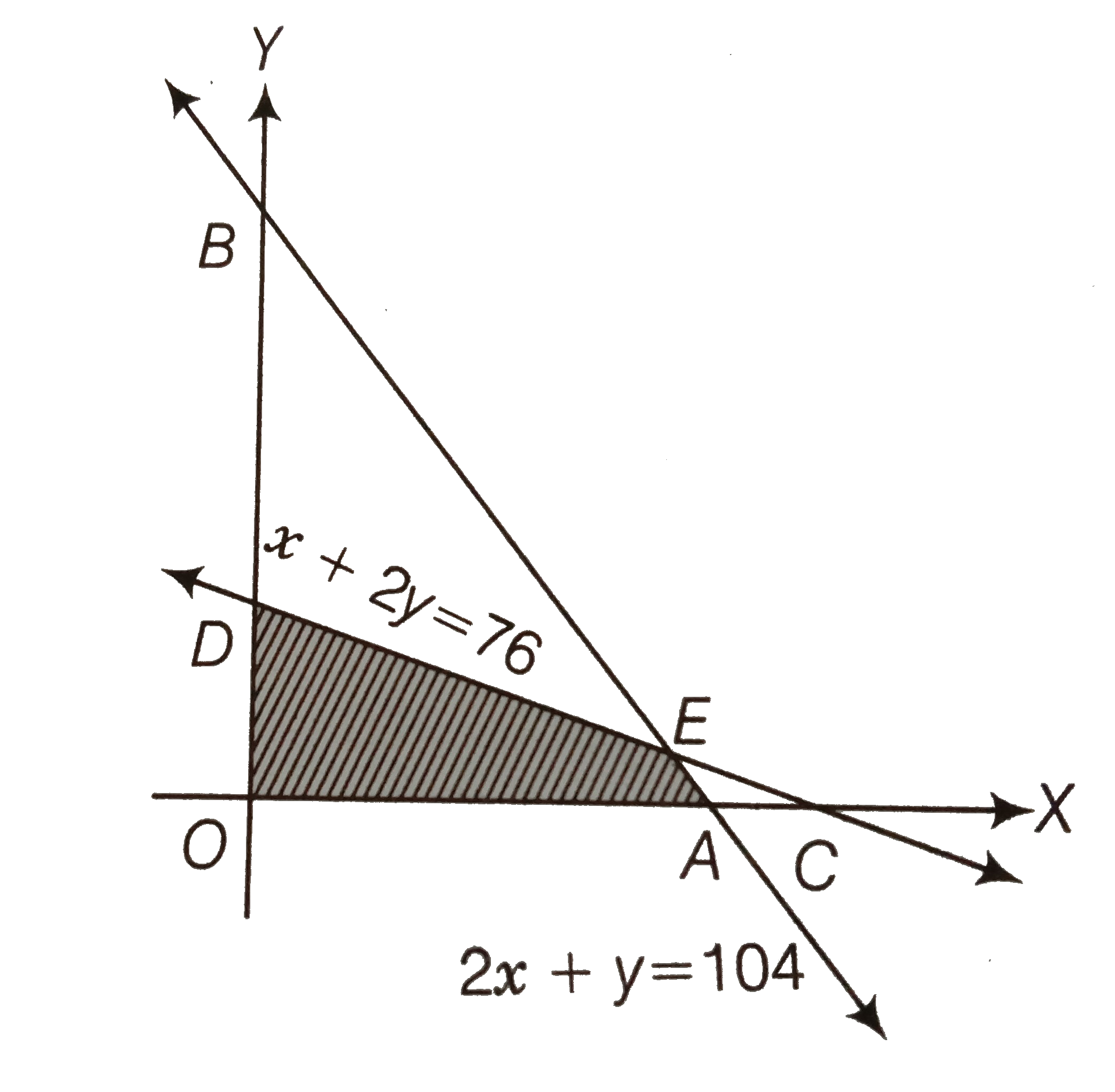
View SolutionDetermine the maximum value of Z=3x+4y, if the feasible reigon (shaded) for a LPP is shown in following figure

View SolutionDetermine the minimum value of ( if any) , if the feasible region for an LPP is ashown in the figure:
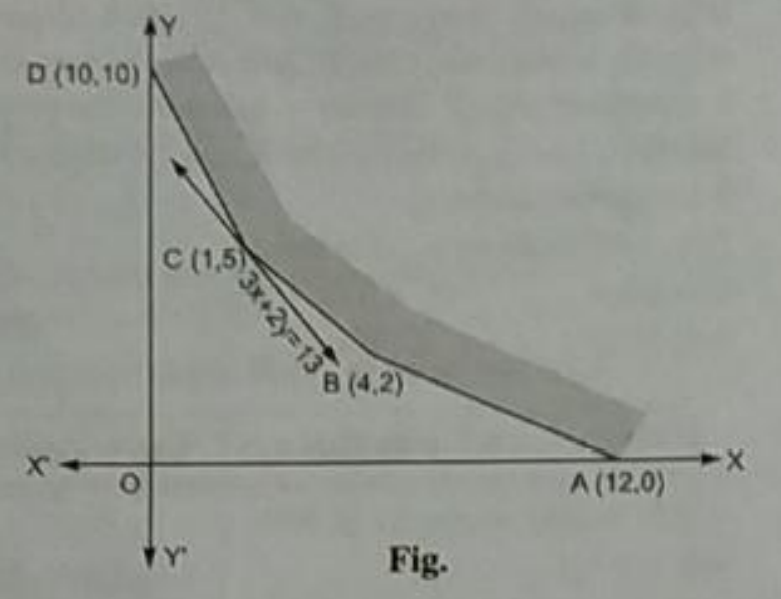
View SolutionIn the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
View SolutionFeasible region (shaded ) for a LPP is shown in the following figure
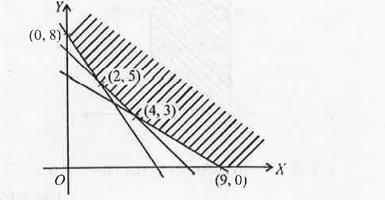
View SolutionDetermine the minimum value of Z=3x+2y, if the feasible region is show shaded in the figure 12.44.
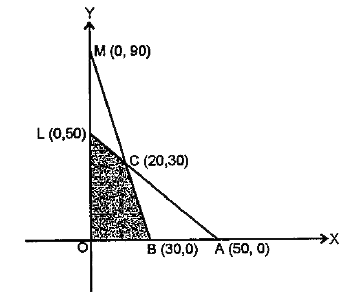
View SolutionThe feasible solution for a LPP is shown in Fig. Let be the objective function. Maximum value of Z is 130.
View Solution