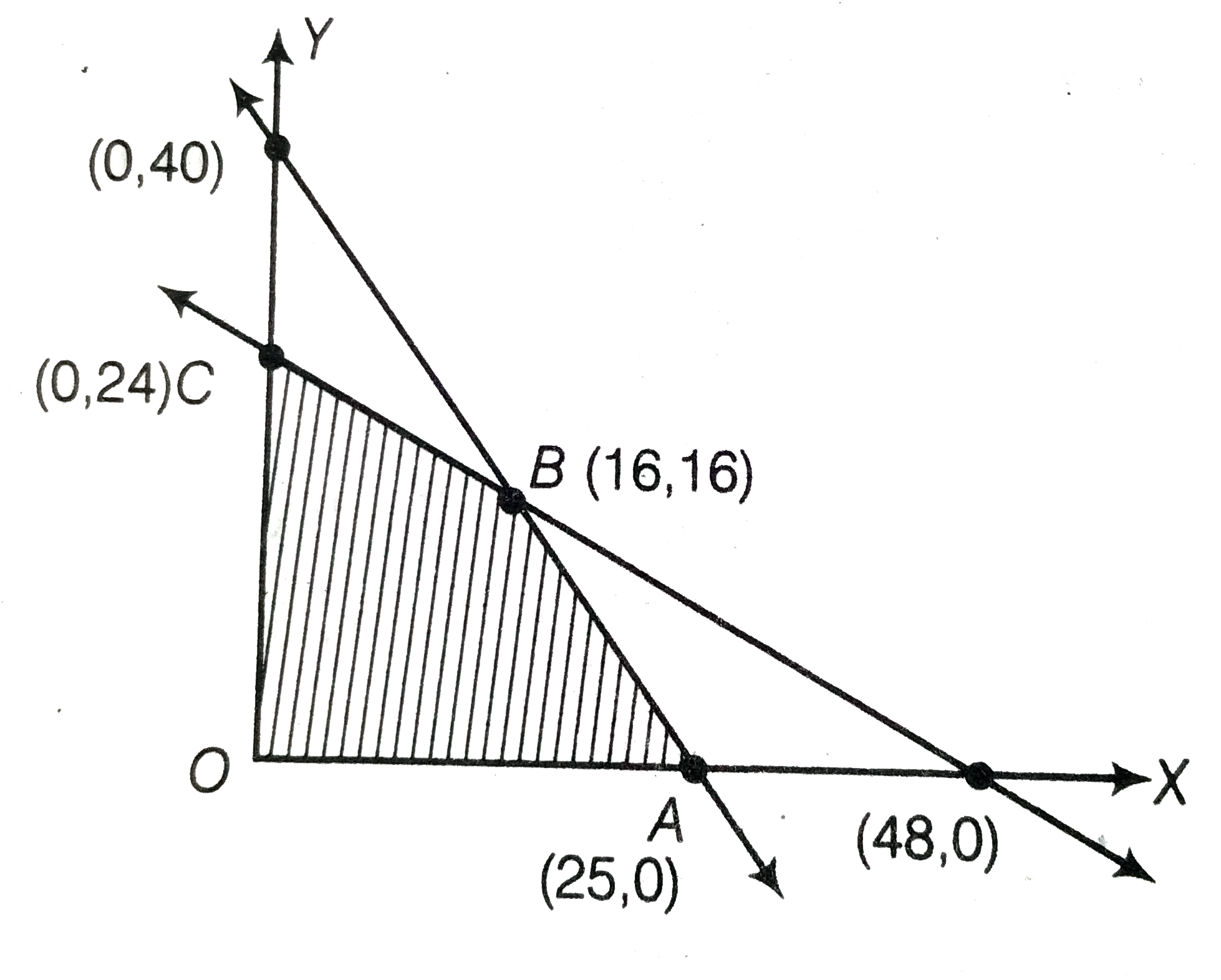
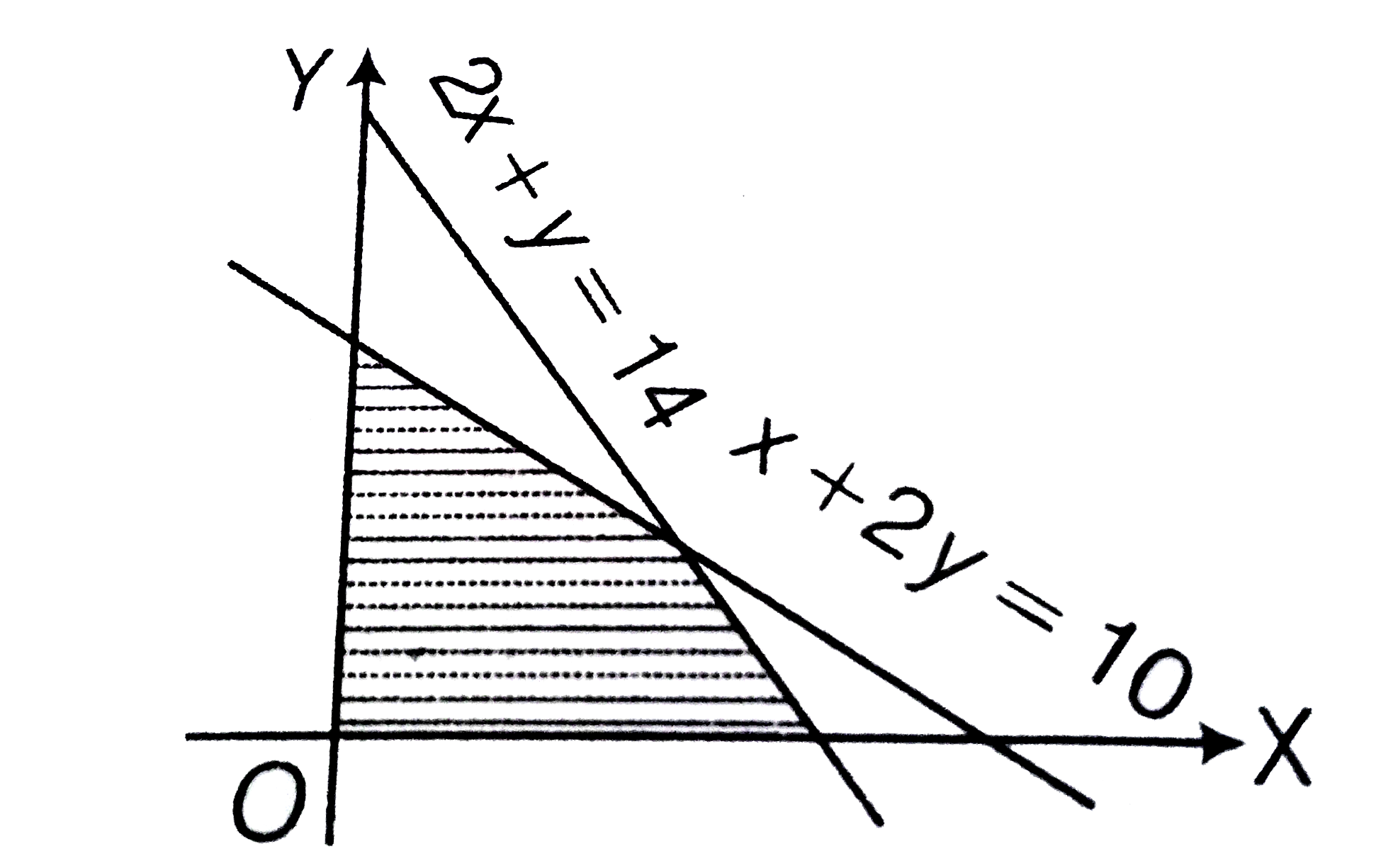
Determine the minimum value of Z=3x+2y (if any), if the feasible region for an LPP is shown in figure:
Minimum value of Z = 11.
Minimum value of Z = 14.
Minimum value of Z = 12.
Minimum value of Z = 13.
The correct Answer is:D
Step by step video, text & image solution for Determine the minimum value of Z = 3x + 2y (if any), if the feasible region for an LPP is shown in figure: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - FAQs
9 Videos
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - (FAQ)
18 Videos
- INVERSE - TRIGONOMETRIC FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - INVERSE - TRIGONOMETRIC FUNCTIONSEXERCISE - CHAPTER TEST (2)
11 Videos
- MATRICESBOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - CHAPTER TEST (3)
12 Videos
Similar Questions
Knowledge Check
The corner point method for bounded feasible region comprises of the following steps
I. When the feasible region is bounded, M and m are the maximum and minimum values of Z.
II. Find the feasible region of the linear programming problem and determine its corner points.
Ill. Evaluate the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values of these points.
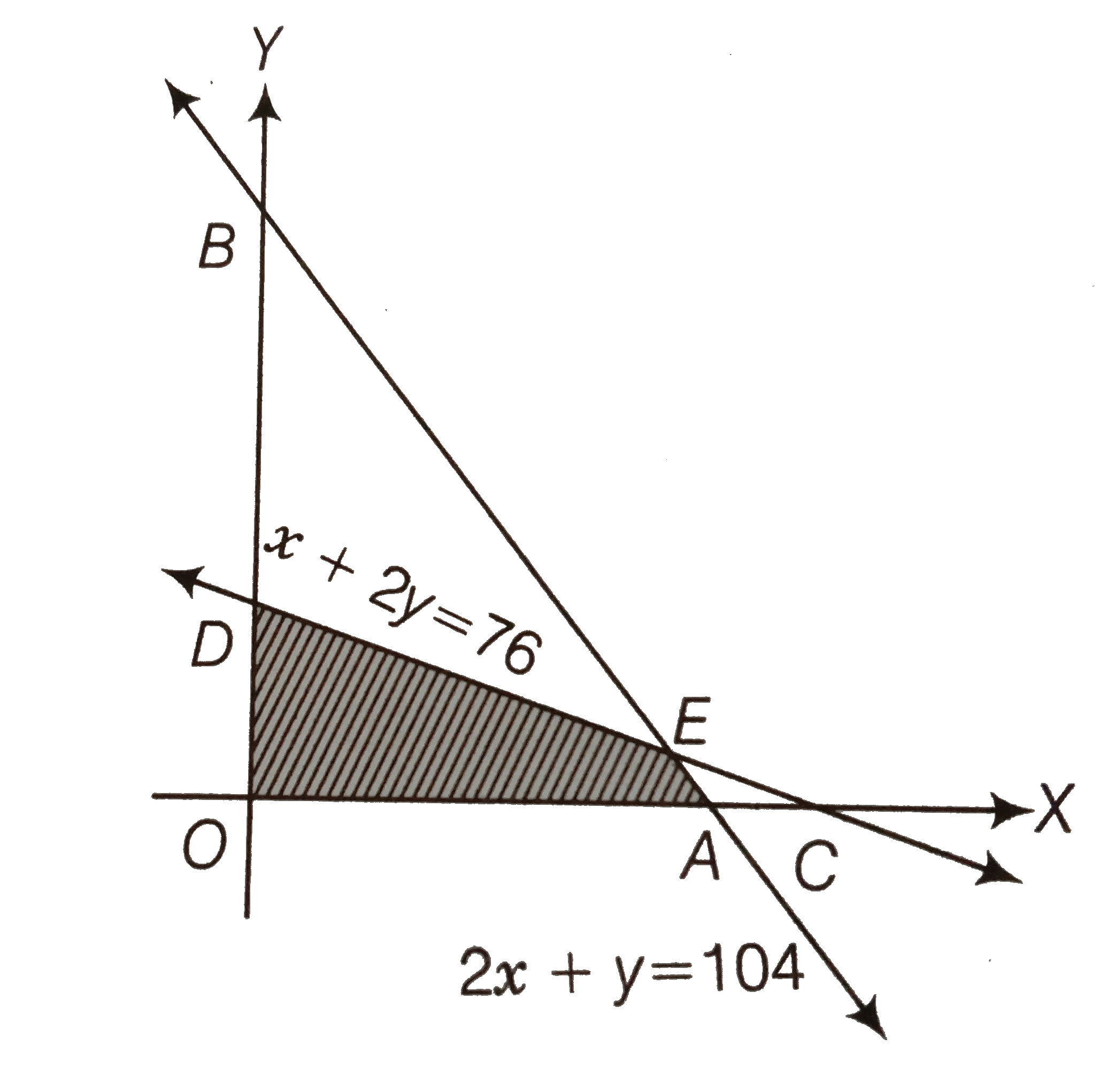
The correct order of these above steps isAIII,I,IIBII,III,ICII,I,IIIDI,III,IIThe feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.
 A22B23C24D21
A22B23C24D21Consider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IV
Find the maximum value of f(x,y)=3x+8y in following feasible region:
View SolutionThe maximum value of objective function Z=3x+y under given feasible region is
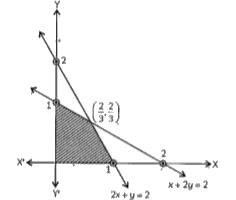
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
View SolutionFeasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.

View SolutionIn a LPP, if the objective function Z=ax+by has the same maximum value of two corner points of the feasible region, then every point of the line segment joining these two points give the same ..value.
View Solution