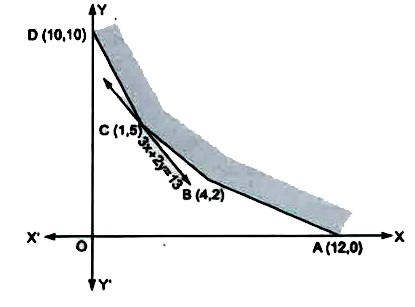
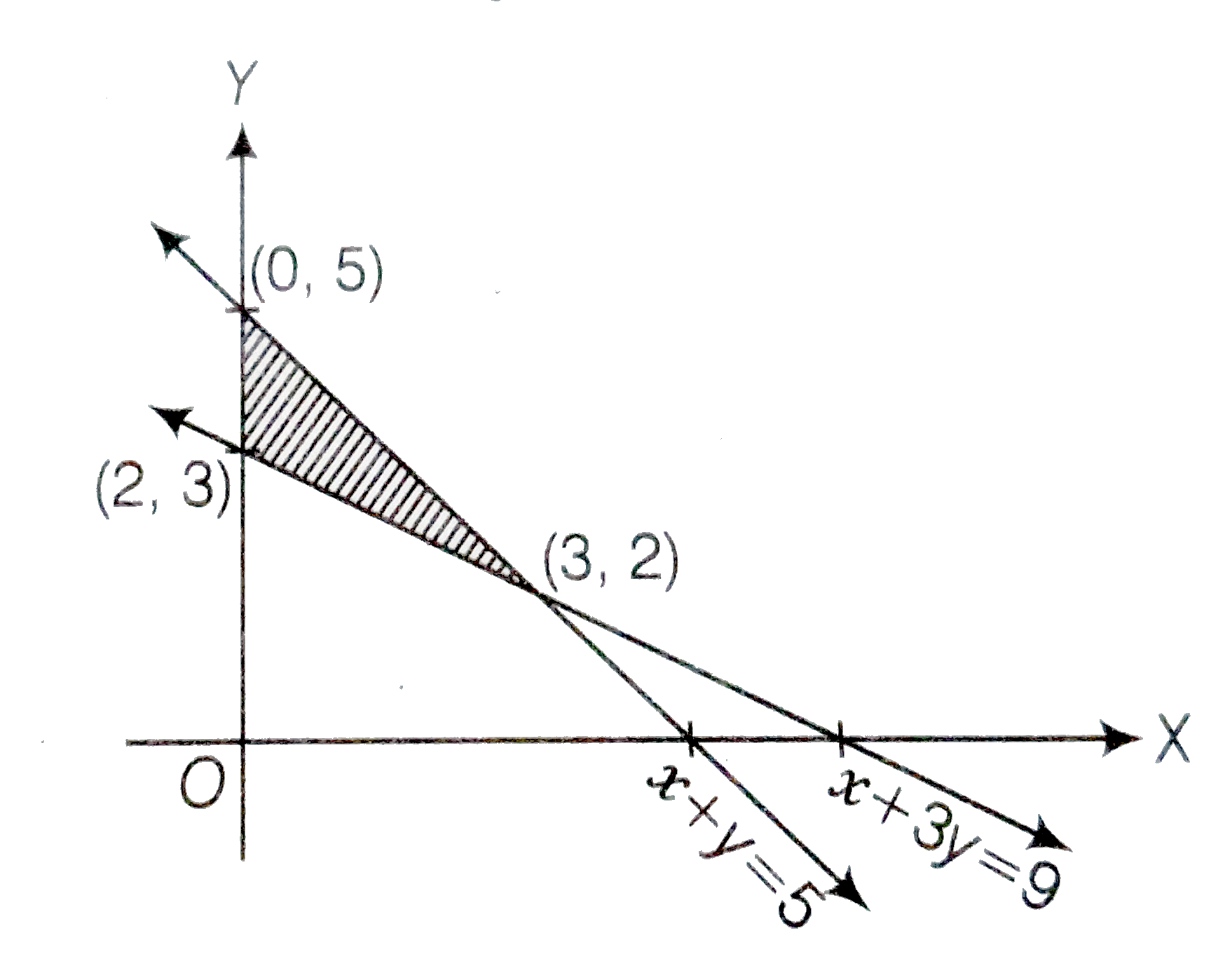
Determine the minimum value of Z = 3x + 2y if any if the feasible region for an LPP is shown in Fig.12.2.
The feasible region R is unbounded. Therefore minimum of Z may or may not exist. If it exists it will be at the corner point Fig.12.2.Let us graph 3x + 2y < 13. We see that the open half plane determined by 3x + 2y < 13 and R do not have a common point. So the smallest value 13 is the minimum value of Z.
Related Solutions
Determine the minimum value of (if any), if the feasible region for an LPP is shown in figure:
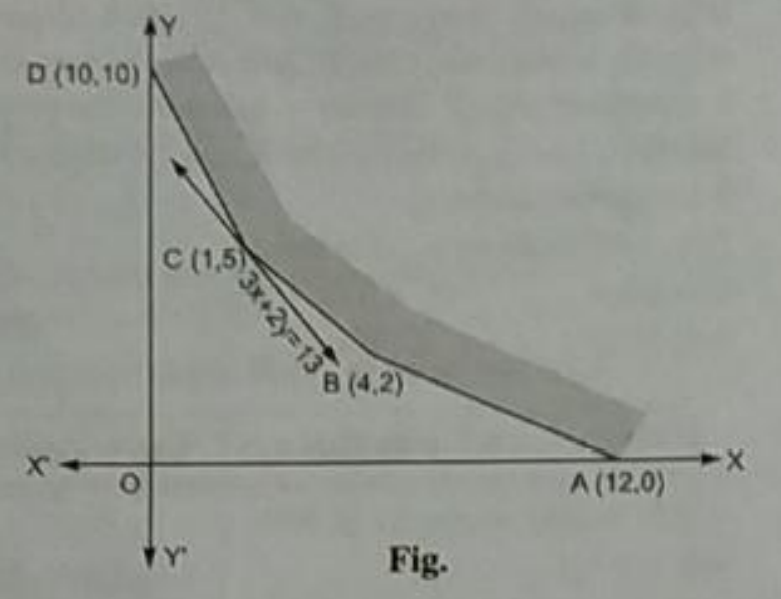
View SolutionDetermine the minimum value of ( if any) , if the feasible region for an LPP is ashown in the figure:
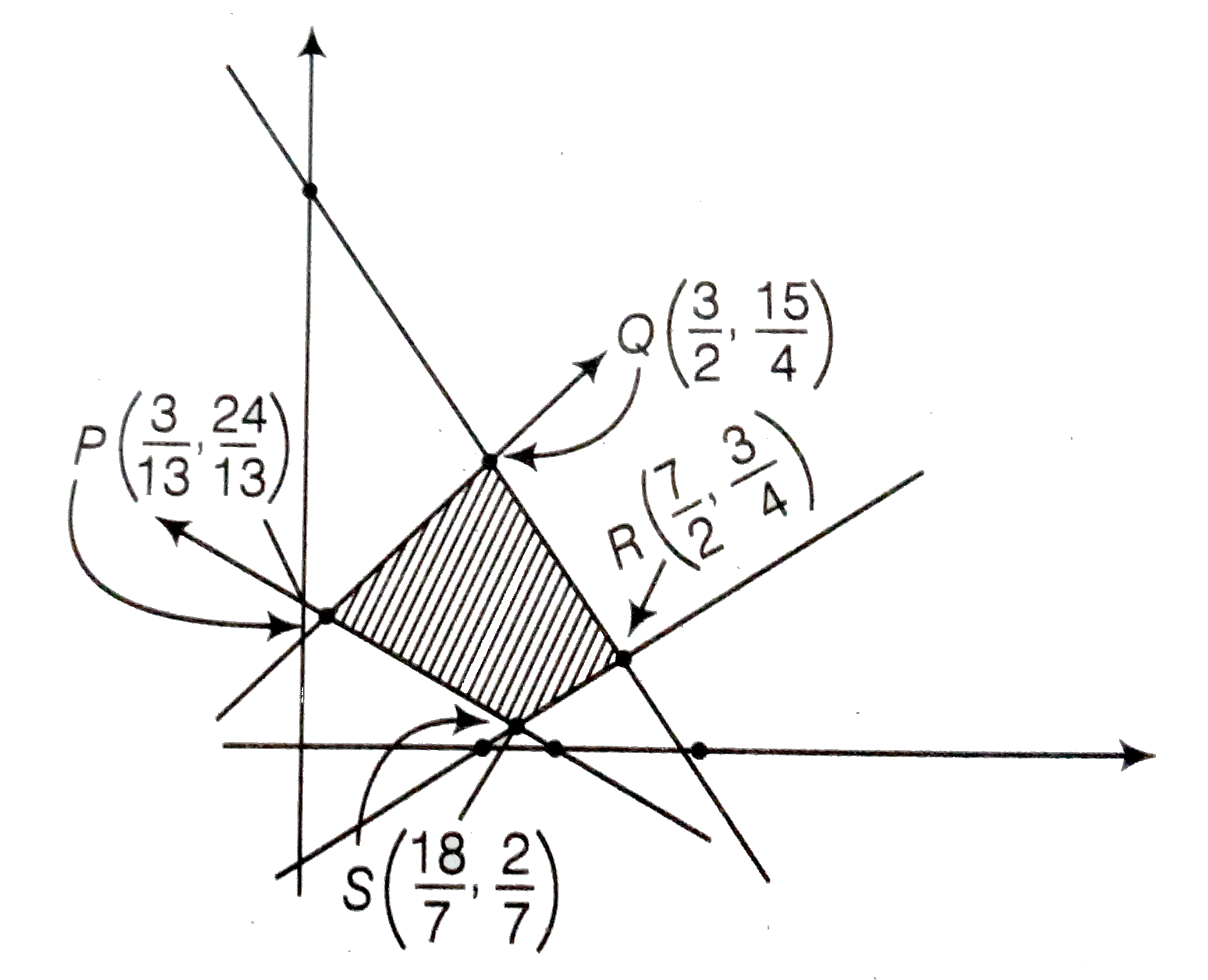
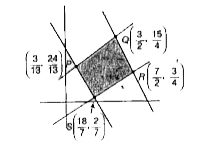
View SolutionIn the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of
View SolutionThe feasible region for an LPP is shown shaded in the figure 12.47. Determine the maximum and minimum values of Z=x+2y.
View SolutionIn the following figure, the feasible region for a LPP is shown.
Determine the maximum and minimum value of
.
View SolutionIn the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y

View SolutionIn Figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of z = x + 2y.
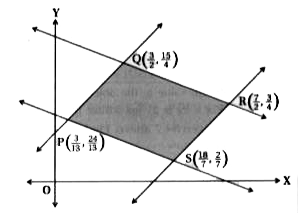
View SolutionThe feasible region of an LPP is shown in the figure. If z = 3x + 9 y , then the minimum value of z occurs at
View SolutionThe feasible region of an LPP is shown in the figure. If ,then the minimum value of z occurs at
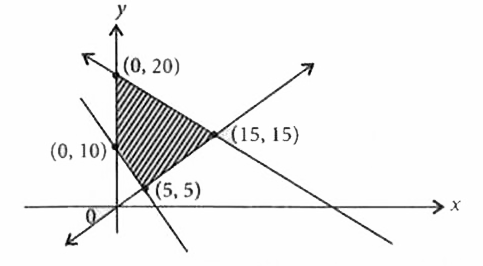
View SolutionThe feasible solution for a LPP is shown in Fig. Let. Z = 3x-4 y be the objective function. Minimum value of F is
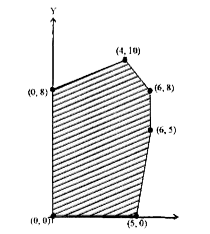
View SolutionDetermine the maximum value of z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure.
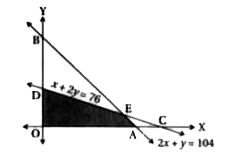
View SolutionThe feasible solution for a LPP is shown in Fig. Let, Z=3x-4 y be the objective function. (Maximum value of Z+ Minimum value of Z) is equal to :
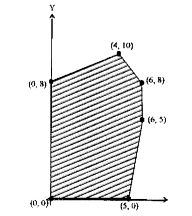
View SolutionThe feasible solution for a LPP is shown in Fig. Let. Z = 3x - 4 y be the objective function. Minimum of Z occurs at
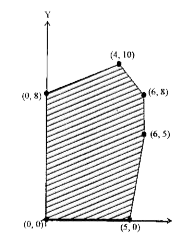
View SolutionThe feasible region of an Lpp is shown in the figure. If z= 3x+9y, then the minimum variable occurs at
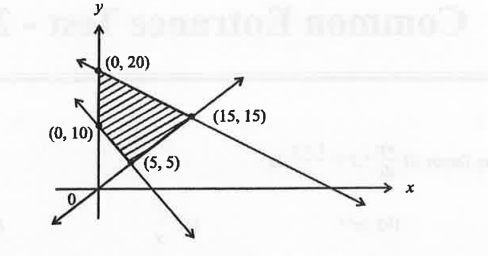
View SolutionDetermine the minimum value of Z=3x+2y, if the feasible region is show shaded in the figure 12.44.
View SolutionThe feasible region for a LPP is shown in Figure. Find the minimum value of .
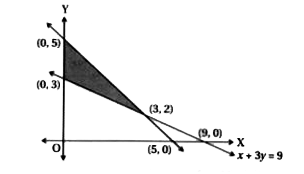
View SolutionThe feasible region for LPP is shown shaded in the figure . Find the minimum value of the objective function z = 11x + 7y.
View SolutionThe feasible region for an LPP is shown shaded in the figure 12.48 find the minimum value of Z=4x+y.
View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of
View Solution