The springs of spring factor k 2k k respectively are connected in parallel to a mass m. If the mass = 0.08kg m and k = 2N|m then find the new time period?
Total spring constant
Related Solutions
The time period of a spring mass system of spring constant k and mass m is T. Now, the spring is cut into two equal parts and connected in parallel. If the same mass is attached to new arrangement, then new time period is
View Solutionk तथा 2k बल नियतांक वाली दो स्प्रिंगें, द्रव्यमान m से चित्रानुसार जुड़ी हैं। द्रव्यमान m के दोलनों की आवृत्ति है
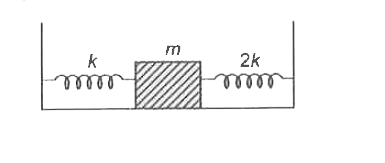
View SolutionTwo identical springs are connected to mass m as shown (k= spring constant) If the period of the configuration in (a) is 2S , the period of the configuration (b) is
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
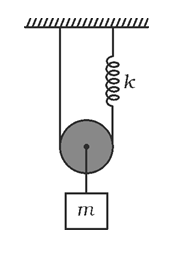
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
View SolutionTwo spring of force constants and are connected a mass below The frequency of oscillation the mass is
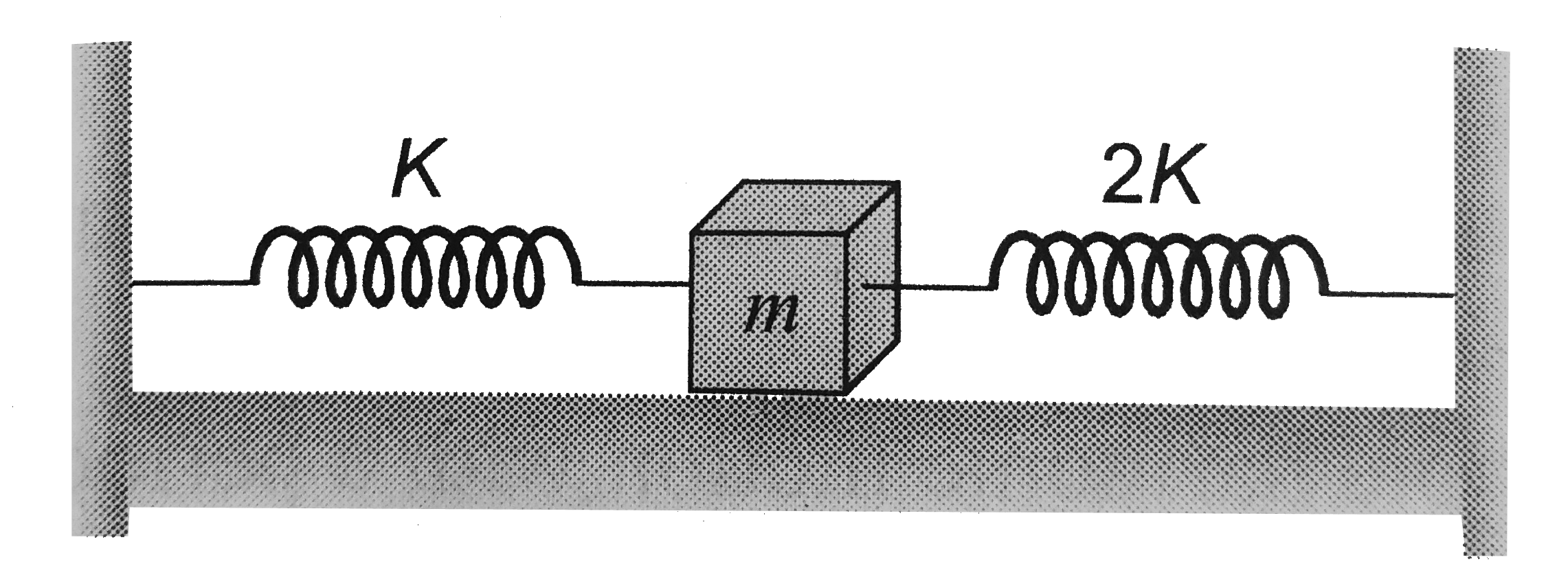
View SolutionSprings of spring constans K, 2K, 4K, 8K,….2048 K are connected in series. A mass .m. is attached to one end the system is allowed to oscillation. The time period is approximately
View SolutionSprings of spring constants K, 2K, 4K, 8k, .... 2048 K are connected in series. A mass 'm' is attached to one end the system is allowed to oscillation. The time period is approximately
View SolutionSprings of spring constans K, 2K, 4K, 8K,….2048 K are connected in series. A mass .m. is attached to one end the system is allowed to oscillation. The time period is approximately
View SolutionThe period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionA spring of spring constant k is cut into n equal parts, out of which r parts are placed in parallel and connected with mass M as shown in figure. The time period of oscillatory motion of mass M is:
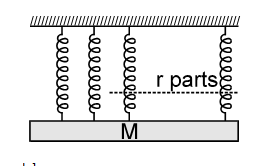
View SolutionA spring of spring constant k is cut into n equal parts, out of which r parts are placed in parallel and connected with mass M as shown in figure. The time period of oscillatory motion of mass M is:
View SolutionSprings of constants k, 2k, 4k, 8k,…….,2048k are connected in series. A mass m is attached to one end and the system is allowed to oscillate. The time period is approximately
View SolutionA load of mass 'M' is attached to the bottom of a spring of mass and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
View SolutionA load of mass .M. is attached to the bottom of a spring of mass .M/3. and spring constant .K.. If the system is set into oscillation, the time period of oscillation is
View SolutionA load of mass .M. is attached to the bottom of a spring of mass .M/3. and spring constant .K.. If the system is set into oscillation, the time period of oscillation is
View SolutionA local of mass 'M' is attached to the bottom of a spring of mass M"/"3 and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
View SolutionA load of mass M is attached to the bottom of a spring of mass M/3 and spring constnat K. If the system is set into oscillation, the time period of oscillation is
View SolutionA load of mass is attached to the bottom of a spring of mass and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
View SolutionTwo indentical springs each of force constant k are connected in paralle and they support a mass m. Calculate the time period of the system
View Solution