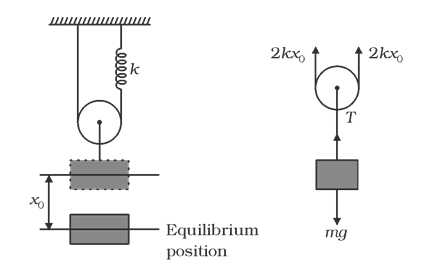
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.

2π√mk
π√mk
4π√mk
2π√m2k
The correct Answer is:B
When the block is displaced by x0. The spring gets elongated by 2xo.Since pulley is massles, tension, T=4kxo
If the whole set - up is replaceds by a single spring -bloick, then the equivalent spring will be keqxo=mgkeq=4k
therefore Time period, T=2π√mkeq=2π√m4k=π√mk
Similar Questions
Find the time period of the oscilltion of mass m in figure a and b. What is the equivalent spring constant of the spring in each case. ?

View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
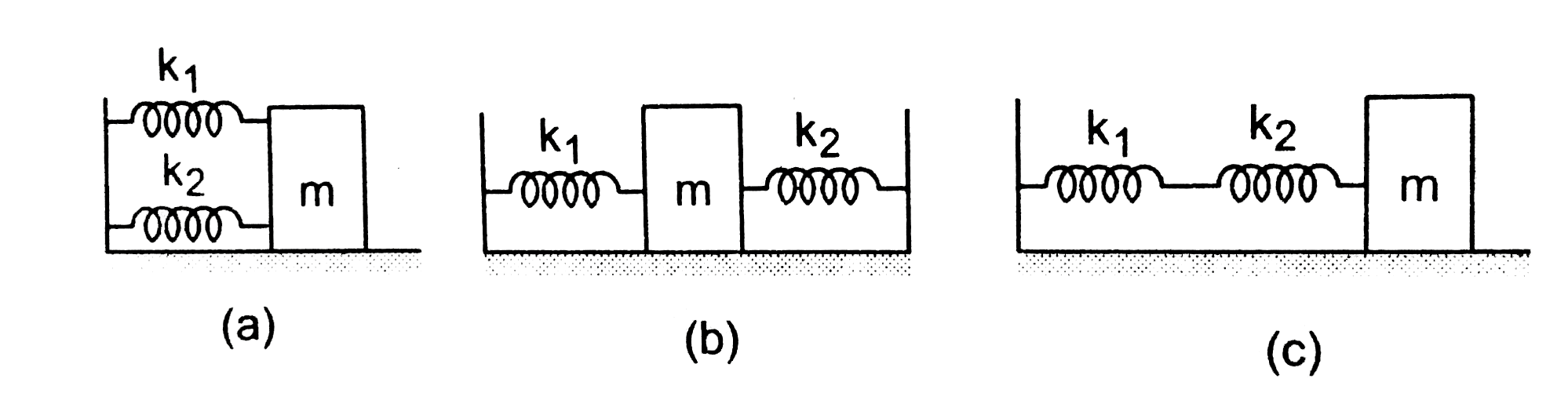
View Solution
Knowledge Check
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
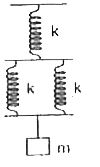 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
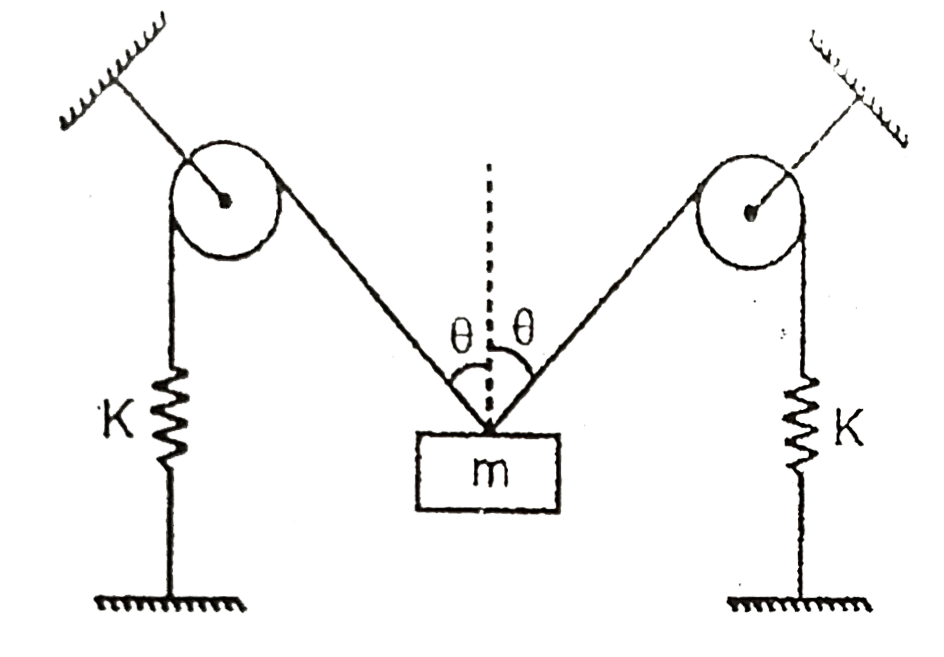 A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2kThe time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
A0.2πsB0.21πsC0.22πsD0.02πs
The pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.

View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionThe time period of oscillations of a block attached to a spring is t1. When the spring is replaced by another spring, the time period of the block is t2. If both the springs are connected in series and the block is made to oscillate using the combination, then the time period of the block is
View SolutionA bar of mass m is suspended horizontally on two vertical springs of spring constant k and 3k. The bar bounces up and down while remaining horizontal. Find the time period of oscillation of the bar neglect mass of springs and friction everywhere
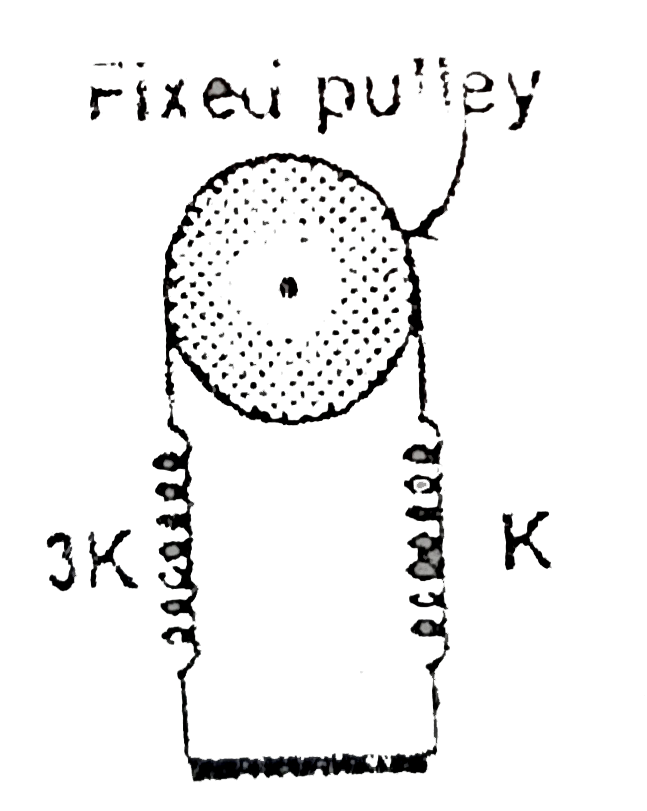
View Solution